15. Декартовы координаты на плоскости. Определение, простейшие задачи ( нахождение расстояние

между точками, деление отрезка в заданном отношении)

Декартовы координаты на плоскости

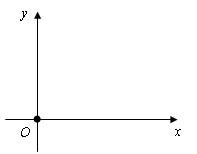  У нас есть две прямые x и y, которые пересекаются в точке O. Эти прямые называются осями координат. Ось x называется осью абсцисс, а ось y – осью ординат. Точка пересечения осей называется началом координат. Каждая ось разбивает плоскость на две полуплоскости, одна из них положительная, другая отрицательная.  Будем обозначать плоскость Oxy (O - точка пересечения оси x с осью y). 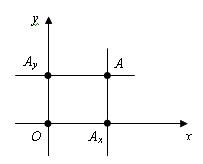   Любой точки плоскости, допустим точки A, можно сопоставить пару чисел, эта пара чисел называется координатами точки. Они определяются так:  1) проведем через точку A прямую, параллельную оси ординат. Эта прямая пересечет ось абсцисс x в некоторой точке Ax . Число x, абсолютная величина которого равна расстоянию от точки O до точки Ax , называется абсциссой точки A.  2) проведем через точку A прямую, параллельную оси абсцисс. Эта прямая пересечет ось ординат x в некоторой точке Ax. Число y, абсолютная величина которого равна расстоянию от точки O до точки Ay, называется ординатой точки A.  Если Ax принадлежит положительной полуоси, то это положительно число, если отрицательной – отрицательное число.  Если Ay принадлежит положительной полуоси, то это положительно число, если отрицательной – отрицательное число.  Если точка A лежит на оси ординат y, то x=0.  Если точка A лежит на оси абсцисс x, то y=0.  Координаты точки A записываются так: A (x; y). 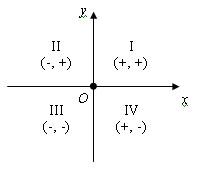   Плоскость разбивается координатными осями на четыре части – четверти: I, II, III и IV. В пределах одной четверти знаки обеих координат сохраняются и имеют значения, как на рисунке.  Введенные на плоскости координаты x и y называются декартовыми координатами.

Примеры задач:

Найти расстояние между точками A(4, -5) и B(7, -1).

Решение.

По формуле

для расстояния d между двумя точками, если взять в ней x₁ = 4; x₂ = 7; y₁ = -5; y₂ = -1, получаем

d = 5 единиц масштаба.

Если точка М(x; y) лежит на прямой, проходящей через две данные точки (, ) и (, ), и дано отношение , в котором точка М делит отрезок , то координаты точки М определяются по формулам

, .

Если точка М является серединой отрезка , то ее координаты определяются по формулам

, .

16. Полярные координаты, связь между декартовыми и полярными координатами точки

Полярные координаты

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Полярными координатами произвольной точки М (относительно заданной системы) называются числа  и (см. рис.). Угол  при этом следует понимать так, как принято в тригонометрии. Число  называется первой координатой, или полярным углом точки М ( называются также амплитудой).

Символ М(; ) обозначает, что точка М имеет полярные координаты  и .

Полярный угол  имеет бесконечно много возможных значений (отличающихся друг от друга на величину вида , где n - целое положительное число). Значение полярного угла, удовлетворяющее неравенствам , называется главным.

В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1). Пользоваться одним и тем же масштабом, 2). При определении полярных углов считать положительным повороты в том направлении, в каком следует вращать положительную ось абсцисс, чтобы кратчайшим путем совместить ее с положительной осью ординат (таким образом, если оси декартовой системы находятся в обычном расположении, то есть ось Ох направлена вправо, а ось Оу - вверх, то и отсчет полярных углов должен быть обычным, то есть положительными следует считать те углы, которые отсчитываются против часовой стрелки).

При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки х к декартовым координатам той же точки осуществляется по формулам

, .

В этом же случае формулы

, 

являются формулами перехода от декартовых координат к полярным.

При одновременно рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштаб для обеих систем одинаковыми.