7.5. Методика изучения квадратичной функции

Изучение функции в школе состоит из основных трех частей:

- изучение понятия функция и способов ее задания;

- исследование функции элементарными средствами;

- изучение начал математического анализа их применение к исследованию функций средствами дифференциального исчисления.

Свойства функции в основной школе устанавливаются по графику, на основе наглядных соображений и соответствующих приемов. Перечень свойств, подлежащих рассмотрению, увеличивается постепенно по мере овладения учащимися соответствующим теоретическим материалом.

Уровень требований к объему и глубине знаний учащихся о функциях постепенно повышается. Они учатся исследовать функцию на трех «языках»: графическом, словесном и символическом.

В 10 классе повторяются и обобщаются общие сведения о функциях. Основным понятиям – «числовая функция» и «способ задания числовой функции» - даются более точные определения и обозначения, уточняются определения всех основных свойств функций и приемов их выявления элементарными средствами при сохранении графической интерпретации, появляется задача построения графика функции на основе ее исследования.

7.5.1. Определение квадратичной функции и ее свойства

Практически во всех учебниках изучение данной темы начинается с введения определения квадратичной функции.

Определение. Квадратичной функцией называется функция, которую можно задать формулой вида , где- независимая переменная,некоторые числа, причём.

Изучение квадратичной функции происходит в следующей последовательности:

1), где(график - парабола);

2), где.

Предлагается рассмотреть следующие функции:, которые обладают теми же свойствами, что и функция, а их графики строятся с использованием некоторых преобразований.

3) . Учащиеся усваивают, что график данной функции может быть получен из графика функциис помощью симметрии относительно осих.

4) . Решая квадратное уравнение, учащиеся находятся его корни.

5) ,. Учащиеся усваивают, что- вершина параболы.

6) , если. Вводится понятие квадратичной функции.

Свойства квадратичной функции, если a>0

1) , так как значение квадратного трехчлена однозначно определено для любого действительного числа.

2) Убывает на луче (], возрастает на луче [)

у(х₁) – у(х₂) =…=а(х₁ – х₂) ((х₁ – х₀) + (х₂ – х₀)). Имеем а> 0, х₁ > х₂ х_0. Тогда все три сомножителя в полученном выражении положительны. Это означает, что у(х₁) – у(х₂) > 0 , при а> 0 квадратичная функция является возрастающей на промежутке .

3) Точки пересечения с осями координат.

Если х = 0, то получим точку с координатами (0;с).

Если Д = 0, то - (х₀; 0).

Если Д<0, то точек пересечения с осью абсцисс нет.

Если Д>0, то квадратное уравнение имеет два корня, которые вычисляются по формуле. Поэтому существует две точки пересечения с осью абсцисс, они имеют координаты (х₁;0), (х₂;0).

4) Ограничена снизу, не ограничена сверху.

5) не существует.

6) Функция непрерывна (дается поясняющее описание);

7) [)

Доказательство. Преобразуем квадратный трехчлен, выделив полный квадрат.

у = ах² + вх + с = а(х² + в/а х + с/а) = а ((х + в/2а)² - ) = а(х –х₀)² + у₀, где использованы обозначения, ,. Выражение (х –х₀)² может принимать любое неотрицательное значение в зависимости от х. Поэтому областью значений выражения а(х –х₀)² + у₀ при всех действительных х является [).

8) Выпуклая вниз (первичное знакомство).

Аналогично рассматриваются свойства функции, если а < 0.

Вводится понятие «график функции».

Графиком функции является парабола с вершиной в точке, где,, и с ветвями, направленными вверх, еслиa>0, и вниз, если a<0. Прямая - является осью параболы.

Следует обратить внимание на алгоритм построения параболы, предложенный в учебнике А.Г. Мордковича.

1. Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось параболы.

2. Отметить на оси 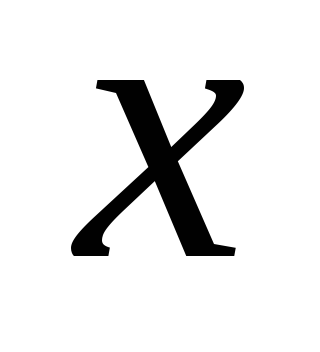две точки, симметричные относительно оси параболы (чаще всего в качестве одной из таких точек берут точку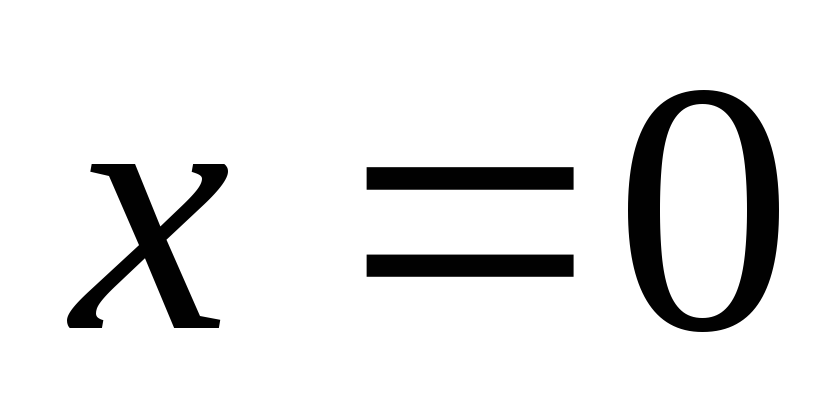), найти значения функции в этих точках; построить на координатной плоскости соответствующие точки.

3. Через полученные три точки провести параболу (в случае необходимости надо взять ещё пару точек, симметричных относительно оси параболы, и построить параболу по пяти точкам).

В упражнениях предлагаются задания: построить графики функций, найти наибольшее и наименьшее значения, указать промежутки возрастания и убывания функции; по графику функции определить, какой функции он соответствует, и перечислить свойства данной функции.