Третьяков

Министерство Образования Российской Федерации

Саратовский Государственный Технический Университет

Международный Факультет прикладных Информационных Технологий

Разработка имитационной модели для прогнозирования спроса автомобилей в автосалоне

Подготовил: студент МФПИТ группы ПИН-41

Третьяков А.

Проверил:

Костюк В.П.

Саратов 2012

Цель разработки

Целью данной работы является разработка имитационной модели для автосалона «Третьяков и К», с целью прогноза спроса автомобилей.

Модель будет разработана через статистику предыдущих продаж.

Построение данной модели позволит в дальнейшем спрогнозировать количество автомобилей, спрос на которых высок и наиболее рационально делать закупку авто.

Описание объекта

Автосалон занимается продажами отечественного авто, таких моделей как Лада Гранта, Лада Калина, Приора, 2113, 2114, 2115.

Схема БД для поддержки работы автосалона

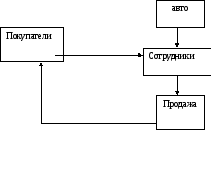
Цель моделирования

Повышение прибыли автосалона на основе увеличения закупки авто, спрос на которые повышен.

Чтобы достигнуть данной цели, необходимо решить следующие задачи:

1. Собрать статистику по количеству проданных авто для моделирования из имеющейся базы данных.

2. Построить нейрокомпьютерную модель

3. Обучение построенной модели

4. Проведение эксперимента на основе обученной модели

5. Обработка результатов. Построение прогноза.

Данными, необходимыми для разработки модели являются:

1. Месяц

2. Количество продаж авто.

Общий алгоритм моделирования

БД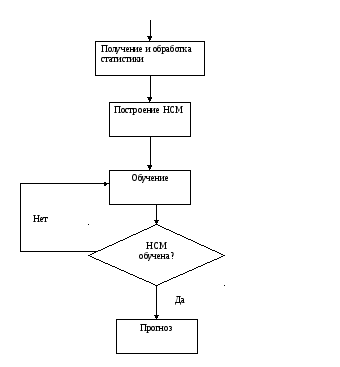

Он осуществляется следующим образом: из имеющейся базы данных мы получаем статистику проданных авто. Строим нейрокомпьютерную модель.

Для обучения НСМ необходимо построить входные вектора X={X_i/i=1,7}, где X_j={x_n/n=1,N}, N=const, где

X_n=1 – количества проданных авто за первый месяц;

X_n=2 – количества проданных авто за второй месяц;

X_n=3 – количества проданных авто за третий месяц;

X_n=4 – количества проданных авто за четвертый месяц;

X_n=5 – количества проданных авто за пятый месяц;

X_n=6 – количества проданных авто за шестой месяц

X_n=7 – количества проданных авто за седьмой месяц

В базе данных будет храниться статистика за 7 месяцев.

Схема обучения следующая: берем статистику за первый месяц и будем обучать НСМ на последующий месяц. Это будет выглядеть следующим образом:

Входной слой выходной слой

Х1

--

Х4

Х5

Х6

Х7 1

Таким образом, наша нейронная сеть будет иметь следующие слои:

1. Входной слой – количество проданных авто

2. Выходной слой нейронов

Алгоритм обучения

Для реализации данной модели будет использоваться обучение методом обратного распространения.

В данном методе используется функция

OUT=1/1+e^-NET, которая хорошо дифференцируется: ∂OUT/∂NET=OUT(1-OUT), где NET – взвешенная сумма входов нейрона, OUT – сигнал, который получается из суммы NET, которая модифицируется с помощью активационной функции.

Обратное распространение применимо к сетям с любым числом слоев и обладает преимуществом прямого поиска, т.е. веса всегда корректируются в направлении, минимизирующем функцию ошибки.

Обучение сети обратного распространения требует выполнения следующих операций:

1. Выбрать очередную обучающую пару из обучающего множества, подать входной вектор на вход сети.

2. Вычислить выход сети

3. Вычислить разность между входом сети и требуемым выходом (целевым вектором обучающей пары).

4. Подкорректировать веса сети так, чтобы минимизировать ошибку

5. Повторять шаги с 1 по 4 для каждого вектора обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого уровня.

Операции, выполняемые шагами 1 и 2, сходны с теми, которые выполняются при функционировании уже обученной сети, т.е. подается входной вектор и вычисляется получающийся выход. Вычисления выполняются послойно.

После достаточного числа повторений этих четырех шагов, разность между действительными выходами и целевыми выходами должна уменьшиться до приемлемой величины, при этом говорят, что сеть обучилась. Теперь сеть используется для распознавания и веса не изменяются.

1) случайным образом подбираем веса:

W11=0,6 W21=0,3 W31=0,2

W12=0,1 W22=0,7 W32=0,6

W13=0,02 W23=0,01 W33=0,8

… … …

2) Считаем величину NET – взвешенная сумма входов нейрона по формуле:

NET=∑x_iw_i

NET₁=0,3*0,6+0,9*0,1+0,4*0,2…=0,35

NET₂=0,3*0,3+0,9*0,7+0,4*0,01…=0,7

NET₃=0,3*0,2+0,9*0,6+0,4*0,8…=0,9

3) Считаем OUT по формуле:

OUT=1/(1+e^-net)

OUT₁=1/1+2,7^-0,35=0,6

OUT₂=1/1+2,7^-0,7=0,67

OUT₃=1/1+2,7^-0,9=0,7

Снова подберем веса:

W41=0,3

W42=0,2

W43=0,9

…

NET₄=OUT₁* W41+ OUT₂* W42+ OUT₃* W43=0,6*0,3+0,67*0,2+0,7*0,9=0,9

OUT₄=1/1+2,7^-0,9=0,5

4) Вычитаем сигнал ошибки. Он будет рассчитан по формуле:

∂=OUT(1-OUT)(TARGET-OUT)=0,7(1-0,7)(0,4-0,7)= -0,063

5)∆w=µ∂OUT, где

µ - скорость обучения (обычно от 0,01 до 1,0)

µ=0,05

∆w – величина веса от нейрона в скрытом слое, к нейрону в выходном слое на шаге n (до коррекции).

∆w=0,05*(-0,063)*0,7= -0,002

W51=W41+∆w=0,3-0,002=0,3

W52=0,2

W53=0,89

NET₅= OUT₁* W51+ OUT₂* W52+ OUT₃* W53=0,94

OUT₅=1/(1+e^-net)=0,78

Разница между действительными выходами и желаемыми выходами стала меньше, это значит, что мы стали ближе к желаемому результату.

После достаточного числа повторений этих действий, разность между действительными входами и желаемыми выходами должна уменьшиться до приемлемой величины, это значит, что сеть обучилась.

Реализация модели

Для реализации обучения модели с помощью алгоритма обратного распределения было использовано программное средство Visual Studio 2010.

Программный код можно разделить на несколько смысловых частей. Эти смысловые части выполняются последовательно, они могут повторяться множество раз, пока мы не достигнем желаемого результата, т.е. мы должны на выходе получить значения как можно ближе к эталону:

• Выбор процесса для прогнозирования (количество проданных авто);

• Извлечение данных из базы данных;

• Масштабирование входных векторов (каждый элемент массива масштабируется в диапазоне от 0 до 1);

• Задание весовых коэффициентов случайным образом ;

• Расчет выходных нейронов;

• Расчет значения на выходе сети;

• Сопоставление реального и желаемого результатов;

• Определение ошибки;

• Минимизация ошибки путём настраивания весовых коэффициэнтов.

Значение, получаемое на выходе, стремиться к эталону – желаемому результату. Выход из цикла произойдет тогда, когда таким образом будут перебраны все значения из базы данных. Результаты обучения на каком-то конкретном этапе могут быть сохранены.

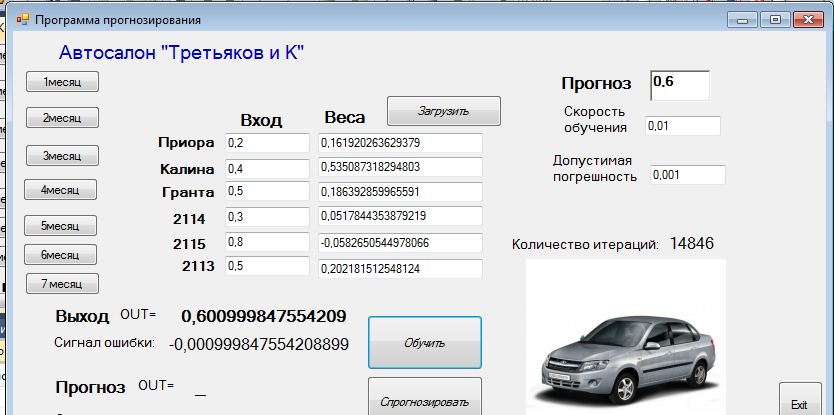
На основе данной модели было произведено несколько попыток обучения. Как наиболее оптимальное решение, было принято значение скорости обучения 0,01 и допустимый уровень погрешности 0,001.

В итоге было осуществлено полное обучение нейронной сети, и были получены прогнозы на заданный период времени.

Программное решение

Решение поставленной задачи реализовано в программной среде Visual Basic 2010. Выбор данной программы обуславливается её простотой, актуальностью, а также наличием опыта работы в данной среде.

Интерфейс:

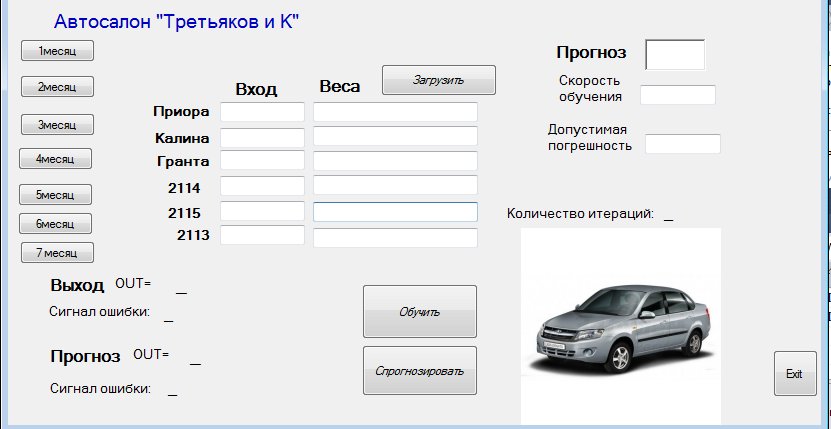
Вывод

В ходе работы были сделаны следующие выводы:

• Чем меньше ошибка, тем точнее результаты обучения;

• Чем больше скорость обучения, тем менее точны результаты обучения.

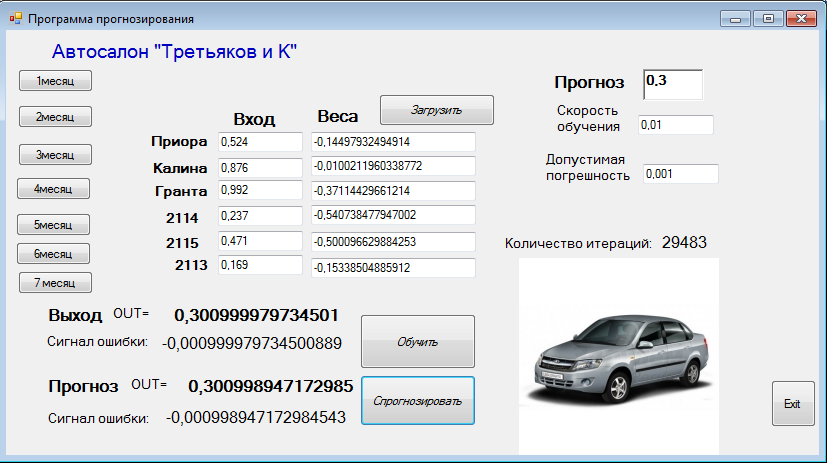
В итоге получилось, что на 8 месяц прогноз спроса составляет 0,3 :

Скорость обучения – 0,01,

сигнал ошибки – 0,001.

Погрешность составляет 60%.

Обучение нейросети выполнено за 29483 итераций.