§ 8. Отображение множеств. Обратное отображение. Композиция отображений. Понятие действительной функции

Понятие отображения множеств играет важную роль во всех областях математики.

Определение 1. ПустьХ иY– некоторые множества и. Если каждому элементупоставлен в соответствие один и только один элемент, то говорят, что заданоотображение из Х в Y с областью задания А.

Отображения обычно обозначают малыми латинскими буквами .

Пример 1. ПустьХ – множество натуральных чисел,. Каждому числупоставим в соответствие остаток от его деления на 2:. Получим отображение изХ в множество действительных чиселR, при котором каждому соответствует либо 0, либо 1.

Множество Х называют такжемножеством отправления, а множествоY –множеством прибытия.

Определение 2. Элемент, соответствующий элементув отображенииf, называетсяобразом элементах и обозначается. При этом сам элементх называетсяпрообразом элементау. ЕслиА– область задания при отображенииf, то множествоназываютобразом множества А при отображенииf илиобластью значений отображенияf.

Определение 3. Если область задания совпадает с областью отправления, т.е, тоf называют отображением Х вYобозначают. Если, тоf называют отображениемХ наY.

Определение 4. Отображениеназываетсяобратимым, если разным элементамсоответствуют различные элементы, т.е. для любыхимеем.

Например, отображение с областью заданияR не является обратимым, так каки, т.е., хотя.

Определение 5. Обратимое отображениеХ наY называетсявзаимно однозначным отображением.

Введенные понятия проиллюстрируем рисунками.

f не является отображением

д)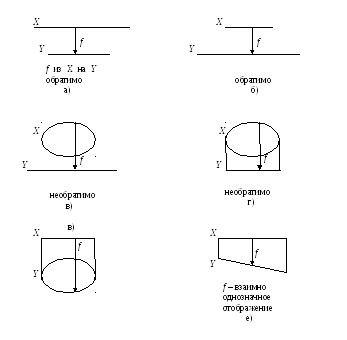

Пусть f – обратимое отображение изХ вY с областью заданияА. Тогда каждому элементусоответствует один и только один элемент, причем разным элементамсоответствуют различные элементыу. Поэтому определено отображениемножествавХ(наА). Определено так, что.

Определение 6. Если отображениеfизХ вY обратимо, то отображениеизY вХ, определяемое соотношением, называетсяобратным к f.

Пусть теперь f– отображениеХвY, аg– отображениеY вZ. Определим отображениеХ вZ следующим образом:. Таким образом,, то есть. Такое отображение называетсякомпозицией отображенийf иgи обозначается. Итак, для всех

.

Операция композиции отображений обладает следующими свойствами.

1. Ассоциативность:

.

Действительно, если , то

и .

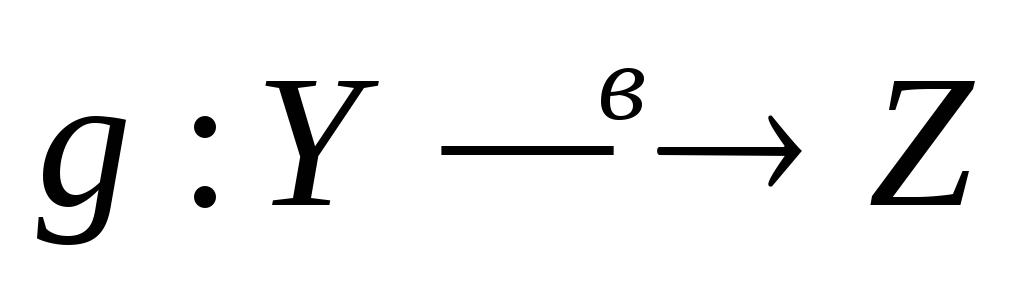2. Если отображения иобратимы, то и их композиции обратима, причем

.

Действительно, пусть и. В силу обратимостиf . В силу обратимостиg и, значит, отображениеобратимо. Если, то, а, то есть, что и требовалось доказать.

Действительная функция есть частный случай отображения, когда множества X иYявляются числовыми множествами.

Определение 7. ПустьX – числовое множество. Отображение, сопоставляющее каждому числучисло, называетсядействительной функцией, заданной на множествеХ. При этомхназываетсяаргументомфункцииf,Х–областью ее определения,–значениемфункции. Множествоназываетсямножеством значенийфункции.

Определение 8. Если функцияf ставит в соответствие каждому числуодно и то же значениеа, то функциюf называютпостоянной.

Из определения действительной функции следует, что для задания функции f надо задать ее область определения – множествоХи закон, по которому каждому числуставится в соответствие число.

В зависимости от того, каким образом задается закон функциональной зависимости, различают несколько способов задания функции.

Аналитический способ. Закон функциональной зависимости задается с помощью формулы, указывающей, какие действия нужно произвести над аргументомх, чтобы получить значение функции.

Примеры: и т.д.

В случае аналитического способа задания функции множество Хчасто не указывают. Областью определения функции в этом случае считаютестественную область определения функции – множество значений аргумента, для которых имеет смысл данное аналитической выражение.

Например, для функции область определения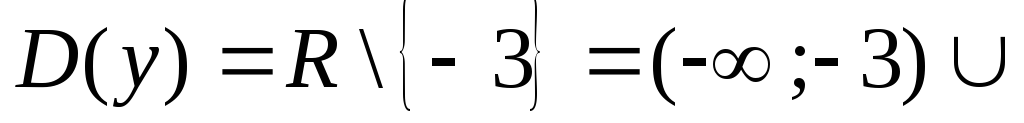, для функции.

Если функция отражает зависимость между конкретными величинами (физическими, геометрическими и другими), то область ее определения может не совпадать с той областью, где формула имеет смысл. Например, функция , рассматриваемая абстрактно, определена наR, если же она выражает закон свободного падения тела, то.

Заметим, что функция может быть задана не одной, а несколькими формулами.

Например, 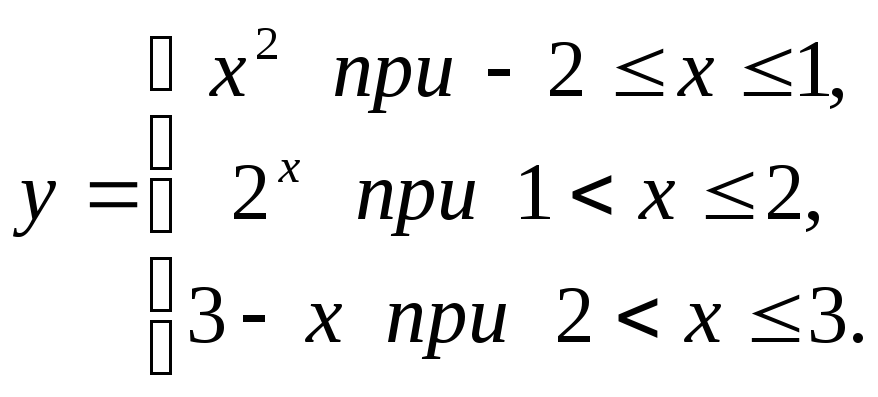Для этой функции.

Табличный способ. При этом способе задания закон функциональной зависимости устанавливается таблицей, в которой различным значениям аргумента сопоставлены соответствующие значения функции.

Табличный способ используется в экспериментальных исследованиях, когда, например, снимаются показания приборов через определенные промежутки времени.

Составлены таблицы значений многих функций, часто применяемых при технических расчетах, которые позволяют находить значения функций без вычислений.

Недостаток табличного способа состоит в том, что по таблице можно найти значения функции только для тех значений аргумента, которые в ней есть. Другие значения можно находить с помощью интерполирования приближенно.

Графический способ.

Определение 9.Графиком функции, заданной на множествеХ, называется множество всех точек плоскости, координаты которыххиусвязаны соотношением. Равенствоназываетсяуравнением этого графика.

Функция считается заданной графически, если начерчен ее график. Например, для измерения давления атмосферы на различных высотах используется специальный самопишущий аппарат – барограф, который на движущейся ленте записывает в виде кривой изменение давления в зависимости от высоты.

Не всякая кривая может служить графиком некоторой функции. Необходимо, чтобы не содержалось на ней никаких двух точек с одинаковыми абсциссами.

х

у

О

х

у

О

Кривая определяет Кривая не определяет

функцию никакой функции

Преимущество графического способа задания функции перед другими – в наглядности, недостаток в том, что значения функции можно найти лишь приближенно. Не для всякой функции можно построить график. Например, нельзя изобразить графически функцию Дирихле (Петер Густав Лежен-Дирихле (1805-1859) – немецкий математик)

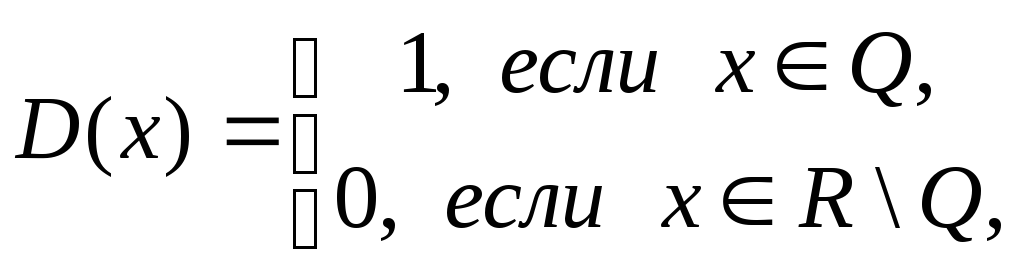
так как между любыми двумя значениями х имеется бесконечно много как рациональных, так и иррациональных точек.

Словесный способ. Функция задается словами. Например, целая часть числах– это наибольшее целое число, не превосходящеех.

Определение 10. Функциии, заданные на некотором промежуткеХ, называютсятождественно равными на этом промежутке:, если их значения в каждой точкесовпадают.

Пример. Тождественны ли функции:

1) и;

2) идля;

3) и?

Решение. 1), т.е., т.е. функции тождественно равны.

2) по свойству.

3) , т.е., функции не являются тождественно равными.