
- •Глава 1. Введение в математический анализ
- •§ 1. Множество r действительных чисел и его свойства
- •§ 2. Числовые множества, их границы
- •§ 3. Абсолютная величина числа
- •§ 4. Понятие числовой последовательности. Бесконечно большая и бесконечно малая последовательности, их свойства
- •§ 5. Сходящиеся последовательности, их свойства
- •§ 6. Монотонные последовательности. Число е
- •§ 7. Теорема Больцано-Вейерштрасса. Принцип сходимости
- •§ 8. Отображение множеств. Обратное отображение. Композиция отображений. Понятие действительной функции
- •§ 9. Арифметические операции над функциями. Композиция функций
- •§ 10. Ограниченные и неограниченные функции. Монотонные функции
- •§ 11. Четные и нечетные функции. Периодические функции
- •§ 12. Обратная функция
§ 3. Абсолютная величина числа
Определение.Абсолютной величиной(илимодулем) действительного
числа![]() (обозначается
(обозначается![]() )
называется неотрицательное число,
удовлетворяющее условиям:
)
называется неотрицательное число,
удовлетворяющее условиям:
![]()
Ясно, что всегда
![]() .
(3.1)
.
(3.1)
Свойства абсолютных величин:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
Доказательство.1) Если![]() ,
то
,
то![]() в силу (3.1). Если
в силу (3.1). Если![]() ,
то
,
то![]() .
Первое свойство доказано.
.
Первое свойство доказано.
2) Имеем
![]() ,
отсюда
,
отсюда![]() .
Второе свойство доказано.
.
Второе свойство доказано.
3)
![]() ,
третье свойство доказано.
,
третье свойство доказано.
Четвертое свойство доказывается так же, как свойство 3).
Замечание. Свойство 1) распространяется на любое число слагаемых, свойство 3) – на любое число сомножителей.
Отметим также, что
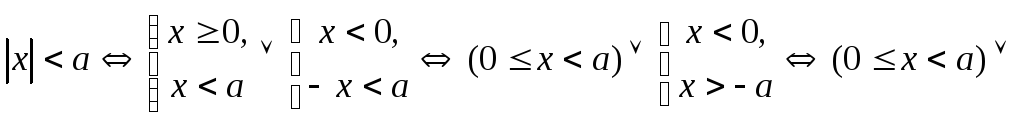
![]() ,
т.е.худовлетворяет неравенству
,
т.е.худовлетворяет неравенству![]() тогда и только тогда, когда принадлежит
интервалу
тогда и только тогда, когда принадлежит
интервалу![]() .
.
Геометрический смысл модуля действительного
числа состоит в том, что
![]() равен расстоянию от точкихна
числовой прямой до нуля.
равен расстоянию от точкихна
числовой прямой до нуля.
§ 4. Понятие числовой последовательности. Бесконечно большая и бесконечно малая последовательности, их свойства
Определение 1. Если каждому значениюn из множества
натуральных чисел![]() ставится в соответствие по определенному
закону некоторое действительное число
ставится в соответствие по определенному
закону некоторое действительное число![]() ,
то множество занумерованных действительных
чисел называетсячисловой
последовательностью
,
то множество занумерованных действительных
чисел называетсячисловой
последовательностью ![]() .
.
![]() – члены последовательности,
– члены последовательности,![]() –
сокращенная запись последовательности.
Например,
–
сокращенная запись последовательности.
Например,![]() .
.
Определение 2. Пусть даны две
последовательности![]() и
и![]() .
Последовательности
.
Последовательности![]() называются соответственно суммой,
разностью, произведением и частным
последовательностей
называются соответственно суммой,
разностью, произведением и частным
последовательностей![]() и
и![]() .
.
Определение 3. Последовательность![]() называетсяограниченной, если
множество ее членов ограничено, т.е.
существует число
называетсяограниченной, если
множество ее членов ограничено, т.е.
существует число![]() ,
такое, что
,
такое, что![]() .
Последовательность
.
Последовательность![]() называетсяограниченной сверху
(снизу), если существует
числоМ, такое, что
называетсяограниченной сверху
(снизу), если существует
числоМ, такое, что![]() .
.
Если последовательность
![]() неограниченна, то для любого числа
неограниченна, то для любого числа![]() найдется номерnтакой, что
найдется номерnтакой, что![]() .
Ясно, что если последовательность
ограничена только снизу или только
сверху, то она неограниченна. Среди
неограниченных последовательностей
выберем бесконечно большие
последовательности.
.
Ясно, что если последовательность
ограничена только снизу или только
сверху, то она неограниченна. Среди
неограниченных последовательностей
выберем бесконечно большие
последовательности.
Определение 4. Последовательность![]() называетсябесконечно большой,
если для любого
называетсябесконечно большой,
если для любого![]() найдется номерN,
такой, что
найдется номерN,
такой, что![]() для всех
для всех![]() .
.
Всякая бесконечно большая последовательность
неограниченна, но не всякая неограниченная
последовательность бесконечно большая.
Примером этого может служить
последовательность
![]() .
.
Определение 5. Последовательность![]() называетсябесконечно малой,
если для любого
называетсябесконечно малой,
если для любого![]() найдется номерN,
такой, что
найдется номерN,
такой, что![]() для всех
для всех![]() .
.
Установим основные свойства бесконечно малых последовательностей.
Теорема 1. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть![]() и
и![]() – бесконечно малые последовательности.
Возьмем
– бесконечно малые последовательности.
Возьмем![]() произвольно и положим
произвольно и положим![]() .
По определению 5 для
.
По определению 5 для![]() найдутся номера
найдутся номера![]() и
и![]() ,
такие, что
,
такие, что![]() для всех
для всех![]() и
и![]() для всех
для всех![]() .
Положим
.
Положим![]() .
Тогда для всех
.
Тогда для всех![]()
![]() и по определению 5 последовательность
и по определению 5 последовательность![]() бесконечно
малая. Теорема доказана.
бесконечно
малая. Теорема доказана.
Аналогично доказываются
Теорема 2. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 3. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
(Можно поручить студентам доказать теоремы 2, 3 и следствие самостоятельно).
Теорема 4. Всякая бесконечно малая последовательность ограничена.
Доказательство. Пусть![]() – бесконечно малая последовательность.
Положим
– бесконечно малая последовательность.
Положим![]() .
По определению 5 найдется номерN,
такой, что
.
По определению 5 найдется номерN,
такой, что![]() для всех
для всех![]() .
Обозначим
.
Обозначим![]() .
Тогда
.
Тогда![]() для всехn. Теорема
доказана.
для всехn. Теорема
доказана.
Следствие теорем 3и 4. Произведение двух (любого конечного числа) бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 5. Если все члены бесконечно
малой последовательности равны одному
и тому же числус, то![]() .
.
Доказательство. Предположим
противное, т.е. что![]() .
Возьмем
.
Возьмем![]() .
По определению 5 найдется номерN,
такой, что
.
По определению 5 найдется номерN,
такой, что![]() для всех
для всех![]() ,
т.е.
,
т.е.![]() для всех
для всех![]() ,
а этого не может быть, так как
,
а этого не может быть, так как![]() для всехn. Противоречие
доказывает утверждение теоремы.
для всехn. Противоречие
доказывает утверждение теоремы.
Теорема 6. Если![]() – бесконечно большая последовательность,
то
– бесконечно большая последовательность,
то![]() –
бесконечно малая последовательность.
–
бесконечно малая последовательность.
Доказательство. Возьмем![]() произвольно и положим
произвольно и положим![]() .
Тогда по определению 4 найдется номерN, такой, что
.
Тогда по определению 4 найдется номерN, такой, что![]() для всех значений
для всех значений![]() .
Отсюда
.
Отсюда![]() для всех
для всех![]() ,
т.е.
,
т.е.![]() –
бесконечно малая последовательность
по определению 5. Теорема доказана.
–
бесконечно малая последовательность
по определению 5. Теорема доказана.
Теорема 7. Если![]() –
бесконечно малая последовательность
и все члены этой последовательности
отличны от нуля, то последовательность
–
бесконечно малая последовательность
и все члены этой последовательности
отличны от нуля, то последовательность![]() –
бесконечно большая (доказать
самостоятельно).
–
бесконечно большая (доказать
самостоятельно).
