
- •Глава 2. Дифференциальное исчисление функций одной и нескольких переменных
- •§ 1. Определение производной. Ее механический и геометрический смысл. Уравнения касательной и нормали к кривой
- •§ 2. Дифференцируемые функции. Непрерывность дифференцируемой функции. Производная сложной функции
- •§ 3. Правила дифференцирования. Производные основных элементарных функций
- •§ 4. Дифференциал функции, его вычисление
- •§ 5. Производные и дифференциалы высших порядков
- •§ 6. Основные теоремы о дифференцируемых функциях
- •§ 7. Правило Лопиталя раскрытия неопределенностей
§ 4. Дифференциал функции, его вычисление
Рассмотрим дифференцируемую в точке
![]() функцию
функцию![]() .
Ее приращение в этой точке имеет вид
(см. (2.1))
.
Ее приращение в этой точке имеет вид
(см. (2.1))
![]() ,
,
где
![]() и не зависит от
и не зависит от![]() ,
а
,
а![]() при
при![]() .
Заметим, что если
.
Заметим, что если![]() ,
то слагаемое
,
то слагаемое![]() имеет тот же порядок, что и
имеет тот же порядок, что и![]() ,
и линейно относительно
,
и линейно относительно![]() ,
а слагаемое
,
а слагаемое![]() имеет порядок, высший по отношению к
имеет порядок, высший по отношению к![]() .
Поэтому слагаемое
.
Поэтому слагаемое![]() есть главная часть приращения
есть главная часть приращения![]() .
.
Определение 1. Главная, линейная
относительно![]() ,
часть приращения
,
часть приращения![]() функции
функции![]() называетсядифференциалом этой
функции и обозначается
называетсядифференциалом этой
функции и обозначается![]() или
или![]() .
.
Таким образом,
![]() ,
,
где
![]() и от
и от![]() не зависит.
не зависит.
Как было показано в теореме 1 § 2
![]() ,
поэтому
,
поэтому
![]() .
(4.1)
.
(4.1)
Формула (4.1) справедлива и для функции
![]() ,
поэтому
,
поэтому![]() или
или![]() .
Учитывая это, равенство (4.1) можно
записать в виде
.
Учитывая это, равенство (4.1) можно
записать в виде
![]() .
(4.2)
.
(4.2)
Из (4.2) имеем
![]() ,
,
т.е. производную можно рассматривать как частное от деления дифференциала функции на дифференциал аргумента.
Поскольку
![]() отличается от
отличается от![]() на величину
на величину![]() ,
стремящуюся к нулю при
,
стремящуюся к нулю при![]() ,
разность
,
разность![]() можно сделать сколь угодно малой, взяв
достаточно малое
можно сделать сколь угодно малой, взяв
достаточно малое![]() .
Поэтому в приближенных вычислениях
часто заменяют
.
Поэтому в приближенных вычислениях
часто заменяют![]() на
на![]() ,
так как
,
так как![]() вычислять проще. При этом получается
следующая формула для приближенного
вычисления значений функции:
вычислять проще. При этом получается
следующая формула для приближенного
вычисления значений функции:
![]() .
.
Из механического и геометрического смысла производной вытекает механический и геометрический смысл дифференциала.
Механический смысл дифференциала:дифференциал – это путь, пройденный
телом за время![]() ,
если его скорость постоянна и равна
,
если его скорость постоянна и равна![]() .
.
Геометрический смысл дифференциала выясним с помощью рисунка.

касательной, соответствующее приращению
![]() аргумента.
аргумента.
Заметим, что
![]() есть приращение ординаты самой кривой,
соответствующее приращению
есть приращение ординаты самой кривой,
соответствующее приращению![]() аргумента.
аргумента.
Дифференциалы конкретных функций
вычисляются по формуле (4.2) с помощью
таблицы производных. Например,
![]() и т.д. Аналогично выводятся правила
вычисления дифференциалов. Например,
и т.д. Аналогично выводятся правила
вычисления дифференциалов. Например,![]()
![]() ,
,![]()
![]() .
Для сложной функции
.
Для сложной функции![]() имеем
имеем![]() .
С другой стороны,
.
С другой стороны,![]() ,
поэтому
,
поэтому![]() .
Таким образом,
.
Таким образом,![]() и тогда, когдах – независимая
переменная (см. (4.2)), и тогда, когда
и тогда, когдах – независимая
переменная (см. (4.2)), и тогда, когда![]() –
функция.
–
функция.
Определение 2. Свойство сохранения
формулы![]() при замене независимой переменнойх
функцией называетсяинвариантностью
формы дифференциала.
при замене независимой переменнойх
функцией называетсяинвариантностью
формы дифференциала.
Это свойство позволяет легко находить
дифференциалы сложных функций. Например,
![]() .
.
§ 5. Производные и дифференциалы высших порядков
Поскольку производная
![]() функции
функции![]() в свою очередь есть функция отх,
по отношению к ней можно ставить вопрос
о существовании и вычислении производной.
в свою очередь есть функция отх,
по отношению к ней можно ставить вопрос
о существовании и вычислении производной.
Определение 1. Производная от
производной функции![]() называетсяпроизводной 2-го
порядка иливторой производной
функции
называетсяпроизводной 2-го
порядка иливторой производной
функции![]() .
Производная от 2-ой производной называетсяпроизводной третьего порядкаилитретьей производнойи т.д.,
производная от производнойn-го
порядка называетсяпроизводной
.
Производная от 2-ой производной называетсяпроизводной третьего порядкаилитретьей производнойи т.д.,
производная от производнойn-го
порядка называетсяпроизводной
![]() -
го порядка. Производные, начиная
со второй, называютсяпроизводными
высших порядкови обозначаются:
-
го порядка. Производные, начиная
со второй, называютсяпроизводными
высших порядкови обозначаются:
![]() или
или![]()
![]()
![]()
![]()
![]() .
.
Могут встречаться и другие обозначения производных высших порядков.
Производная
![]() называется также производной 1-го
порядка.
называется также производной 1-го
порядка.
Примеры производных порядка n:![]()
![]() .
.
Выясним механический смысл 2-ой
производной.
![]() ,
как известно, есть скорость изменения
функции
,
как известно, есть скорость изменения
функции![]() относительно аргументах. Поэтому
2-я производная
относительно аргументах. Поэтому
2-я производная![]() ,
как производная от производной, есть
скорость изменения скорости, т.е.
ускорение изменения функции
,
как производная от производной, есть
скорость изменения скорости, т.е.
ускорение изменения функции![]() относительно аргументах.
относительно аргументах.
Вычислим производную 2-го порядка
функции, заданной параметрически
уравнениями
![]()
![]() .
Заметим, что
.
Заметим, что![]() .
Поступая так же, как при вычислении
первой производной, получим
.
Поступая так же, как при вычислении
первой производной, получим
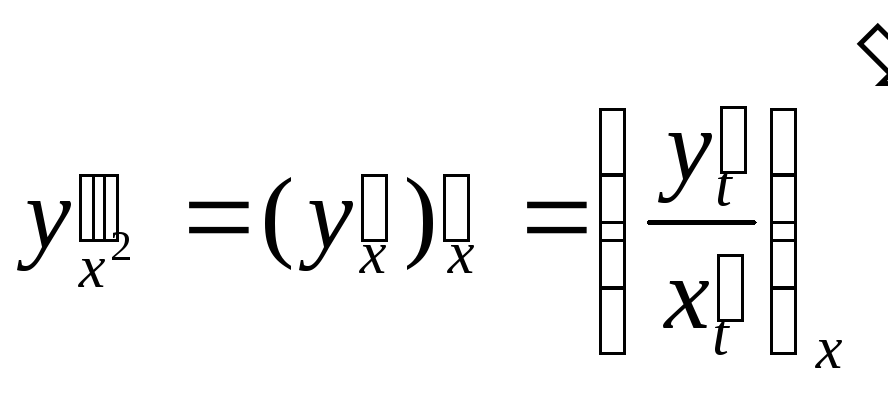
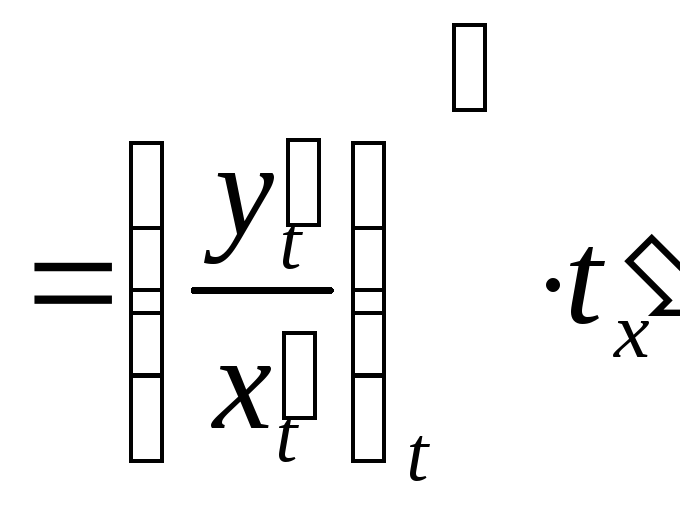 =
=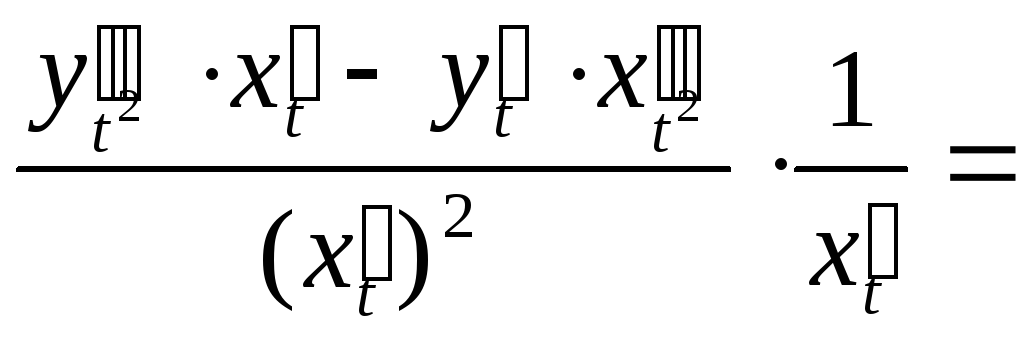
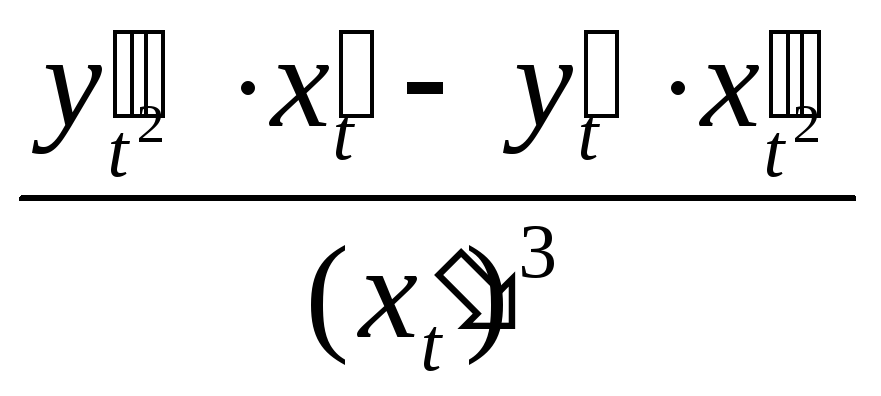 .
.
Таким образом,
![]()
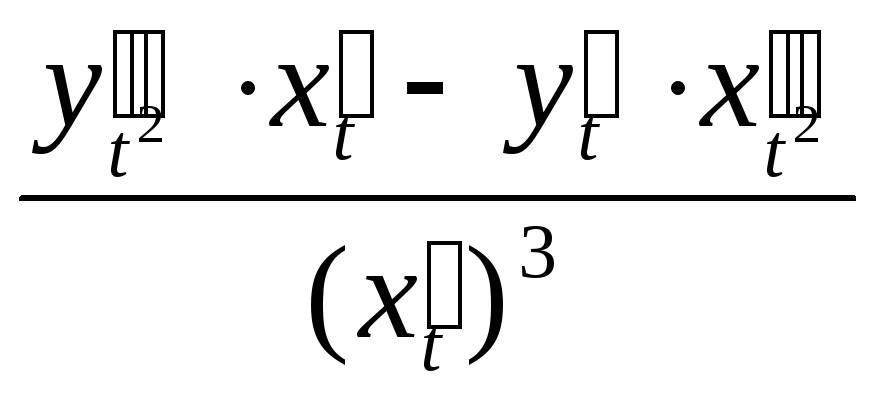 .
.
Определим дифференциалы высших порядков.
Заметим, что в формуле
![]() ,
т.е. отх не зависит,
,
т.е. отх не зависит,![]() − функция отх, значит, и
− функция отх, значит, и![]() есть функция отх. Поэтому можно
говорить о дифференциале от дифференциала
есть функция отх. Поэтому можно
говорить о дифференциале от дифференциала![]() .
.
Определение 2. Дифференциал от
дифференциала функции![]() в некоторой точке называетсядифференциалом
2-го порядка в этой точке
и обозначается
в некоторой точке называетсядифференциалом
2-го порядка в этой точке
и обозначается![]() .
Дифференциал от дифференциала 2-го
порядка называетсядифференциалом
3-го порядка и обозначается
.
Дифференциал от дифференциала 2-го
порядка называетсядифференциалом
3-го порядка и обозначается![]() и т.д. Дифференциал от дифференциала
(n-1)-го порядка называетсядифференциалом n-го
порядка и обозначается
и т.д. Дифференциал от дифференциала
(n-1)-го порядка называетсядифференциалом n-го
порядка и обозначается![]() .
.
Получим формулы для вычисления
дифференциалов высших порядков функции
![]() ,
имеющей в точкех производные
любого порядка. Имеем
,
имеющей в точкех производные
любого порядка. Имеем
![]() ,
,
![]() ,
,
![]()
![]() .
.
Из последней формулы получаем, что
![]() ,
т.е. обозначение
,
т.е. обозначение![]() можно рассматривать не только как
символ, но и как дробь.
можно рассматривать не только как
символ, но и как дробь.
Сохраняется ли инвариантность формы дифференциалов высших порядков? Рассмотрим дифференциал 2-го порядка. Если х – функция, то
![]() .
.
Если же х независимая переменная, то
![]() .
.
Видим, что две последние формулы
отличаются друг от друга слагаемым
![]() ,
т.е. уже для дифференциала 2-го порядка
форма его изменяется при замене
независимой переменной функцией.
,
т.е. уже для дифференциала 2-го порядка
форма его изменяется при замене
независимой переменной функцией.
Таким образом, дифференциалы высших порядков свойством инвариантности формы не обладают.
