§ 2. Дифференцируемые функции. Непрерывность дифференцируемой функции. Производная сложной функции

Определение 1. Функцияназываетсядифференцируемой в точке, если ее приращение в этой точке представимо в виде

, (2.1)

где и не зависит от, апри.

Теорема 1. Функция, дифференцируема в точкетогда и только тогда, когда она имеет в этой точке конечную производную.

Доказательство.Необходимость. Пусть функциядифференцируема в точке, т.е. имеет место равенство (2.1). Разделив его на, получим. Переходя к пределу при, видим, что, т.е. предел правой части существует и равенА, значит, существует и предел левой части, т.е., причем.

Достаточность. Пусть существует. Тогда по теореме 1 § 16 главы 1, где– бесконечно малая функция при. Отсюда, т.е. функция дифференцируема в точке.

Теорема доказана.

Замечание. Из теоремы 1 следует, что понятия функции, имеющей конечную производную, и дифференцируемой функции равносильны. Поэтому дифференцируемой можно назвать функцию, имеющую конечную производную, что и делают авторы некоторых учебников.

Как связаны между собой свойства непрерывности и дифференцируемости функций? Имеет место

Теорема 2. Если функциядифференцируема в точке, то она в этой точке непрерывна.

Доказательство. Поскольку в точке, имеем, что и означает непрерывность функции в точке.

Теорема доказана.

Обратное неверно, то есть существуют непрерывные функции, которые не дифференцируемы.

Пример 1. Покажем, что функциянепрерывна, но не дифференцируема в точке.

Решение. Найдем приращение функции в точке, соответствующее приращениюаргумента. Имеем. Поэтому, то есть функциянепрерывна в точке. С другой стороны,,, то есть односторонние производные в точкене равны, следовательно, данная функция в этой точке не дифференцируема.

В математическом анализе имеются примеры функций, которые в каждой точке числовой прямой непрерывны, но не дифференцируемы. Они имеют сложную конструкцию.

Теорема 3. Пусть функцияимеет в точкепроизводную, функцияимеет в соответствующей точкепроизводную. Тогда сложная функцияимеет в точкепроизводную

или, короче,.

Доказательство. Дадим значениюприращение. Тогда получим соответствующее приращениефункциии приращениефункции. В силу теоремы 1 имеем

, гдепри.

Отсюда

.

Заметим, что если , то ипо теореме 2, поэтому и. Следовательно,.

Поскольку существует предел правой части равенства, то существует и предел левой части и

.

Теорема доказана.

Замечание. Теорема 3 доказана для случая, когда сложная функцияимеет одну промежуточную переменную. Если промежуточных переменных несколько, то производная вычисляется аналогично. Например, если,,, то.

§ 3. Правила дифференцирования. Производные основных элементарных функций

Теорема 1. Пусть функция, непрерывна, строго монотонна на отрезкеи дифференцируема во внутренней точкеэтого отрезка, причем. Тогда обратная функциядифференцируема в точке, причем.

Доказательство. Заметим, что в условиях теоремы обратная функциясуществует, непрерывна и строго монотонна на отрезкев силу теоремы из § 19 главы 1.

Придадим значению приращение. Тогдаполучит приращение

(так как функциястрого монотонна). Поэтому можно записать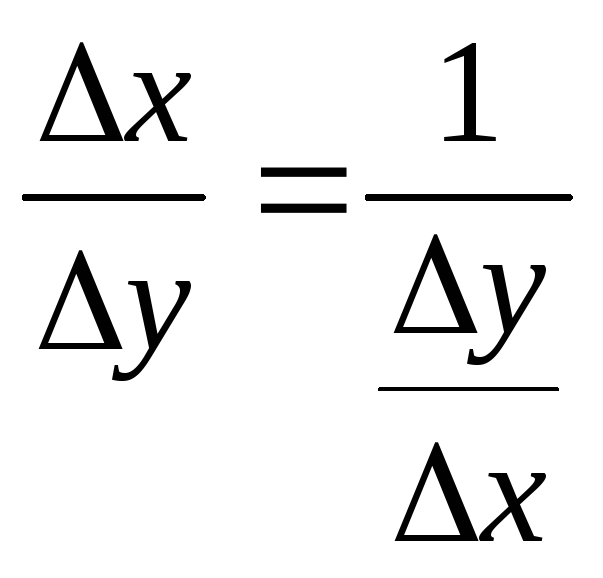. Поскольку прив силу непрерывности обратной функции ии, по условию, существует, имеем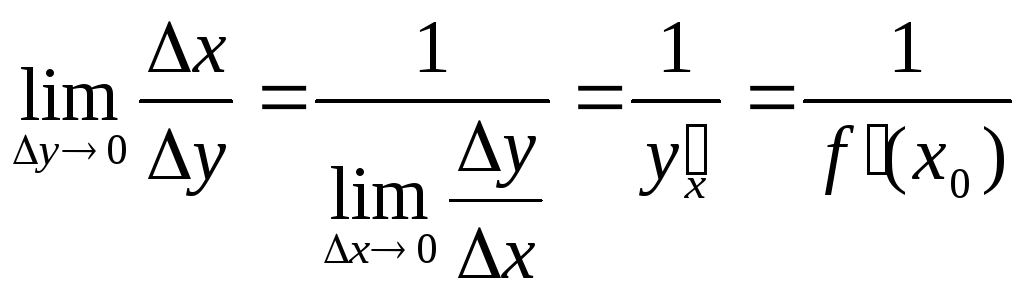. Отсюда следует существованиеи равенство. Теорема доказана.

Пример 1. Найдем производные функцийarcsin x,arccos x,arctg x,arcctg x/

Решение. По теореме 1 имеем(поскольку, имееми корень берем со знаком плюс).

Аналогично,

,

,.

Теорема 2. Если функциииимеют производные в точке, то в точкеимеют производные и функции(если) и справедливы формулы

а);б);в).

Доказательство.а) Пусть. Дадимприращение. Тогда функцииu,v,yполучат приращения, причем

. Отсюдаии равенствоа) доказано.

б) Пусть. Аналогично пунктуа) имеем

,,, т.е. имеет место формулаб).

в) Пусть. Имеем,,, т.е. имеет место формулав).

Теорема доказана.

Следствия. 1) Если, то.

2) Формула а) имеет место для любого конечного числа слагаемых.

3) .

Доказательство. 1) Поскольку, имеем.

2) Например, имеем .

3) Например, имеем .

В общем случае следствия 2) и 3) доказываются методом математической индукции.

Рассмотрим показательно-степенную функцию , гдеu иv– некоторые функции отх. Найдем производную функцииу в точке, в которой дифференцируемы функцииu иv.Для этого представим функциюув виде.По правилу дифференцирования сложной функции, в силу теоремы 2 и примера 1 § 1 имеем

.

Таким образом,

.

Заметим, что в полученной формуле первое слагаемое есть результат дифференцирования как показательной функции, а второе – как степенной функции. Примененный прием дифференцирования называетсялогарифмическим дифференцированием. Им бывает удобно пользоваться и тогда, когда дифференцируемая функция является произведением нескольких сомножителей.

Перейдем теперь к параметрическому заданию функций. Если зависимость функции у от аргументах устанавливается не непосредственно, а с помощью некоторой третьей переменнойt, называемой параметром, формулами

, (3.1)

то говорят, что функция у отх задана параметрически.

Если х и у рассматривать как прямоугольные координаты точки на плоскости, то уравнения (3.1) ставят в соответствие каждому значениюточкуна плоскости. С изменениемtточкаопишет некоторую кривую на плоскости. Уравнения (3.1) называются параметрическими уравнениями этой кривой. Например, уравнения

(3.2)

являются параметрическими уравнениями эллипса с полуосями а иb.

Если в (3.1) уравнение разрешается относительноt,, то параметрическое задание функции можно свести к явному:

.

Найдем производную функции, заданной параметрически. Для этого предположим, что функцииидифференцируемы, причемна некотором промежутке, а для функциисуществует обратная функция, имеющая конечную производную. Тогда по правилу дифференцирования сложной и обратной функций находим:. Таким образом,

. (3.3)

Например, производная функции, определяемой уравнениями (3.2) имеет вид

.

Уравнение касательной к кривой, заданной параметрически, в точке , соответствующей значению параметра, получается из уравнения (1.4), если вместоподставить:

,

отсюда при имеем

. (3.4)

Аналогично из уравнения (1.5) получаем уравнение нормали:

или. (3.5)

Запишем теперь сводные таблицы производных основных элементарных функций и правил дифференцирования, полученных ранее.

Правила дифференцирования

1. . 2.. 3.. 4..

5. Если , то. 6. Еслито.

7. Если– обратная функция, то. 8..

Таблица производных основных элементарных функций

1. , где. 2., в частности,

3. . 4...

5. . 6..

7. . 8..

9. . 10..

11. , в частности,. 12., в частности,.