§ 14. Показательная функция

Определение 1. Функция виданазываетсяпоказательной функцией.

Согласно §13 . Поскольку приа = 1 имеем, т.е. функция постоянная, будем предполагать в дальнейшем, что.

Теорема 1. Если, то функциястрого возрастает, если, тострого убывает.

Доказательство. Пусть– произвольные действительные числа,,– рациональные числа. Пусть. В силу усиленной плотности множестваRнайдем рациональные числа. Начиная с некоторого(лемма 2) и, аналогично, поэтому, т.е.строго возрастает.

Если , то, поэтому, т.е.строго убывает. Теорема доказана.

Следствие. Показательная функция не имеет точек экстремума.

Теорема 2. Функция,, всюду непрерывна.

Доказательство. Пусть– произвольная точка,– произвольная

последовательность точек. Между числами и,ивозьмем рациональные числаи,n= 1, 2, … соответственно (это можно сделать в силу усиленной плотности множестваR). Тогдаи. Поэтому по формуле (13.4). Поскольку по теореме 1 при, а при, то по теореме о промежуточной переменной. В силу произвольности последовательности, сходящейся к, функциянепрерывна в точкепо Гейне. Теорема доказана.

Следствие. Криваявертикальных асимптот не имеет.

Теорема 3. Если, то

1) ; 2); 3).

Доказательство. Поскольку, можно записать, где. Тогда по неравенству Бернулли. Какое быни взять, найдетсятакое, что привыполняется неравенство(достаточно взять). Поскольку– возрастающая функция, то приимеем, а это и означает, что, то есть 1) доказано.

Докажем 2). Имеем .

3) следует из 2) и строгого возрастания функции при. Теорема доказана.

Следствия. 1) Если, то,,.

Для доказательства достаточно рассмотреть . Тогда,.

2) Из 2) следует, что – горизонтальная асимптота придляи придля. Наклонных асимптот нет, так какпри,прии. Аналогичные рассуждения проводятся и для.

3) область значений показательной функции – множество Это следует из теорем 3, 2 и 2-ой теоремы Больцано-Коши.

Поскольку , то кривая выпукла вниз на, точек перегиба нет.

График функции имеет вид:

у,

,

1

О х

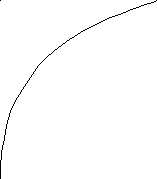
§ 15. Логарифмическая функция

Определение 1. Функция, обратная к показательной функции, называетсялогарифмической функциейи обозначается.

Заметим, что данное определение корректно, т.е. логарифмическая функция существует в силу строгой монотонности показательной функции припо теореме о существовании и непрерывности обратной функции.

Если и, то логарифмы называют десятичными и натуральными и обозначаютисоответственно.

Из свойств взаимно-обратных функций следует, что . Логарифмическая функция не является ни четной, ни нечетной. Непериодическая. По теореме о существовании и непрерывности обратной функции она непрерывна в области определения, то есть точек разрыва не имеет, пристрого возрастает отдо, пристрого убывает отдо, поэтому точек экстремума не имеет.поэтому– вертикальная асимптота.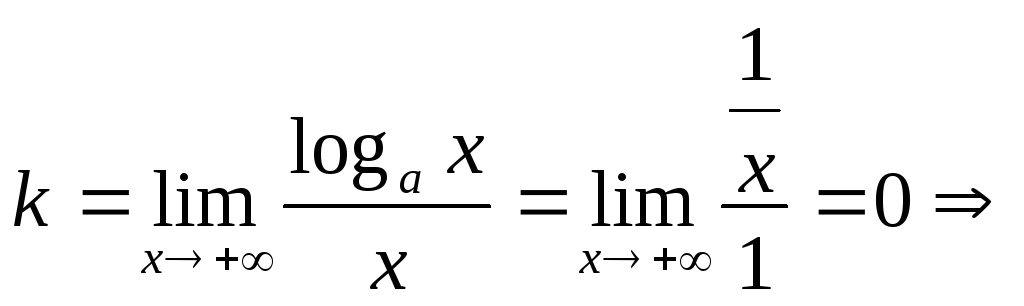наклонных асимптот нет.горизонтальных асимптот нет., так как, то есть точка (1; 0) – точка пересечения графика с осью, с осьюОу пересечения нет, так как.наина (0; 1) при, а прина (0; 1) ина.точек перегиба нет. Если, тои кривая выпукла вверх в, если, тои кривая выпукла вниз в.

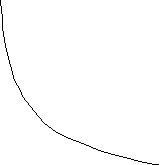
Заметим, что в силу свойства графиков взаимно-обратных функций кривыеисимметричны относительно прямой.

у

О 1х

Справедливы следующие свойства логарифмов, известные из школьного курса математики:

1. .

2. .

3. , где, а также формула перехода от одного основания логарифма к другому

.