
- •§ 8. Условия постоянства, возрастания и убывания функции
- •§ 9. Экстремум функции. Наибольшее и наименьшее значения функции на отрезке
- •§ 10. Выпуклые кривые. Точки перегиба кривой
- •§ 11. Асимптоты кривой
- •§ 12. Полное исследование функций и построение их графиков
- •§ 13. Определение и свойства степени
- •§ 14. Показательная функция
- •§ 15. Логарифмическая функция
- •§16. Степенная функция
- •§ 17. Тригонометрические функции
§ 11. Асимптоты кривой
Понятие асимптоты кривой вводится для кривых, ветви которых уходят в бесконечность. Это может быть в случаях, когда функция не ограничена или когда она задана на неограниченном промежутке.
Определение. Прямая линия называетсяасимптотой кривой![]() ,
если расстояние от точкиМ, лежащей
на кривой, до этой прямой стремится к
нулю при движении точкиМ вдоль
какой-нибудь части кривой в бесконечность.
,
если расстояние от точкиМ, лежащей
на кривой, до этой прямой стремится к
нулю при движении точкиМ вдоль
какой-нибудь части кривой в бесконечность.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты.
у
Уравнение вертикальной асимптоты имеет
вид
![]() .
РасстояниеМАот точки
.
РасстояниеМАот точки![]() до
прямой
до
прямой![]() равно
равно![]() .
.![]() тогда, когда
тогда, когда![]() или
или![]() .
Чтобы прямая
.
Чтобы прямая![]() была асимптотой кривой
была асимптотой кривой![]() ,
нужно, по определению, чтобы при
,
нужно, по определению, чтобы при![]() или при
или при![]() функция
функция![]() стремилась к
стремилась к![]() или
или![]() .
.


![]()
 А М
А М
 х
х
О
![]()
![]()
Таким образом, чтобы найти вертикальные асимптоты, нужно исследовать поведение функции вблизи точек разрыва и границ области определения.
Пример 1. Найдем вертикальные
асимптоты кривой![]() .
.
Решение. Функция![]() определена и непрерывна всюду, кроме
точки
определена и непрерывна всюду, кроме
точки![]() .
Исследуем поведение функции при
.
Исследуем поведение функции при![]() и
и![]() :
:![]() ,
,![]() .
Отсюда следует, что прямая
.
Отсюда следует, что прямая![]() (осьОу) – вертикальная асимптота.
Кривая приближается к ней и слева, и
справа.
(осьОу) – вертикальная асимптота.
Кривая приближается к ней и слева, и
справа.
Горизонтальные асимптоты.
Уравнение горизонтальной асимптоты
имеет вид



![]() .
РасстояниеМВот точки
.
РасстояниеМВот точки![]() до
прямой
до
прямой![]() равно
равно![]() .
Чтобы это расстояние стремилось к нулю
при
.
Чтобы это расстояние стремилось к нулю
при![]() или
или![]() ,
нужно, чтобы
,
нужно, чтобы![]() или
или![]() .
.
 В у =А
В у =А
![]()
М
О х
Таким образом, горизонтальные асимптоты могут быть только у кривых, заданных на неограниченном промежутке. Для их отыскания нужно найти пределы функции на бесконечности.
Пример 2. Найдем горизонтальные
асимптоты кривой![]() .
Построим эту кривую.
.
Построим эту кривую.
Решение. Имеем![]() ,
поэтому прямая
,
поэтому прямая![]() (осьОх) является горизонтальной
асимптотой кривой
(осьОх) является горизонтальной
асимптотой кривой![]() и при
и при![]() ,
и при
,
и при![]() .
.
Т ак
как
ак
как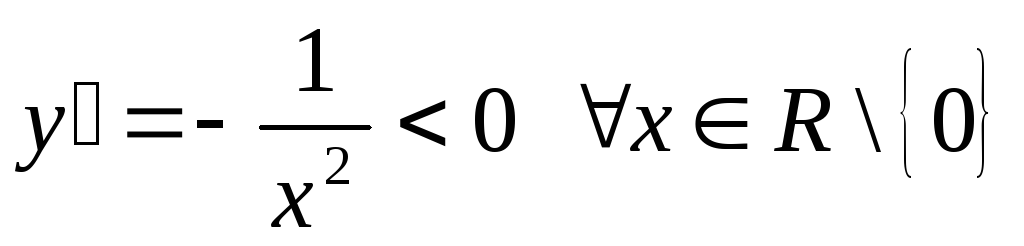 ,
то функция
,
то функция ![]() убывает на интервалах
убывает на интервалах![]() и
и![]() .
Поскольку
.
Поскольку![]() ,
то
,
то![]() при
при![]() и
и![]() при
при![]() ,
откуда следует, что
,
откуда следует, что![]() –
интервал выпуклости вверх кривой, а
–
интервал выпуклости вверх кривой, а![]() –
интервал выпуклости вниз. Учитывая, что
–
интервал выпуклости вниз. Учитывая, что![]() –
вертикальная асимптота (см. пример 1),
строим график.
–
вертикальная асимптота (см. пример 1),
строим график.
 у
у
![]()

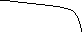 О х
О х
Н




аклонные асимптоты.
Наклонная асимптота имеет уравнение
![]() ,
где
,
где![]() .
Чтобы найти постоянныеk
иb, вычислим
расстояние от точки
.
Чтобы найти постоянныеk
иb, вычислим
расстояние от точки![]() до
прямой
до
прямой![]() .
Это расстояние равноMN,
где отрезокMN
перпендикулярен прямой. ПустьМК– перпендикуляр к осиОх. Тогда
.
Это расстояние равноMN,
где отрезокMN
перпендикулярен прямой. ПустьМК– перпендикуляр к осиОх. Тогда![]() ,
,![]()
![]()
К
N M
О
![]() х
х
![]() ,
где
,
где![]() .
Угол
.
Угол![]() ,
поэтому
,
поэтому![]()
![]() при
при![]() или
или![]() .
Таким образом, условие
.
Таким образом, условие
![]() (*)
(*)
является необходимым и достаточным для
того, чтобы прямая
![]() была асимптотой кривой
была асимптотой кривой![]() .
Найдем постоянныеk
иb. Из условия (*)
следует, что
.
Найдем постоянныеk
иb. Из условия (*)
следует, что
![]() или
или![]() ,
,
откуда
![]() .
(11.1)
.
(11.1)
Из условия (*) следует также, что
![]() .
.
Таким образом, чтобы найти уравнение наклонной асимптоты, нужно найти коэффициент k по формуле (11.1), подставить его в формулу
![]() (11.2)
(11.2)
и найти коэффициент b.
Если пределы в (11.1) и (11.2) существуют и
конечны, причем![]() ,
то существует и наклонная асимптота,
ее уравнение
,
то существует и наклонная асимптота,
ее уравнение![]() .
.
Пример 3. Найдем наклонные асимптоты
кривой![]() .
.
Решение. Имеем![]() ,
то есть
,
то есть![]() и при
и при![]() ,
и при
,
и при![]() ;
;![]() .
Таким образом,
.
Таким образом,![]() –
наклонная асимптота данной кривой и
при
–
наклонная асимптота данной кривой и
при![]() ,
и при
,
и при![]() .
.
