§ 8. Условия постоянства, возрастания и убывания функции

Теорема 1 (условие постоянства функции). Пусть функцияопределена и непрерывна на промежуткеХ и имеет внутри него конечную производную. Для того чтобыбыла постоянной наХ, необходимо и достаточно условиевнутриХ.

Доказательство.Необходимость.

Пусть на промежуткеХ. Тогда внутриХ , то есть условие теоремы выполнено.

Достаточность.

Зафиксируем точку и возьмем произвольную точку. К отрезку применим формулу Лагранжа (6.2) (это можно сделать, так как на этом отрезке функциянепрерывна и внутри него имеет конечную производную по условию теоремы), получим, так каквнутриХ, а. Отсюда следует, что, т.е. постоянна наХ. Теорема доказана.

Теорема 2 (условие монотонности функции). Пусть функцияопределена и непрерывна на промежуткеХ и имеет внутри него конечную производную. Для того чтобыбыла наХнеубывающей (невозрастающей), необходимо и достаточно условиевнутриХ.

Доказательство. Рассмотрим случай неубывающей функции.

Необходимость. Пусть функцияне убывает наХ. Возьмем внутри промежуткаХ произвольную точкухи. Тогдаи, переходя в последнем неравенстве к пределу при, получим.

Достаточность. ПустьвнутриХ. Возьмем произвольные точки,и применим формулу Лагранжа (6.2) на отрезке:, так как. Поэтому, то есть функцияявляется неубывающей.

Аналогично рассматривается случай невозрастающей функции. Теорема доказана.

Теорема 3 (достаточное условие строгой монотонности функции). Если функцияопределена и непрерывна на промежуткеХ, внутри него имеет конечную производнуюи всюду внутриХ , тострого возрастает (убывает) наХ.

Доказательство. Возьмем произвольные точки,и применим кна отрезкеформулу Лагранжа (6.2):, где. Поскольку, из условияследует, что, то естьстрого возрастает, а из условияследует, что, то естьстрого убывает. Теорема доказана.

Замечание. Условиене является необходимым для строгого возрастания (убывания) функции. Например, для функциив точке, в то же время эта функция строго возрастает на всей числовой прямой. Вообще, еслиобращается в нуль в конечном числе точек, а в остальных точках сохраняет знак, то– строго монотонная функция. Для доказательства этого достаточно применить формулу Лагранжа к промежуткам между соседними нулями производной.

Определение 1. Функцияназываетсявозрастающей (убывающей)в точке , если существует окрестностьточки такая, что функция определена в этой окрестности и знак приращения функциив этой окрестности совпадает со знаком (противоположен знаку) приращения аргумента.

у

Если , то

для ,

для ,

поэтому функция возрастает

в точке .

Ох

◦ ◦

Теорема 4 (достаточное условие монотонности функции в точке). Если функцияопределена в некоторой окрестности точкии имеет в этой точке положительную производную, то функциявозрастает в точке. Если же, тоубывает в точке.

Доказательство. В силу теоремы 1 § 2

, гдепри. Посколькупри, а, существуеттакое, чтоприили. Если, то в окрестности, откудаи знаксовпадает со знаком, т.е. функциявозрастает в точке. Если, то, откудаи знакпротивоположен знаку, т.е. функцияубывает в точке. Теорема доказана.

Пример. Найдем интервалы монотонности функции.

Решение. Найдем область определения функции: функция существует, когдаи, то есть. Далее,=, в области определениясуществует. Отметим на числовой прямой область определения функции и точку, в которой производная равна нулю. После этого определим в каждом из полученных промежутков знак производной с помощью пробных точек:,.

– – +

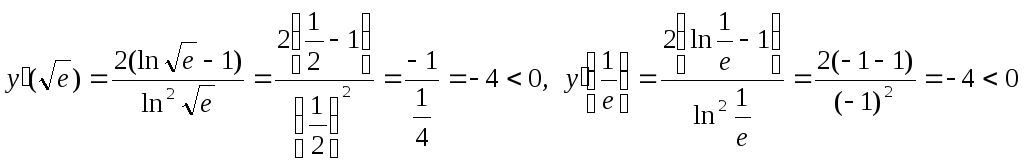0 1 е

Видим, что функция убывает на интервалах (0; 1) и (1; е), возрастает на интервале.