
Часть II Вариант 15.
-
Построить на плоскости область допустимых решений системы линейных неравенств:

Точки граничных прямых:
|
|
|
|
|
|||
|
|
0 |
-6 |
0 |
2 |
0 |
6 |
|
|
4 |
0 |
1 |
0 |
12 |
0 |

2.
Решить
задачу линейного программирования
симплекс-методом. Ответ проверить
графически
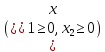 .
.

 .
.
1) Задача минимизации
Перейдем
от системы неравенств к системе уравнений
путем добавления базисных неизвестных :
:


Составим симплекс матрицу:
|
|
|
|
|
|
|
|
-3 |
2 |
1 |
0 |
0 |
12 |
|
-4 |
1 |
0 |
1 |
0 |
4 |
|
7 |
-3 |
0 |
0 |
1 |
21 |
|
1 |
-2 |
0 |
0 |
0 |
0 |
В данной матрице не выполняются ни критерий оптимальности, ни критерий отсутствия оптимальности, поэтому необходимо выбрать разрешающий элемент и перейти к следующей матрице.
Разрешающий столбец - 1-ый, разрешающий элемент – 3-ий
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
|
147/7 |
( |
|
0 |
|
0 |
1 |
|
112/7 |
( |
|
1 |
-3/7 |
0 |
|
1/7 |
3 |
( |
|
0 |
-11/7 |
0 |
0 |
-1/7 |
-3 |
|
Т.к. в целевой строке все элементы неположительные, то выполняется критерий оптимальности, т.е. задача имеет оптимальное решение, равное:
 ;
;
 (3,0,
147/7,
112/7,0);
(3,0,
147/7,
112/7,0);
Контроль:
 .
.
2) Задача максимизации

Составим симплекс матрицу:
|
|
|
|
|
|
|
|
-3 |
2 |
1 |
0 |
0 |
12 |
|
-4 |
1 |
0 |
1 |
0 |
4 |
|
7 |
-3 |
0 |
0 |
1 |
21 |
|
-1 |
2 |
0 |
0 |
0 |
0 |
Разрешающий столбец - 2-ой, разрешающий элемент – 2-ой.
|
|
|
|
|
|
|
|
5 |
0 |
1 |
-2 |
0 |
4 |
|
-4 |
1 |
0 |
1 |
0 |
4 |
|
-5 |
0 |
0 |
3 |
1 |
33 |
|
7 |
0 |
0 |
-2 |
0 |
-8 |
Разрешающий столбец - 4-ый, разрешающий элемент – 3-ий.
|
|
|
|
|
|
|
|
1 |
0 |
1/5 |
-2/5 |
0 |
4/5 |
|
0 |
1 |
4/5 |
-3/5 |
0 |
36/5 |
|
0 |
0 |
1 |
1 |
1 |
185/5 |
|
0 |
0 |
-7/5 |
4/5 |
0 |
-68/5 |
Разрешающий столбец - 1-ый, разрешающий элемент – 1-ый.
|
|
|
|
|
|
|
|
|
1 |
0 |
|
0 |
|
78/5 |
( |
|
0 |
1 |
|
0 |
|
147/5 |
( |
|
0 |
0 |
1 |
1 |
1 |
185/5 |
( |
|
0 |
0 |
-11/5 |
0 |
-4/5 |
-216/5 |
|


Контроль:

3) Проверка ответа графически:
|
|
|
|
|
|||
|
|
0 |
-4 |
0 |
-1 |
0 |
3 |
|
|
6 |
0 |
4 |
0 |
-7 |
0 |

ABOCD - область допустимых решений.
Вектор
 .
.
т. A - точка максимума с координатами:

т.
C
- точка минимума с координатами: D(3,
0)
D(3,
0)
3.
Составить
двойственную задачу к данной, решить
одну их них симплекс - методом и найти
решение другой
 :
:

 .
.
Составим задачу, двойственную к исходной:


Решим симплекс-методом двойственную задачу:
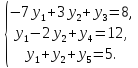

где,
 - базисные неизвестные.
- базисные неизвестные.
|
|
|
|
|
|
|
|
-7 |
3 |
1 |
0 |
0 |
8 |
|
1 |
-2 |
0 |
1 |
0 |
12 |
|
1 |
1 |
0 |
0 |
1 |
5 |
|
3 |
-1 |
0 |
0 |
0 |
0 |
Разрешающий столбец – 1-ый, разрешающий элемент – 3-ий.
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
|
43 (=8+35) |
( |
|
0 |
|
0 |
1 |
|
7 (=12-5) |
( |
|
1 |
1 |
0 |
0 |
1 |
5 |
( |
|
0 |
-4 |
0 |
0 |
-3 |
-15 (=-5·3) |
|
|
|
|
|
|
|
|
|
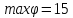

Контроль:

Решение основной задачи:
т.к. ,
то
,
то


Контроль:



 (2)
(2) (3)
(3)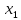
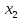
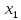














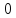







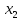
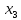














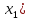





 (2)
(2) (3)
(3)

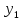










 )
)

 )
) )
)

