Цепи с распределёнными параметрами

•Чтобы учесть изменение тока и напряжения вдоль передающей линии, необходимо рассматривать каждый сколь угодно малый элемент, как обладающий сопротивлением и индуктивностью, а при параллельном расположении проводов – проводимостью и емкостью линии, т.е. рассматривать линию, как цепь с распределенными параметрами или длинную линию.

•Линию называют однородной, если сопротивление, индуктивность, проводимость и емкость равномерно распределены вдоль линии.

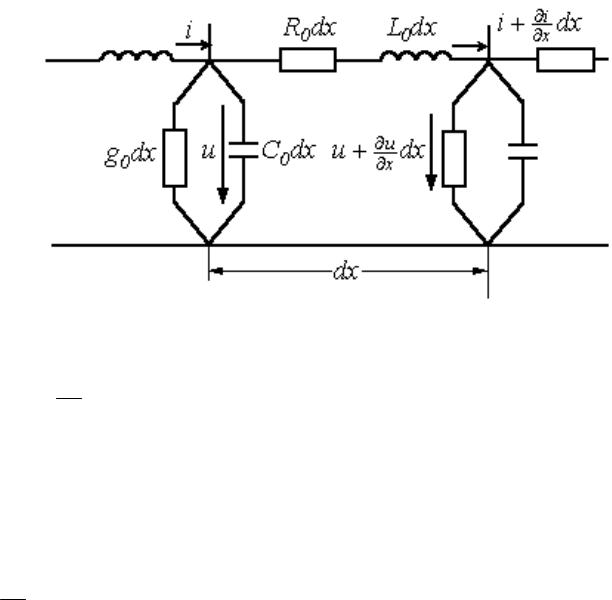
• u, i – напряжение и ток в начале участка;

• u u , i i - напряжение и ток в конце участка;

x x

•R0 – продольное активное сопротивление единицы длины линии;

•L0 – индуктивность длины линии;

•C0- емкость единицы длины линии;

•G0 – поперечная проводимость единицы длины линии.

•Gu0 неiв коем случае не является величиной, обратной R0.

•x , x - скорость изменения напряжения и тока вдоль оси х.

•Рассмотрим установившийся режим в длинной линии, для чего запишем (1) и (2) в комплексном виде:

сопротивление и проводимость на единицу длины линии.

• где A1, A2 - комплексные постоянные интегрирования; α – коэффициент затухания;

•Характеристическое сопротивление характеризует степень согласования линии, т.е. степень передачи мощности генератора нагрузке, если рассматривать линию как четырехполюсник.

•На основании (4), (5) и (6) значения напряжения и тока примут вид:

u 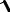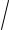2 A1e x sin( t x 1 ) 2 A2e x sin( t x 2 )

перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны.

•Будем считать, что положительное направление тока прямой волны совпадает с положительным направлением тока , а положительное направление обратной волны – противоположно направлению тока. Тогда, вводя обозначения

т.е. токи прямой и обратной волны связаны между собой законом Ома.

•Если заданы токи и напряжения в конце линии, то аналогично получаем: