Министерство образования и науки РФ

Федеральное агентство по образованию

Саратовский государственный технический университет

Изучение однофазной цепи

ПЕРЕМЕННОГО ТОКА

С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ

АКТИВНОГО СОПРОТИВЛЕНИЯ,

ИНДУКТИВНОЙ КАТУШКИ

И КОНДЕНСАТОРА

Методические указания к лабораторной работе

по курсу “Электротехника и основы электроники”

для студентов неэлектрических специальностей

Электронное издание локального распространения

Одобрено

редакционно-издательским советом

Саратовского государственного

технического университета

Саратов 2006

Все права на размножение и распространение в любой форме остаются за разработчиком.

Нелегальное копирование и использование данного продукта запрещено.

Составители: Беляева Юлия Александровна

Под редакцией Б.К. Сивякова

Рецензент А.А. Гурьянов

410054, Саратов, ул. Политехническая, 77, Научно-техническая библиотека СГТУ

тел.: 52-63-81, 52-56-01

http://lib.sstu.ru

Регистрационный

номер

© Саратовский государственный

технический университет, 2006

Цель работы: экспериментальное изучение линейной цепи синусоидального тока, состоящей из параллельно соединённых активного сопротивления, индуктивной катушки и конденсатора; изучение основных закономерностей в такой цепи, изучение резонанса токов.

Основные понятия

Схема одного из простейших вариантов электрической цепи, содержащей параллельно соединённые активные сопротивления, индуктивную катушку и конденсатор, приведена на рис. 1.

На рис. 1. обозначены:

U – действующее значение синусоидального напряжения, подключенного к цепи;

I, I₁, I₂ - действующие значения синусоидальных токов в неразветвлённой части цепи, в ветви с индуктивным элементом и в ветви с конденсатором соответственно.

Токи I₁ и I₂ в каждой из ветвей могут быть найдены по соотношениям

,

где Z – полное сопротивление ветви, содержащее последовательно соединённые активный и индуктивный элементы;

- реактивное индуктивное сопротивление;

- угловая частота токов и напряжений в цепи.

где – полное сопротивление ветви, содержащей последовательно соединённые активные сопротивления и конденсатор;

- реактивное емкостное сопротивление.

Токи I₁ и I₂ сдвинуты по фазе относительно напряжения U на углы исоответственно. При этом

Ток I в неразветвлённой части цепи может быть определён графоаналитическим методом. Для узлов “а” и “б” цепи выполняется первый закон Кирхгофа в векторной форме:

Векторная диаграмма цепи изображена на рис. 2. На векторной диаграмме цепи (рис.2) - угол сдвига по фазе между напряжениеми током.

Более точен аналитический метод проводимостей. Для применения этого метода каждый из токов раскладывают на две составляющие. Одна из составляющих – проекция на ось, совпадающую по направлению с вектором напряжения /активная составляющая/, другая – проекция на ось, перпендикулярную вектору напряжения/реактивная составляющая/. Соответствующая такому разложению векторная диаграмма также показана на рис.2. Индекс “а” для токов на диаграмме соответствует активной составляющей, индекс “р” – реактивной.

Для составляющих токов справедливы соотношения:

- активная проводимость ветви, содержащей индуктивный элемент;

- реактивная индуктивная проводимость ветви, содержащей индуктивный элемент;

- активная проводимость ветви, содержащей конденсатор;

- реактивная емкостная проводимость ветви, содержащей конденсатор.

; ; ;

где - активная проводимость эквивалентной цепи.

,

где - реактивная проводимость эквивалентной цепи.

,

где - полная проводимость эквивалентной цепи.

,

где - полное сопротивление эквивалентной цепи.

,

где - активное сопротивление эквивалентной цепи.

.

где - реактивное сопротивление эквивалентной цепи.

Углы сдвига по фазе входного напряжения относительно соответствующих токов определяются соотношениями:

Мощности в цепи определяются по соотношениям:

активные мощности

,

где и - активные мощности ветвей;

реактивные мощности

,

где - реактивная индукционная мощность;

где - реактивная емкостная мощность.

.

где - полная мощность.

В цепи, схема которой приведена на рис. 1, возможен резонанс токов. Резонанс токов – это явление, наступающее в цепи синусоидального тока, содержащей параллельно соединённые ветви, отличающиеся между собой типом реактивной проводимости, заключающееся в том, что ток в неразветвлённой части цепи совпадает по фазе с приложенным ко всей цепи напряжением.

При резонансе токов выполняются следующие соотношения:

/ это условие возникновения резонанса в цепи /

; ; ;

,

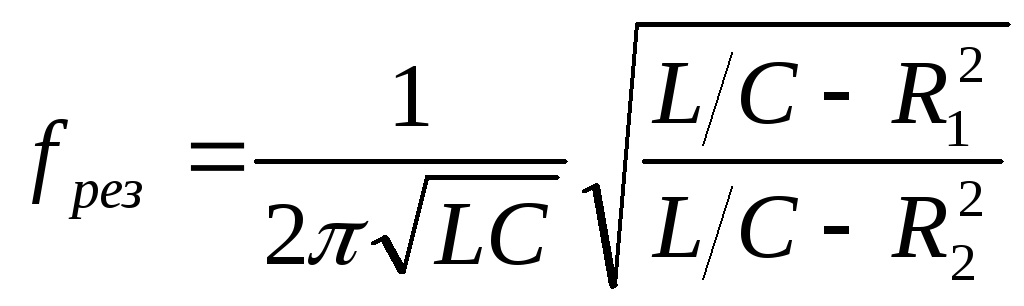где - частота напряжения и токов в цепи, соответствующая резонансу.

Для идеального случая цепи без потерь

и .

Для коэффициента мощности выполняется соотношение

; ;

Все использованные в настоящем разделе величины в Международной системе единиц “СИ” измеряются в следующих единицах:

напряжение - В

токи - А

активная мощность - Вт

реактивная мощность - вар

частота - Гц

угловая частота - рад/с

сопротивление - Ом

проводимость - См = 1/Ом

Рис. 1

Рис. 2