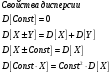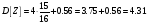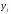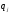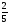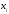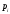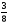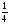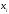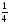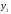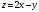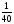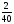Desktop / Primer_vypolnenia_individualnoy_raboty_1

Задание.

Для двух независимых случайных величин х и у с законами распределения, заданными соответствующими таблицами, выполните следующее:

1. заполните пустые места в таблицах;

2. Вычислите основные характеристики (математическое ожидание и дисперсию) для случайных величин

3. постройте закон распределения случайной величины z , являющейся линейной комбинацией случайных величин х и у ;

4. найдите M[z] и D[z] (двумя способами):

а) используя таблицу закона распределения случайной величины z;

б) используя свойства математического ожидания и дисперсии случайной величины.

	2	3	4

	0	1	2	3

_{Решение.}

1. Заполнить пустые места в таблицах, используя основное свойство закона распределения: (сумма вероятностей должна быть равна 1)

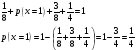
	0	1	2	3

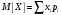
Дисперсия может быть вычислена двумя способами. Так как математическое ожидание получилось дробным, то удобнее использовать вторую формулу.

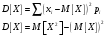
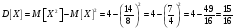
	2	3	4

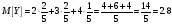
3. Составить закон распределения случайной величины

		0	1	2	3
2		-2	0	2	4
3		-3	-1	1	3
4		-4	-2	0	2

Таблица 1

Заполняем возможные значения случайной величины z в порядке возрастания.

	-4	-3	-2	-1	0	1	2	3	4

Используя таблицу 1 и исходные таблицы, определяем вероятности событий.

принимает значение -4, если (см. таблицу 1).

По исходным таблицам для x и y определяем вероятности наступления этих событий.

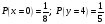
Так как они должны наступить одновременно, то перемножаем эти вероятности.

Аналогично вычисляем вероятности остальных событий.

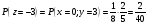
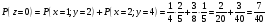
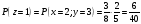
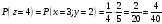
Получили закон распределения.

	-4	-3	-2	-1	0	1	2	3	4

Проверка

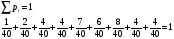
3. Вычислить математическое ожидание по определению

Вычислить математическое ожидание, используя свойства.

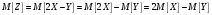
Вычислить математические ожидания исходных случайных величин.

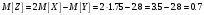
Результаты, вычисленные первым и вторым способами, совпадают.

3. Вычислить дисперсию случайной величины Z

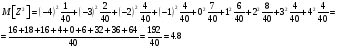
Вычислить дисперсию, используя свойства