
Ч2-34час-ЭлМагн-ВсеСеминары
.docЗадачи для самостоятельной работы
Задача №1 Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол . Шарики погружаются в масло плотностью 0 = 8102 кг/м3. Определить диэлектрическую проницаемость масла, если угол расхождения нитей при погружении шариков в масло остаётся неизменным. Плотность материала шариков = 1.6103 кг/м3
Задача №2 В вершинах квадрата находятся одинаковые заряды Q=0,3 нКл каждый. Какой отрицательный заряд Q1 нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
Задача №3 Положительный точечный заряд 50 мкКл находится на плоскости ХУ в точке с радиус-вектором r0 = 3i + 2j, где i и j — орты осей x и y. Найти модуль и направление вектора напряженности электрического поля E в точке с радиус-вектором r = 9i - 6j. Здесь r0 и r в метрах.
Задача №4 Находящийся в вакууме очень тонкий прямой стержень длины 2a заряжен с одинаковой всюду линейной плотностью λ. Для точек, лежащих на оси стержня, найти модуль E напряженности поля как функцию расстояния от центра стержня, обозначить направление вектора E, найти потенциал ϕ.
Задача №5 По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью λ. Определить напряженность E поля и потенциал ϕ, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина нити составляет половину длины дуги окружности и равна l.
Задача №6 Заряд q=1 нКл распределён по шару радиуса R=10 см с объёмной плотностью, пропорциональной расстоянию r от центра шара. Найти с помощью теоремы Гаусса напряжённость поля E(r), а так же любым известным способом потенциал ϕ(r) внутри шара как функцию r.
Задача №7 В середине грани куба расположен заряд q. Найти поток вектора Е через поверхность куба.
Задача №8 Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями σ1=1 нКл/м2 и σ2=3 нКл/м2. Определить напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам. Найти разность потенциалов между пластинами.
Задача №9 Найти силу взаимодействия двух молекул воды отстоящих друг от друга на расстоянии l=10 нм. Электрический дипольный момент молекулы воды p=0,62·10-29 Кл·м. Дипольные моменты молекул считать расположенными вдоль соединяющей молекулы прямой.
Задача №10 Диполь с электрическим моментом р=100 пКл·м свободно устанавливается в однородном электрическом поле напряженностью Е=150 кВ/м. Вычислить работу А, необходимую для того, чтобы повернуть диполь на угол α =180.
Задача №11 Определить потенциальную энергию системы четырех точечных зарядов, расположенных в вершинах квадрата со стороной длиной a=10 см. Заряды одинаковы по модулю Q=10 нКл, но два из них отрицательны. Рассмотреть случай когда разноимённые заряды чередуются.
Задача №12 Электрическое поле создано заряженным проводящим шаром, потенциал ϕ которого 300 В. Определить работу сил поля по перемещению заряда Q=0,2 мкКл из точки, расположенной на расстоянии радиуса шара от поверхности шара, в точку, расположенную на расстоянии трёх радиусов от поверхности шара.
Задача №13 Бесконечная пластина из диэлектрика с проницаемостью ε заряжена однородно с объемной плотностью заряда ρ. Толщина пластины равна 2a. Вне пластины ε=1. Направим ось перпендикулярно к пластине. Начало координат поместим в середине пластины. Найдите ϕ и Ех внутри и вне пластины как функцию x. Потенциал в середине пластины положить равным 0. Построить графики ϕ и Ех. Найти поляризованность Р диэлектрика как функцию х, поверхностную плотность σ’ связанных зарядов на левой и на правой границе пластины. Найти объёмную плотность связанных зарядов.
Задача №14 В пространстве, наполовину заполненном парафином (ε=2), создано однородное поле, напряжённость которого в воздухе Е1=2 В/м. Вектор Е1 образует угол α1= 60⁰ с границой раздела парафин-воздух. Определить векторы электрического смещения, напряжённости и поляризации в парафине.
Задача №15 В зазор между разноимённо заряженными обкладками конденсатора ввели параллельно пластину из диэлектрика. Чему равен поток вектора D через замкнутую поверхность произвольной формы, захватывающую часть плоской поверхности диэлектрика и не захватывающую обкладки конденсатора?
З адача
№16 Получить
выражение для ёмкости С сферического
конденсатора. Радиусы обкладок r1
и r2
(r1
< r2).
Зазор между обкладками заполнен
диэлектриком с проницаемостью ε.
адача
№16 Получить
выражение для ёмкости С сферического
конденсатора. Радиусы обкладок r1
и r2
(r1
< r2).
Зазор между обкладками заполнен
диэлектриком с проницаемостью ε.
Задача №17 Первоначально в пространстве между обкладками плоского конденсатора имеется вакуум. В этом случае напряженность поля в зазоре равна Е, а электрическое смещение D. Затем половина зазора заполняется так, как показано на рисунке однородным изотропным диэлектриком с проницаемостью ε. Найти возникающие после этого значения Е1 и D1 в части зазора 1, а также значения Е2 и D2 в части зазора 2. Рассмотреть два случая: а) остается прежним напряжение между обкладками, б) остаются неизменными заряды на обкладках.
Задача №18 Площадь каждой обкладки плоского конденсатора S=1м2, расстояние между обкладками d=5 мм. Зазор между обкладками заполнен двухслойным диэлектриком. Проницаемость и толщина первого слоя ε1=2, d1=3 мм, второго слоя ε2=3, d2=2 мм. Найти ёмкость конденсатора.
З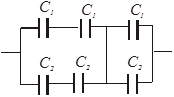 адача
№19 Рассчитайте
общую емкость батареи конденсаторов,
соединенных, как показано на рисунке.
Здесь С1=20
мкФ, С2=10
мкФ. (10 мкФ)
адача
№19 Рассчитайте
общую емкость батареи конденсаторов,
соединенных, как показано на рисунке.
Здесь С1=20
мкФ, С2=10
мкФ. (10 мкФ)
Задача №20 Рассчитайте общее сопротивление проводников, соединенных, как показано на рисунке. Здесь R1=20 Ом, R2=10 Ом. (10 Ом)
З адача
№21 Конденсатор
ёмкости C=300
пФ подключается через сопротивление R
= 500 Ом к источнику постоянного напряжения
U0.
Определить время t,
по истечении которого напряжение на
конденсаторе U=0,99U0.
адача
№21 Конденсатор
ёмкости C=300
пФ подключается через сопротивление R
= 500 Ом к источнику постоянного напряжения
U0.
Определить время t,
по истечении которого напряжение на
конденсаторе U=0,99U0.
Задача №22 Заряд q=1·10-10 Кл равномерно распределён по поверхности шара радиуса r=1см. Диэлектрическая проницаемость окружающей шар среды ε=4. Найти энергию поля, связанного с шаром и энергию взаимодействия системы зарядов на поверхности шара.
Задача №23 Из материала с удельным сопротивлением ρ изготовлено плоское кольцо толщины d. Радиусы кольца равны a и b (b>a). Между внешней и внутренней цилиндрическими поверхностями кольца поддерживается некоторая разность потенциалов. Найти сопротивление R кольца в этих условиях.
З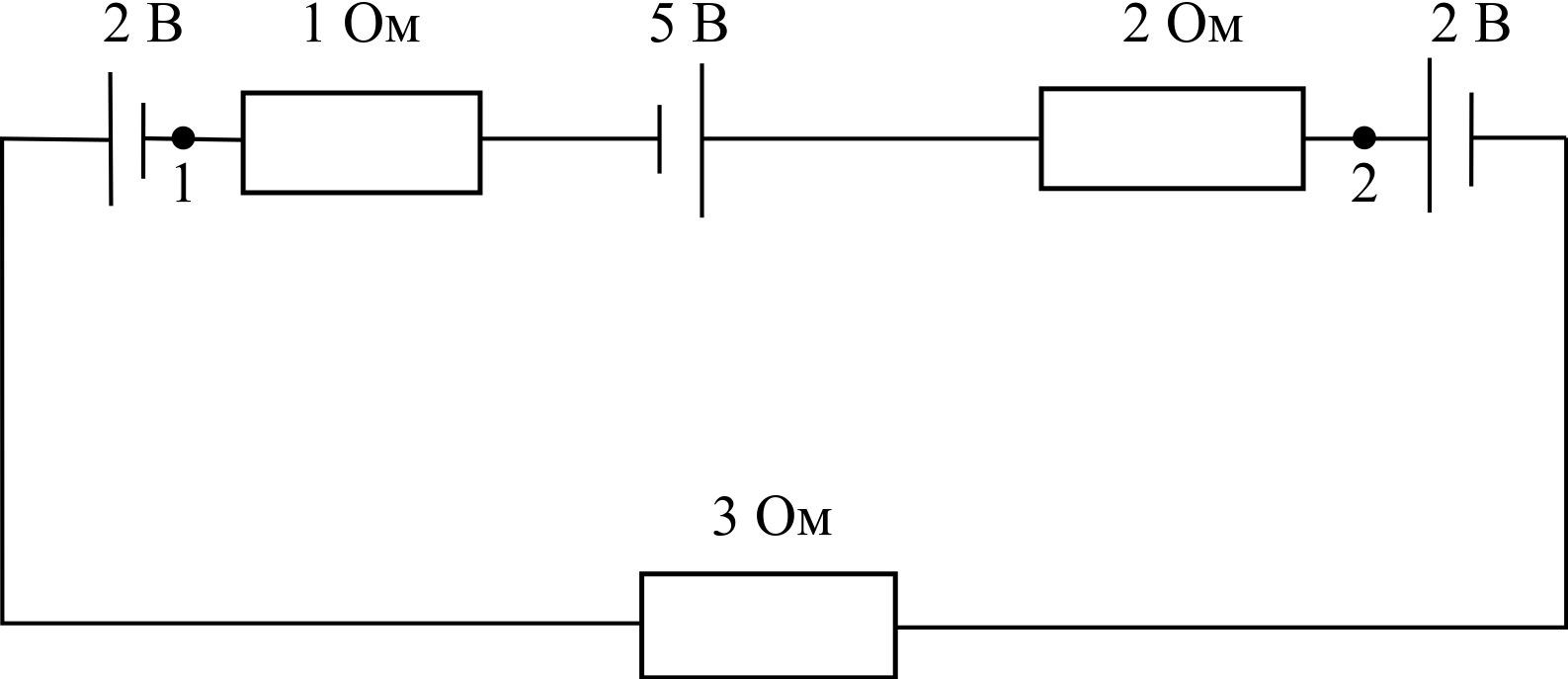 адача
№24 На рисунке
изображена цепь постоянного тока,
состоящая из трех источников тока и
трех сопротивлений, включенных
последовательно. Определить разность
потенциалов φ1-φ2
между точками 1 и 2. Сопротивлением
источников тока и соединительных
проводов пренебречь.
адача
№24 На рисунке
изображена цепь постоянного тока,
состоящая из трех источников тока и
трех сопротивлений, включенных
последовательно. Определить разность
потенциалов φ1-φ2
между точками 1 и 2. Сопротивлением
источников тока и соединительных
проводов пренебречь.
Задача №25 Имеется N = 24 одинаковых источников тока с Ɛ=1 В и внутренним сопротивлением R0=0,2 Ом. Эти источники соединены так, что образуют батарею из n последовательных секций, каждая из которых состоит из N/n соединённых параллельно источников. К батарее подключен прибор, обладающий сопротивлением R=0,3 Ом. При каком n мощность P, отбираемая прибором, будет максимальной? Чему равно максимальное значение P ?
Задача №26 Обкладкам конденсатора ёмкости С=2 мкФ сообщаются разноимённые заряды q0=1 мКл. Затем обкладки замыкаются через сопротивления R=5000 Ом. Найти количество тепла, выделившееся в сопротивлении при разрядке конденсатора. Сравните полученную для расчёта формулу с формулой для энергии плоского конденсатора.
Задача №27 Вольтметр постоянного тока рассчитан на измерение максимального напряжения 3 В. Сопротивление прибора 300 Ом, шкала имеет 100 делений. Какой будет цена деления этого прибора, если его использовать в качестве амперметра? 0,1 мА/дел
З адача
№28 Амперметр
имеет сопротивление 200 Ом и при силе
тока I
=100 мкА стрелка отклоняется на всю шкалу.
Какое добавочное сопротивление надо
подключить, чтобы прибор можно было
использовать как вольтметр для измерения
напряжения 2 В?
19,8 кОм
адача
№28 Амперметр
имеет сопротивление 200 Ом и при силе
тока I
=100 мкА стрелка отклоняется на всю шкалу.
Какое добавочное сопротивление надо
подключить, чтобы прибор можно было
использовать как вольтметр для измерения
напряжения 2 В?
19,8 кОм
Задача №30 В схеме, изображённой на рисунке, Ɛ1=10 В, Ɛ2=20 В, Ɛ3=30 В, R1=1 Ом R2=2 Ом R3=3 Ом R4=4 Ом R5=5 Ом R6=6 Ом R7=7 Ом. Внутреннее сопротивление источников тока пренебрежимо мало. Найти силы токов I1, I2, I3.
З адача
№40 Заряд
q < 0движется
со скоростью
адача
№40 Заряд
q < 0движется
со скоростью![]() .
Укажите направление и сравните модули
магнитной индукции
.
Укажите направление и сравните модули
магнитной индукции
![]() в точках 1
и 2
(
в точках 1
и 2
(![]() и
и
![]() – радиус-векторы соответствующих
точек).
– радиус-векторы соответствующих
точек).
З адача
№41 Заряд
q > 0движется
со скоростью
адача
№41 Заряд
q > 0движется
со скоростью![]() .
Укажите направление и сравните модули
магнитной индукции
.
Укажите направление и сравните модули
магнитной индукции
![]() в точках 1 и 2.
в точках 1 и 2.
З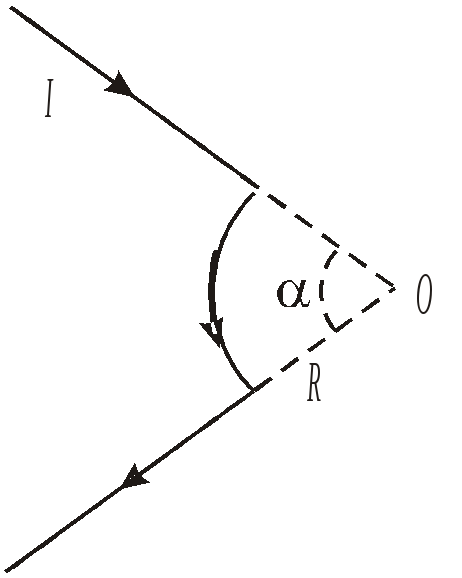 адача
№42 Протон
и электрон, двигаясь с одинаковой
скоростью, влетают в однородное магнитное
поле перпендикулярно его силовым линиям.
Найти отношение радиусов кривизны
адача
№42 Протон
и электрон, двигаясь с одинаковой
скоростью, влетают в однородное магнитное
поле перпендикулярно его силовым линиям.
Найти отношение радиусов кривизны
![]() траекторий частиц, если отношение массы
протона к массе электрона равно
траекторий частиц, если отношение массы
протона к массе электрона равно
![]() .
.
Задача №43 Для проводника, изображенного на рисунке, найдите магнитную индукцию В в точке О. Геометрические размеры и направление тока указаны на чертеже.
З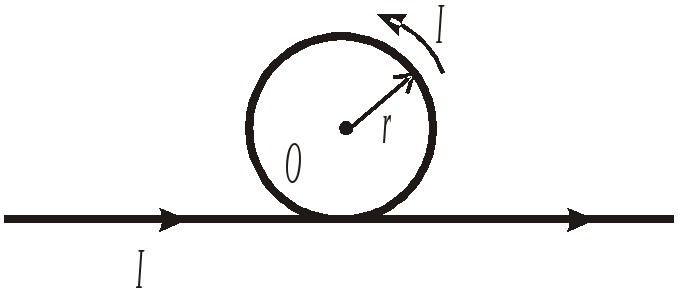 адача
№44 Ток I=1
А течет по бесконечному изолированному
проводнику, имеющему петлю радиусом r
=5 см (см. рис.). Найдите магнитную индукцию
в центре петли. Среда – вакуум. Ответ
выразите в микротеслах. ( 17 мкТл)
адача
№44 Ток I=1
А течет по бесконечному изолированному
проводнику, имеющему петлю радиусом r
=5 см (см. рис.). Найдите магнитную индукцию
в центре петли. Среда – вакуум. Ответ
выразите в микротеслах. ( 17 мкТл)
Задача №45 Рядом с длинным прямым проводом, по которому течёт ток I1=10 А, расположена квадратная рамка с током I2=10 А. Рамка и провод лежат в одной плоскости. Ось рамки параллельна проводу и отстоит от него на расстоянии b=10 см. Сторона рамки a=8 см. Найти силу F, действующую на рамку, и работу A, которую нужно совершить, что бы повернуть рамку вокруг её оси на 180⁰.
Задача №46 Небольшая магнитная стрелка совершает в магнитном поле Земли малые колебания с периодом Т1=8, 92 с. При помещении её внутрь соленоида, по которому течёт ток, стрелка колеблется с периодом Т2=0,68 с. Определить магнитную индукцию B2 поля внутри соленоида. Горизонтальная составляющая индукции земного магнитного поля B1=18 мкТл. Затуханием колебаний стрелки пренебречь
Задача №47 Две небольшие одинаковые катушки расположены так, что их оси лежат на одной прямой. Расстояние между катушками l=2м значительно превышает их линейные размеры. Число витков каждой катушки N=150, радиус витков r=50 мм. С какой силой взаимодействуют катушки, когда по ним течёт одинаковый ток I=1А
Задача №48
По круглому прямому проводу радиуса R
течёт ток одинаковой по всему сечению
плотности
![]() .
Найти выражение для напряжённости поля
.
Найти выражение для напряжённости поля
![]() в
точке, положение которой относительно
оси провода определяется перпендикулярным
к этой оси радиус-вектором
в
точке, положение которой относительно
оси провода определяется перпендикулярным
к этой оси радиус-вектором
![]() .
Рассмотреть случаи, когда точка лежит
внутри и вне провода. Применить теорему
о циркуляции
.
Рассмотреть случаи, когда точка лежит
внутри и вне провода. Применить теорему
о циркуляции
![]() .
.
Задача №49 Две
большие пластины из однородных магнетиков
проницаемостями μ1
и μ2
сложены вместе и помещены в перпендикулярное
к ним однородное поле с индукцией B0.
Чему равны потоки векторов
![]() через цилиндрическую поверхность,
образующие которой параллельны B0,
а основания находятся в разных магнетиках.
через цилиндрическую поверхность,
образующие которой параллельны B0,
а основания находятся в разных магнетиках.
Задача №50 На железном сердечнике в виде тора диаметра d=500мм имеется обмотка с числом витков N=1000. В сердечнике сделана поперечная прорезь, в результате чего образовался воздушный зазор ширины b=1 мм. При силе тока в обмотке I=0.85 А напряжённость поля в зазоре H=600 кА/м. Определить магнитную проницаемость μ железа при этих условиях.
