Ч2-17час-ЭлМагн-ВсеСеминары

Задачи для самостоятельной работы

Задача №1 Два одинаковых проводящих заряженных шара находятся на расстоянии r = 60 см. Сила отталкивания F₁ шаров равна 70 мкН. После того, как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F₂ = 160 мкН. Вычислить заряды Q₁ и Q₂, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.

Задача №2 В вершинах квадрата находятся одинаковые заряды Q=0,3 нКл каждый. Какой отрицательный заряд Q₁ нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

Задача №3 Положительный точечный заряд 50 мкКл находится на плоскости ХУ в точке с радиус-вектором r₀ = 3i + 2j, где i и j — орты осей x и y. Найти модуль и направление вектора напряженности электрического поля E в точке с радиус-вектором r = 9i - 6j. Здесь r₀ и r в метрах.

Задача №4 Находящийся в вакууме очень тонкий прямой стержень длины 2a заряжен с одинаковой всюду линейной плотностью λ. Для точек, лежащих на оси вдоль стержня, найти модуль E напряженности поля как функцию расстояния от центра стержня, обозначить направление вектора E, найти потенциал ϕ.

Задача №5 Пространство заполнено зарядом, плотность которого изменяется по закону ρ=ρ₀/r, где ρ₀ — константа, r — расстояние от начала координат. Найти напряженность поля Е как функцию радиус-вектора r. Исследовать характер линий напряженности. Область вблизи начала координат исключить из рассмотрения.

Задача №6 Электрическое поле создано бесконечной прямой равномерно заряженной линией (λ=0,3 мкКл/м). Определить поток вектора Е через прямоугольную площадку, две большие стороны которой параллельны заряженной линии и одинаково удалены от нее на расстояние r=20 см. Стороны площадки имеют размеры а=20 см, b=40 см.

Задача №7 В вершине куба расположен заряд q. Найти поток вектора Е через каждую грань куба.

Задача №8 Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями σ₁=1 нКл/м² и σ₂=3 нКл/м². Определить напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам. Найти разность потенциалов между пластинами.

Задача №9 Бесконечная пластина из диэлектрика с проницаемостью ε заряжена однородно с объемной плотностью заряда ρ. Толщина пластины равна 2a. Вне пластины ε=1. Направим ось перпендикулярно к пластине. Начало координат поместим в середине пластины. Найдите ϕ и Е_х внутри и вне пластины как функцию x. Потенциал в середине пластины положить равным 0. Построить графики ϕ и Е_х. Найти поляризованность Р диэлектрика как функцию х, поверхностную плотность σ’ связанных зарядов на левой и на правой границе пластины. Найти объёмную плотность связанных зарядов.

Задача №10 В зазор между разноимённо заряженными обкладками конденсатора ввели параллельно пластину из диэлектрика. Чему равен поток вектора D через замкнутую поверхность произвольной формы, захватывающую часть плоской поверхности диэлектрика и не захватывающую обкладки конденсатора

Задача №11 Получить выражение для ёмкости С сферического конденсатора. Радиусы обкладок r₁ и r₂ (r₁ < r₂). Зазор между обкладками заполнен диэлектриком с проницаемостью ε.

З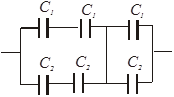адача №12 Площадь каждой обкладки плоского конденсатора S=1м², расстояние между обкладками d=5 мм. Зазор между обкладками заполнен диэлектриком, проницаемость которого изменяется в направлении, перпендикулярном к обкладкам, по линейному закону от значения ε₁=2 вблизи одной обкладки до значения ε₂=5 вблизи другой. Найти ёмкость конденсатора.

Задача №13 Рассчитайте общую емкость батареи конденсаторов, соединенных, как показано на рисунке. Здесь С₁=20 мкФ, С₂=10 мкФ. (10 мкФ)

Задача №14 Из материала с удельным сопротивлением ρ изготовлено плоское кольцо толщины d. Радиусы кольца равны a и b (b>a). Между внешней и внутренней цилиндрическими поверхностями кольца поддерживается некоторая разность потенциалов. Найти сопротивление R кольца в этих условиях.

Задача №15 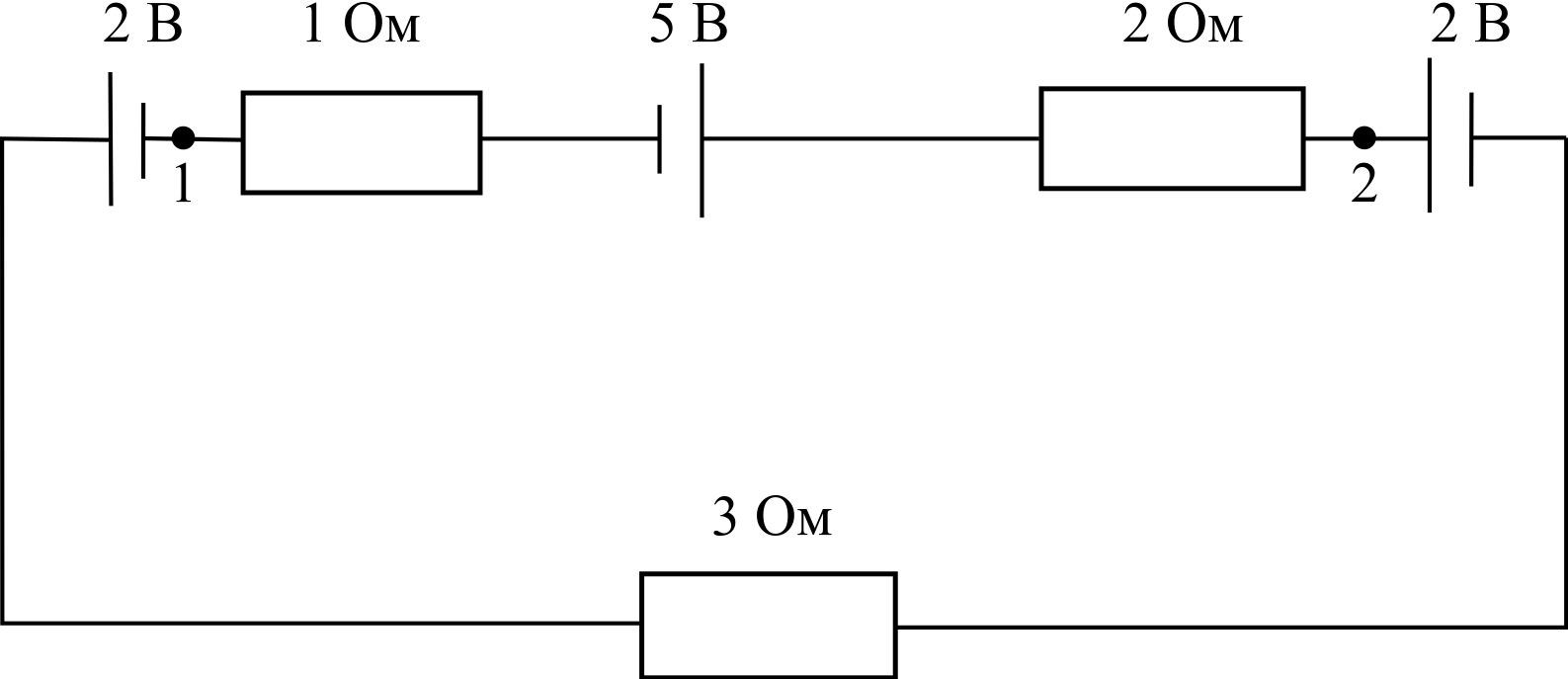На рисунке изображена цепь постоянного тока, состоящая из трех источников тока и трех сопротивлений, включенных последовательно. Определить разность потенциалов φ₁-φ₂ между точками 1 и 2. Сопротивлением источников тока и соединительных проводов пренебречь.

Задача №16 Имеется N = 24 одинаковых источников тока с Ɛ=1 В и внутренним сопротивлением R₀=0,2 Ом. Эти источники соединены так, что образуют батарею из n последовательных секций, каждая из которых состоит из N/n соединённых параллельно источников. К батарее подключен прибор, обладающий сопротивлением R=0,3 Ом. При каком n мощность P, отбираемая прибором, будет максимальной? Чему равно максимальное значение P ?

З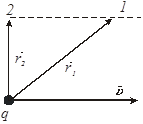адача №17 Обкладкам конденсатора ёмкости С=2 мкФ сообщаются разноимённые заряды q₀=1 мКл. Затем обкладки замыкаются через сопротивления R=5000 Ом. Найти количество тепла, выделившееся в сопротивлении при разрядке конденсатора. Сравните полученную для расчёта формулу с формулой для энергии плоского конденсатора.

Задача №18 Заряд q > 0 движется со скоростью. Укажите направление и сравните модули магнитной индукции в точках 1 и 2 (и – радиус-векторы соответствующих точек).

З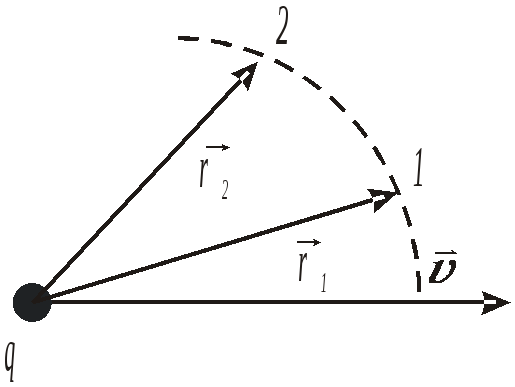адача №19 Заряд q > 0движется со скоростью. Укажите направление и сравните модули магнитной индукции в точках 1 и 2, если эти точки находятся на одинаковом расстоянии от заряда .

З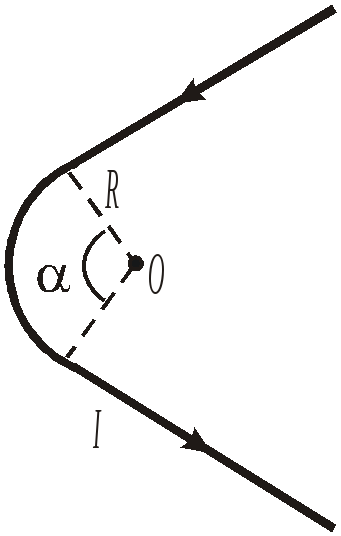адача №20 Протон и электрон, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле перпендикулярно его силовым линиям. Найти отношение радиусов кривизны траекторий частиц, если отношение массы протона к массе электрона равно .

Задача №21 Для проводника, изображенного на рисунке, найдите формулу расчёта магнитной индукции В в точке О. Геометрические размеры и направление тока указаны на чертеже.

З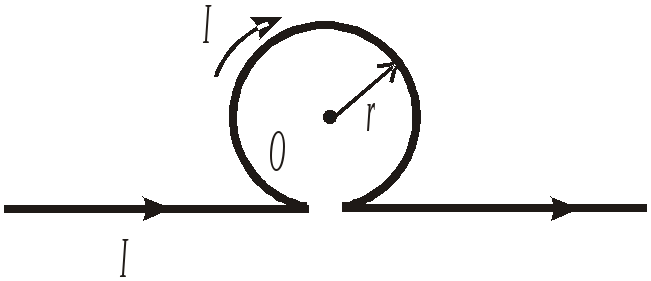адача №22 Ток I = 1 А течет по бесконечному изолированному проводнику, имеющему петлю радиусом r = 5 см (см. рис.). Найдите магнитную индукцию в центре петли. Среда – вакуум. Ответ выразите в микротеслах и округлите до целых. (8 мкТл)