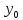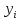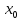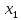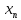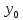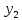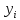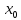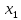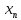Набор лекций по Выч. математике ч 5
.docxРаздел имеет не только самостоятельный интерес, но и имеет существенное значение для решения главных задач вычислительной математики – а именно краевых задач.
Аппроксимация(приближение функций).
Аппроксимирующая(приближенная) функция – это функция, которая с минимальным отклонением описывает другую функцию, заданную следующими способами
-
В виде результатов, расчета на некоторой сходимой функции;
-
В виде результатов расчета по некоторой программе, то есть в виде таблицы;
-
В виде таблицы экспертных данных.
В любом из этих случаев для построения аппроксимации функции мы будем иметь таблицу, которая в одномерном случае будет влиять так. Пусть y = f(x).
|
y |
|
|
|
… |
|
… |
|
|
x |
|
|
|
… |
|
… |
|
a≤ ≤b
≤b
ϕ(x) =
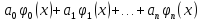
Здесь
 – заданные функции;
– заданные функции;
 -
коэффициенты неизвестны.
-
коэффициенты неизвестны.
Возникают вопросы:
-
Каков критерий минимальности отклонения ϕ(x) - ?;
-
Каков класс функций ϕ(x) - ?;
-
Как определять коэффициенты - ?;
-
Как располагать узлы - ?;
-
Какова погрешность - ?.
Эти вопросы чаще всего связаны друг с другом.
Критерии.
-
Критерий интерполяции. Значения аппроксимационной и заданной функции должны совпадать в узлах: f(
 )
= ϕ(
)
= ϕ( ),
i
=0. Казалось естественно. Однако не в
случае эксперимента данных. Если здесь
требовать совпадения, то мы будем
повторять ошибки эксперимента, поэтому
кроме того
),
i
=0. Казалось естественно. Однако не в
случае эксперимента данных. Если здесь
требовать совпадения, то мы будем
повторять ошибки эксперимента, поэтому
кроме того -
Критерии наименьших квадратов: min
 .
Этот критерий дает возможность
использовать многочлен степени m
<<
n;
.
Этот критерий дает возможность
использовать многочлен степени m
<<
n; -
Критерий наилучшего равномерного приближения
На заданном отрезке
 максимальная величина абсолютного
отклонения должна быть минимальной
максимальная величина абсолютного
отклонения должна быть минимальной
min.max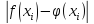 – критерий минимакса.
– критерий минимакса.
Классы функций
Алгебраические функции – в виде полиномов. Тригонометрические функции – sin, cos.
Определение коэффициентов
Часто связано с критерием – например МНК, критерий интерполяции.
Погрешность
Может быть в узлах, между узлами.
Часто при изложении материала различные методы аппроксимации классифицируют исходя из критерия малости отклонения. Мы поступим также, но будем иметь в виду, что в зависимости от некоторых условий один и тот же вид аппроксимирующей функции может удовлетворять разным критериям.
Итак рассмотрим наиболее распространенные, так называемые, интерполяционные многочлены.
Итак пусть функция y = f(x) задана таблицей:
|
y |
|
|
|
… |
|
… |
|
|
x |
|
|
|
… |
|
… |
|
Аппроксимирующую функцию ищем в виде:
ϕ(x)
=

Рассмотрим некоторые характерные(или часто применяемые) аппроксимирующие функции и соответствующие методы.
-
Аппроксимация с помощью алгебраических полиномов Лагранжа. Применяется на основе критерия интерполяции, то есть совпадения в узлах
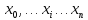
L(x)
=
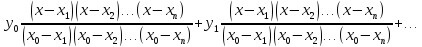
L(x)
=

Роль коэффициентов
играют сами значения функции в узлах,
деленные на произведение скобок. Формула
справедлива для произвольного
расположения
узлов. Когда подставляем x
=
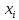 ,
получаем
,
получаем
 ,
то есть имеет место совпадение в узлах.
,
то есть имеет место совпадение в узлах.
-
Аппроксимация с помощью алгебраических полиномов Ньютона. Применяется с использованием критерия интерполяции, то есть требования совпадения в узлах
N(x) =

Неизвестные коэффициенты определяются из критерия интерполяции
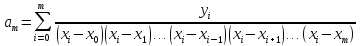
m = 0,1…..n.
Формула справедлива для произвольного расположения узлов. Если будут добавляться новые узлы, ранее рассчитанные коэффициенты не изменяются.
Общие замечания, относительно к L(x) и N(x)
-
При заданном наборе узлов существует один и только один многочлен степени не выше n, принимающий в узлах заданные значения. Форма разная но многочлен один;
-
О погрешности, если заданная в узлах функция – многочлен, то между узлами также будет n+1 совпадение. Если нет, то
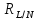 (x)
=
(x)
=

Можно показать,
что эти коэффициенты
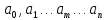 определяются по формуле:
определяются по формуле:
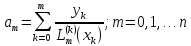
В самом деле мы
видим
 .
Из второго уравнения найдем
.
Из второго уравнения найдем
 :
:
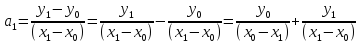
Теперь возьмем
формулу для
 и распишем ее для
и распишем ее для


то есть
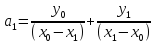 ;
;

Так можно показать
для любого
 .
.
Отметим, что здесь понимается произвольное расположение узлов.
Замечания.
-
Отметим, что как видно из формулы для
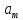 нужно знать только первые m
узлов 1,2…m,
то есть первые табличные данные , а
остальные не нужно. Поэтому добавление
новых узлов не изменяет уже найденные
коэффициенты.
нужно знать только первые m
узлов 1,2…m,
то есть первые табличные данные , а
остальные не нужно. Поэтому добавление
новых узлов не изменяет уже найденные
коэффициенты. -
Очень важное замечание. В силу единственности решения, при заданном наборе узлов существует только один интерполяционный многочлен, разница лишь в алгоритмах его построения(в форме L,H, канонической форме либо другой) и в его форме.
-
Если надо вычислить приближенное значение y при x ≠
 (между узлами), то не надо привлекать
интерполяционный полином, построенный
по всем
узлам.
Достаточно построить полином невысокой
степени по узлам ближайшим к «x».
При этом
(между узлами), то не надо привлекать
интерполяционный полином, построенный
по всем
узлам.
Достаточно построить полином невысокой
степени по узлам ближайшим к «x».
При этом
 можно назвать
можно назвать
 ,
а ближайшие точки слева или справа
узлами
,
а ближайшие точки слева или справа
узлами
 и так далее.
и так далее.
То есть погрешность
зависит от расположения узлов и величины
производной. Например, для функции lnx
производная n
– го порядка приблизительно равна n!
, как будет вести производная функции
неизвестно. Формулой для
 можно узнать.
можно узнать.
Обычно для увеличения точности увеличивают число узлов.
Рунге показал, что
при увеличении «n»;
для функции
 в интервале
в интервале
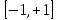 аппроксимирующая функция в интервале
0,7 ≤ x
≤ 1 расходится с заданной.
аппроксимирующая функция в интервале
0,7 ≤ x
≤ 1 расходится с заданной.
Однако если узлы располагать в нулях полиномов Чебышева, то аппроксимирующая функция будет сходиться к заданной. К сожалению это правило действует не для всех непрерывных функций. Безусловно недостатком L и N является рост «n» с числом узлов. И для глобальной интерполяции они мало удобны.
Аппроксимация ортогональными функциями, полиномами Чебышева, тригонометрическими функциями.
Общие понятия:
Система функций
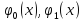 …
… …
…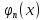 ,
заданная на дискретном множестве точек
,
заданная на дискретном множестве точек
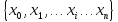 называется ортогональной, если
называется ортогональной, если

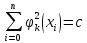
Ряд
 ,
в котором
,
в котором
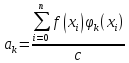 называется рядом Фурье: обычно этот ряд
сходится к f(x).
Здесь для
определения коэффициентов не требуется
применения критерия близости кривых.
называется рядом Фурье: обычно этот ряд
сходится к f(x).
Здесь для
определения коэффициентов не требуется
применения критерия близости кривых.
Полином Чебышева
ϕ(x)
=
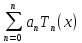 ,
, ;
-1 ≤ x
≤ 1, -1 ≤
;
-1 ≤ x
≤ 1, -1 ≤
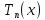 ≤
1
≤
1
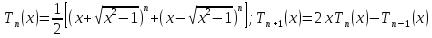

n = 1
 т.д.
т.д.
МНК
Пусть y
= f(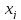 )
задана в узлах j
= 0,1,2…N;
)
задана в узлах j
= 0,1,2…N;
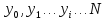 ;
;
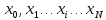
Представим
 .
.
Необходимо найти
такие
 ,
чтобы сумма квадратов отклонений была
минимальна, то есть был min:
Ф =
,
чтобы сумма квадратов отклонений была
минимальна, то есть был min:
Ф =
 .
.
Необходимые условия
минимума:
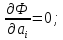
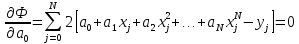

…………………………………………………………………
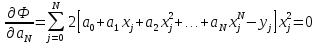
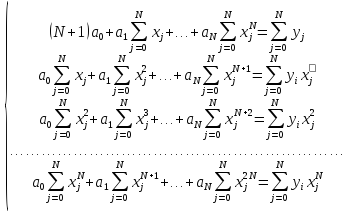
Рассмотрим одно
важное свойство этой системы. Пусть
точки равномерно не расположены на
интервале
 .
В этом случае определитель матрицы:
.
В этом случае определитель матрицы:
det
=
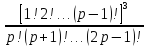 ; где p
= m-1
; где p
= m-1
C
ростом m
величина определителя быстро падает,
так для n
= 1 det
=
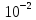 ,
для n
= 2; det
=
,
для n
= 2; det
=
 .
Система становится только обусловленной
и теряется точность. Поэтому при МНК
берут обычно m
≤
3.
.
Система становится только обусловленной
и теряется точность. Поэтому при МНК
берут обычно m
≤
3.
Чтобы повысить «m» используют два приема:
-
Используют систему точек, позволяющих разбить систему уравнений на две подсистемы меньшего порядка
-
используют систему ортогональных многочленов.
Чтобы выбрать
оптимальную степень многочлена строят
многочлен степени n
= 1 и увеличивают его степень до тех пор
пока Ф не станет ~ɛ,
где ɛ - заданная погрешность ( -
средне квадратичное отклонение).
-
средне квадратичное отклонение).
При n = N – совпадение в узлах, но между узлами могут быть отклонения.
При n << N , то приближенный многочлен выбран правильно, если это условие не соблюдается следует искать более удачный вид приближения.
Аппроксимация с применением ортогональных функций(полиномов Чебышева, ортогональных тригонометрических функций)
Общие понятия.
Система базисы функций
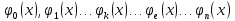 ,
заданная на дискретном множестве
точек(
,
заданная на дискретном множестве
точек(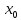 ,
, )
называется ортогональной если
)
называется ортогональной если

Ряд
 ,
в котором
,
в котором

Называется рядом
Фурье. Обычно этот ряд сходится к y
= f(x).
Обычно базисные функции тригонометрические.
Здесь для определителя
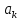 не требуются применения близких кривых.
не требуются применения близких кривых.
Аппроксимация с помощью ортогональных полиномов Чебышева
ϕ(x)
=

-1 ≤ x ≤ 1
-1 ≤
 ≤ 1
≤ 1

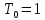 ;
;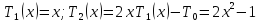 .
.
Соответственно
можно выразить: x
=
 ;
;
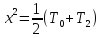 ;
; и так далее.
и так далее.
Пользоваться для случая аналитически заданной функцией(априория оценки).
Если функция задана таблично, то используют апостериорную оценку по первому отброшенному члену многочлена Ньютона.
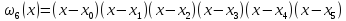
Пример для многочлена
пятой степени. Видно, что
 минимально между точками
минимально между точками
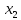 и
и
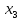 к крайним узлам экстремумы возрастают.
Поэтому первым
способом
уменьшения ошибки при постоянном шаге
является выбор точки x
в близи середины отрезка интерполирования.
к крайним узлам экстремумы возрастают.
Поэтому первым
способом
уменьшения ошибки при постоянном шаге
является выбор точки x
в близи середины отрезка интерполирования.
Другой способ увеличение при постоянном шаге числа узлов, но это не всегда приводит к уменьшению погрешности.
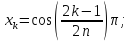 k
= 1,2,…n
k
= 1,2,…n
Если в нулях, то
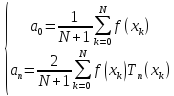
Замечания:
-
Если степень многочлена (или число неизвестных коэффициентов) равна N – числу узлов, то в узлах совпадения, а между узлами равномерное приближение (при узлах в нулях)
Если узлы равномерно – то между узлами выполнение МНК.
-
Если ряд усечь, то есть n < N, то при равномерном расположении узлов, в узлах МНК, можно ожидать что и между узлами, при расположении узлов в нулях Чебышева, то в узлах равномерное приближение, можно ожидать, что и между;
-
Если функция задана в нулях Чебышева, то а) при N -> ∞, погрешность R -> 0; б) Аппроксимационная функция мало чувственна к ошибкам заданной f.
Аппроксимация с помощью ортогональных тригонометрических функций. Ряды Фурье. Пусть f(x) задана на множестве x = 0,1,2,…N-1.
f(x) =
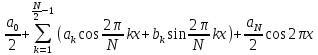
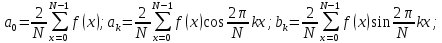
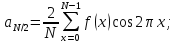
При k = N – совпадение в узлах, между узлами МНК
k < N – в узлах минимум среднеквадратичного отклонения между узлами можно ожидать МНК.
При заданном наборе
узлов – единственность разложения
Фурье. Рунге показал, что при увеличении
«n»;
для функции
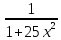 в интервале
в интервале
 аппроксимирующая функция в интервале
0,7 ≤ x
≤ 1 расходится с заданной.
аппроксимирующая функция в интервале
0,7 ≤ x
≤ 1 расходится с заданной.