
- •Математические модели случайных сигналов: функция распределения вероятности и плотность распределения вероятности стохастического сигнала.
- •P.S. В презентациях плотность обозначалась через р, у Щербатого была ω. Обозначайте как хотите, только в дальнейших вопросах не запутайтесь с другой ω.
- •Моментные числовые характеристики закона распределения вероятности: математическое ожидание. Дисперсия, автокорреляционная функция.
- •Стационарные и эргодические случайные процессы.
- •Связь акф с энергетическим спектром случайного сигнала, теорема Винера – Хинчина, интервал корреляции, белый шум.
- •Узкополосные случайные процессы, распределение огибающей и фазы узкополосного случайного процесса.
- •Прохождение белого шума через узкополосную систему.
- •Нормальное распределение, связь корреляции и независимости выборок из нормального случайного сигнала.
Прохождение белого шума через узкополосную систему.
Белый шум. Среди всех источников шума наиболее распространенным на практике и наиболее широко используемым в качестве модели случайного процесса (СП) является шум, описываемый нормальным (гауссовским) распределением.
При прохождении СП с произвольным распределением через узкополосный фильтр (т.е. при ширине полосы пропускания фильтра F существенно меньшей ширины энергетического спектра воздействия fX) наблюдается явление нормализации распределения реакции Y(t). Оно заключается в том, что закон распределения реакции приближается к нормальному. Степень этого приближения тем больше, чем сильнее неравенство F << fX (рис. 5.6).

Рис. 5.6. Спектр широкополосного СП и АЧХ узкополосных ФНЧ и ПФ.
Объяснить это можно следующим образом. В результате прохождения СП через узкополосный фильтр происходит существенное уменьшение ширины его энергетического спектра (с fX до F) и, соответственно, увеличение времени корреляции (c X до Y). В результате между некоррелированными отсчетами реакции фильтра Y(kY) располагается примерно fX /F некоррелированных отсчетов воздействия X(lX),, каждый из которых дает вклад в формирование единственного отсчета реакции с весом, определяемым видом импульсной характеристики фильтра.

Таким образом, в некоррелированных сечениях Y(kY) происходит суммирование большого числа также некоррелированных случайных величин X(lX) с ограниченными математическими ожиданиями и дисперсиями, что в соответствии с центральной предельной теоремой (А.М. Ляпунова) обеспечивает приближение распределения их суммы к нормальному с увеличением числа слагаемых.
Нормальное распределение, связь корреляции и независимости выборок из нормального случайного сигнала.
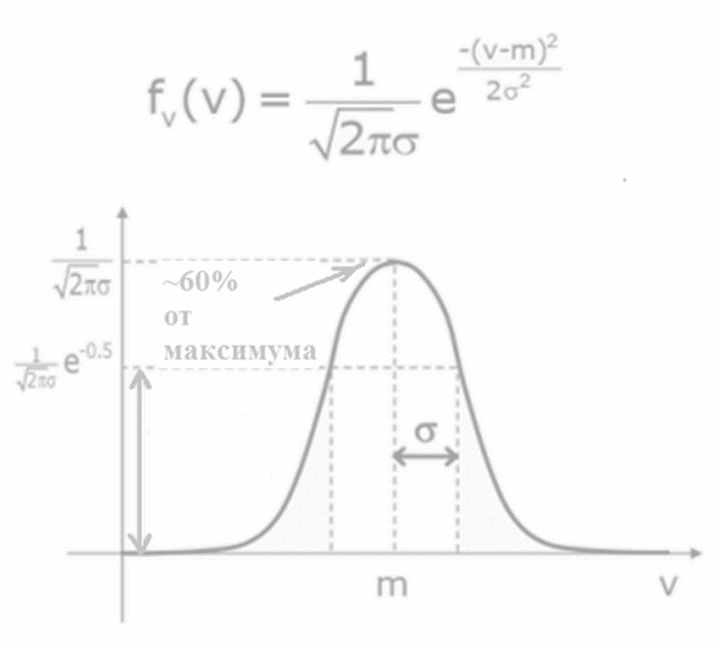
Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
Плотность
вероятности:

где
параметр
 —
математическое ожидание (среднее
значение), медиана и мода распределения,
а параметр
—
математическое ожидание (среднее
значение), медиана и мода распределения,
а параметр
 — среднеквадратическое отклонение (
— среднеквадратическое отклонение ( —
дисперсия) распределения.
—
дисперсия) распределения.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием = 0 и стандартным отклонением =1.
Функция распределения:

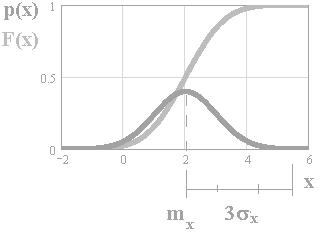
(график из презентации).
Параметры нормальной плотности распределения вероятности
Математическое ожидание (МОЖ)
Среднеквадратическое отклонение от математического ожидания (СКО)
Дисперсия (Квадрат СКО)

Интеграл вероятности
Вероятность, что величина сигнала будет в диапазоне от V1 до V2.
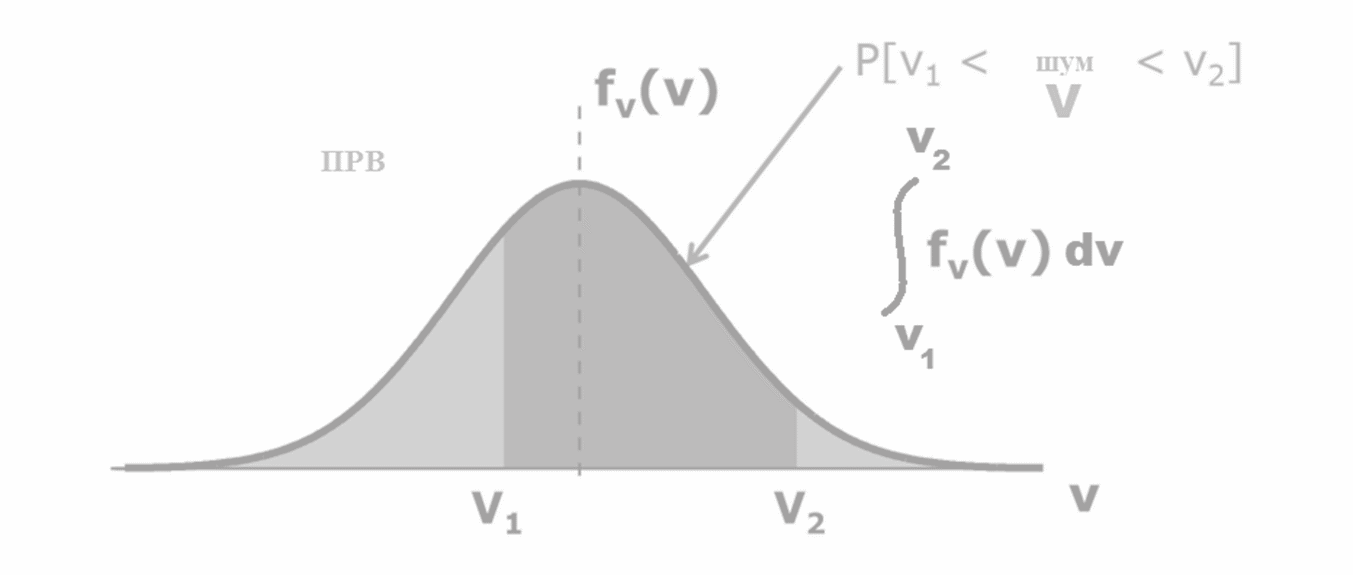
Связь корреляции и независимости выборок из нормального случайного сигнала.

