Меpы сложности алгоpитмов (оценка алгоритмов) Понятие сложности

Для решения одной и той же задачи часто приходится выбирать алгоритм как из числа алгоритмов различных по принципу своей работы, так и из числа возможных реализаций одного алгоритма.

При разных исходных данных за конечное число шагов все они приведут к правильному решению задачи. Но из всего спектра вариантов, следует выбирать наиболее оптимальные.

Когда при решении некоторой задачи есть несколько разных алгоритмов и стоит задача выбора одного из них для реализации, необходима оценка алгоритма с использованием некоторого критерия.

Критерием оптимальности алгоритма выбрана количественная характеристика – сложность алгоритма.

Виды сложностей алгоритма:

• Емкостная (пространственная)

• Временная

• Асимптотическая

Емкостная сложность алгоритма

Под емкостной сложностью (пространственной сложностью, эффективностью) понимают объем памяти, требуемой для выполнения программы. Это функция размера входных и выходных данных.

Но память не является критическим ресурсом для современных ВМ.

Временная сложность алгоритма

Чаще всего под анализом сложности алгоритма понимают исследование времени, необходимого для его выполнения.

Но одна и та же программа при одних и тех же входных данных на разных ПК будет выполняться разное время. Поэтому измерения не могут быть единицами времени (секунды и т.д.).

т.е. физическое время выполнения алгоритма должно зависеть от количества выполняемых в алгоритме команд и времени их выполнения:

i*t, где

i - число действий (элементарных операций, команд),

элементарные операции – это операции, из которых складывается алгоритм решения задачи (:=, <>, =, +, –, *, /; and, or, not, xor; call, return)

t - среднее время выполнения одного элементарного действия, зависит от скорости обработки сигналов ВМ.

Поэтому временная сложность (трудоемкость или вычислительная сложность алгоритма) определяется количеством элементарных операций, совершаемых алгоритмом для решения им поставленной задачи

Временная сложность алгоритма (в худшем случае) - это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, алгоритма.

Количество элементарных операций, зависит не только от размера входных данных, но и от самих данных (например, сортировка вставками, быстрее работает с уже отсортированными данными).

Если размер выхода не превосходит размер входа, то временную сложность можно рассматривать как функцию только размера входных данных.

T(N) - функция временной сложности (трудоемкости) - зависимость времени работы от количества входных данных N – размер задачи.

Однако:

• не всегда ясно, какие операции следует считать элементарными

• разные операции требуют для своего выполнения разного времени

• перевод операций алгоритма в операции, используемые в компьютере зависит от свойства компилятора и квалификации программиста и т.п.

• в ряде случаев неизвестна структура программы

Кроме того, точное значение количества операций, выполненных алгоритмом, не играет существенной роли в его анализе, т.к. не является качественным показателем эффективности алгоритма.

Более важной оказывается скорость роста числа выполняемых операций при возрастании объема входных данных.

Два алгоритма можно сравнить по скорости роста сложности алгоритма.

Скоростью роста сложности алгоритма называется скорость роста числа операций при возрастании объема входных данных.

Именно эта характеристика часто и фигурирует как оценка вычислительной сложности алгоритма.

Поэтому анализ сложности алгоритма предлагается осуществлять, исследуя как меняется время работы программы при увеличении объема входных данных (N) и с какой скоростью.

Вычислительная сложность алгоритмов по-разному зависит от входных данных:

• только от объема данных

• От значений данных

• От порядка поступления данных

• От всех перечисленных выше факторов

Например, многие алгоритмы сортировки потратят гораздо меньше времени на упорядочивание массива, если он уже отсортирован.

Обычно у задачи есть какой-нибудь естественный параметр, характеризующий объем входных данных, и сложность оценивается по отношению к этому параметру

Размер входа определяется для каждой задачи индивидуально.

Например, размером входа принято считать:

• в задачах обработки одномерных массивов - количество элементов в массиве;

• в задачах обработки двумерных массивов - количество элементов в массиве или количество строк и столбцов массива;

• в задачах обработки чисел (длинная арифметика, проверка на простоту и т.д.) - общее число битов, необходимое для представления данных в памяти ВМ;

• в задачах обработки графов - количество вершин графа или число вершин и число ребер графа.

Т.о. время выполнения алгоритма T зависит от объема входных данных N:

T= f (N),

где T – время выполнения алгоритма, мс;

Для построения аналитической зависимости скорости роста:

• оценивают функцию T(N) при некотором интервале [Nmin, Nmax]

• Проводят аппроксимацию этой кривой с помощью некоторой аналитической функции f(N), поведение которой хорошо исследовано

• Изменяют параметры функции и оценивают ошибки аппроксимации.

По виду функции f(N) алгоритмы разделяются на следующие классы:

• С линейной оценкой сложности, если функция f(N) = C· N ;

• С квадратичной сложностью, если

f(N) = C · N ²;

• С полиномиальной сложностью, если

f(N) = C₀ + C₁· N +…+ C_k · N ^k;

• С факториальной сложностью, если f(N) =C· N!;

• С экспоненциальной сложностью, если f(N) = C · a ^N ;

• С гиперэкспоненциальной сложностью, если f(N) = C · a t, где t = a ^N.

Здесь C, a и k = некоторые константы, при этом число C может быть очень большим.

Скорость роста определяется старшим – доминирующим членом формулы.

Отбросив все младшие члены получаем порядок функции или алгоритма.

Эта функция является скоростью роста сложности алгоритма.

Сложность алгоритма	Сложность задачи (кол-во операций)
	10	20	30	40	50	60
N	0.00001сек	0,00002сек	0,00003сек	0,0004 сек	0,0005 сек	0,00006 сек
N2	0,0001 сек	0,0004 сек	0,0009сек	0,0016 сек	0,025 сек	0,0036
N3	0,001 сек	0,008 сек	0,027сек	0,064сек	0,125 сек	0,216 сек
N5	0,1 сек	3,2 сек	24,3 сек	1,7 мин	5,2 мин	13,0мин
2n	0,001 сек	1 сек	17,9 мин	12,7 дней	35,7 лет	366 столетий
3n	0,059 сек	58 мин	6,5 лет	3855 столетий	2*108 столетий	1,3*1013 столетий

Функция временной сложности алгоритма может быть определена точно, но в большинстве случаев искать точное ее значение бессмысленно,

т.к.

• точное значение временной сложности зависит от определения элементарных операций,

• при увеличении размера входных данных вклад постоянных множителей и слагаемых низших порядков, становится незначительным.

Характер поведения временной сложности при увеличении объема данных N (N) называется асимптотической сложностью алгоритма.

Асимптотическая сложность (асимптотическое описание временной сложности) - оценка скорости роста времени работы алгоритмов, предназначенных для решения одной и той же задачи, при больших объемах входных данных.

Именно асимптотическая сложность алгоритма определяет в конечном итоге размер задач, которые можно решать данным алгоритмом.

Чем меньше степень роста, тем больше размер задачи, которую можно решить за фиксированный промежуток времени.

Для описания скорости роста асимптотической сложности используются – нотации.

Говорят, что T(N) - временная сложность алгоритма (время работы алгоритма) – имеет порядок роста f(N), если для T(N) найдётся такая константа С, что, начиная с некоторого N₀, выполняется условие:

T(N) ≤ C*f(N) , функция f(N) неотрицательна при N ≥ N₀.

Или, по-другому, говорят – алгоритм имеет теоретическую сложность O(f(N)):

Т(N) = О(f(N))

O - нотация (нотация Бахмана-Ландау).

Обозначение

Т(N) = О(f(N))

относится к функциям, для которых отношение

T(N)/f(N)→0 (стремится к 0 при росте N).

и означает принадлежность функции Т(N) классу O(f(N)), т.е. функция Т(N) ограничена сверху функцией f для достаточно больших значений аргумента.

Пример 1

Если временная сложность записывается в виде полинома

T(N)=C₁N²+C₂N+C₃,

то такой алгоритм имеет порядок сложности, кратный степени максимального элемента полинома, т. к. он растет наиболее быстро при N:

T(N)=O(N²).

Пример 2:

Функция

f(n) = n²/2 + 3n/2 + 1

 возрастает приблизительно как n²/2 

(отбрасываем сравнительно медленно растущее слагаемое 3n/2+1).

Константный множитель 1/2 также убираем и получаем асимптотическую оценку для алгоритма, которая обозначается O(n²) [читается как "О большое от эн квадрат"].

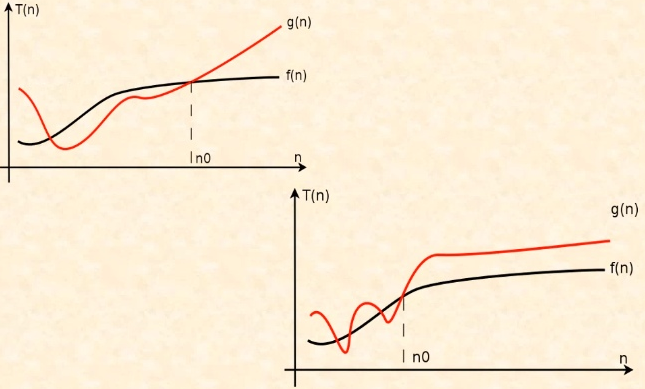
Незначащие члены лишь добавляют “волнистости”, которая затрудняет анализ.

Пример 3:

Пусть Т(0)=1, Т(1)=4, …, Т(N)=(N+1)², тогда временная сложность этого алгоритма имеет порядок роста T(N)= O(N²) = O(f(N)).

Можно показать, что для всех N > n₀ при n₀ = 1, C = 4 выполняется неравенство:

(N+1)²  4*N²

Алгоритмы можно сгруппировать по скорости роста их сложностей.

При анализе алгоритма рассматривается не точное количество выполняемых им операций, а класс скорости роста, к которому относится алгоритм, т.е. общий характер поведения алгоритма, а не подробности этого поведения

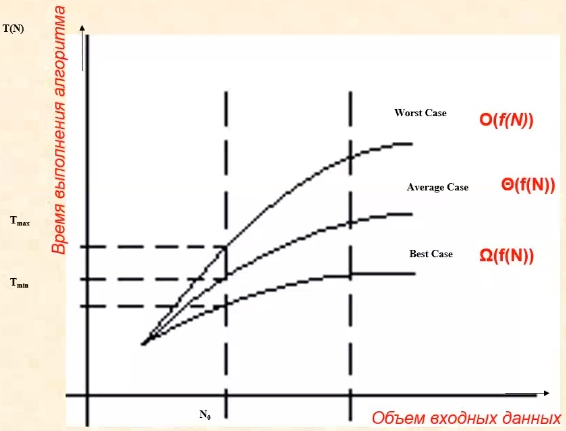
Используются специальные асимптотические обозначения, задающие следующие классы функций:

• класс Ω(f(N) - (читается омега большое) - «лучше не бывает»

• класс О(f(N) - (читается О большое) - «хуже не бывает»

• класс Θ (f(N)) – (читается тета большое) точная оценка - настоящая сложность