Литра / Демирчян, Нейман, Коровкин, Чечурин. Теоретические основы электротехники.т.2.2003

244 Часть 2. Теория линейных электрических цепей

сти. Таким образом, выполненная в настоящем параграфе проверка показывает, что рассматриваемая функция F(p) не имеет нулей и полюсов в правой полуплоскости.

15.7. Синтез входной функции двухполюсника в общем случае. Проверка условия положительности функции Re [F(p)] 0 ïðè Re (p) 0

Проверим другое условие положительности функции Z(p) а именно Re [F(p)] ; 0 ïðè Κ ; 0. Пусть Κ 0, ò. å. p j . Эта проверка сводится к применению следующей процедуры. Выделим вещественную часть рациональной дроби F(p) ïðè p j , ò. å. Re [F(j )]. Нетрудно заметить, что эта часть, как рациональная дробь, должна иметь члены с четными показателями относительно jϑ так как только в этом случае при p j функция будет вещественной. Поэтому представим F(p) в виде суммы рациональных дробей, состоящих из членов с четными и нечетными показателями:

F(p) N (p) M(p).

Òàê êàê

F(p) N 1(p) M1(p) ,

N 2 (p) M 2 (p)

то, перемножив знаменатель и числитель на N2(p) – M2(p), получим

Ïðè p j первый член и окажется вещественной частью N(p) N(j ) функции F(p) F(j ), т. е. он равен величине Re [F(j )], которая должна быть положительной. Знаменатель ее всегда положителен. Поэтому проверка положительности функции N(j ) Re [F(j )] сведется к проверке положительности ее числителя.

Если выполнить операцию N1(j ) N2(j ) – M1(j ) M2(j ), то получим полином от 2. При изменении 2 от нуля до бесконечности значение этого полинома также будет меняться.

Возможны случаи, когда полином при некоторых частотах 2 2k примет

значение, равное нулю. В окрестностях этих точек полином можно представить в виде

P0 ( 2 ) N 1( j )N 2 ( j ) M1( j )M 2 ( j ) ( 2 2k )m f ( 2 ),

ãäå f( 2) — некоторый полином, не равный нулю при 2 2k . Нетрудно заметить, что при 2 2k происходит изменение знака P0 ( 2), åñëè т — нечетное. Таким образом, если имеется нуль полинома нечетной кратности, в том числе простой (m 1), то в этой точке полином P0 ( 2) меняет знак. Если полином P0 ( 2) меняет знак, то это означает, что либо при 2 < 2k , ëèáî ïðè 2 > 2k величина

P0 ( 2) имеет отрицательное значение и, следовательно, функция F(p) не является положительной.

246 Часть 2. Теория линейных электрических цепей

нулю, то они отбрасываются из рассмотрении. В примере, приведенном в таблице, изменение знаков при x x1 происходит пять раз, т. е. число изменений знаков W(x1) 5. Изменение знаков при x x2 происходит три раза, т. е. W(x2) 3.

Теорема Штурма гласит: если действительные числа x1 è x2 (x1 < x2) не являются корнями полинома P0(x), не имеющего кратных корней, òî W(x1) W(x2) и разность W(x1) – W(x2) равна числу вещественных корней (нулей) P0(x), заклю- ченных между x1 è x2.

Полином P0(x), функции Штурма которого принимают знаки, приведенные в таблице, имеет два нуля в интервале x1 < x < x2, и поэтому такой полином не может быть положительным при всех значениях x в этом интервале, т. е. он нереализуем. Полином реализуем только при W(x1) – W(x2) 0.

Подвергнем проверке по этому методу положительность конкретной функции F(p), приведенной в начале предыдущего параграфа.

Числитель вещественной части N(x) этой функции равен

N 1(p)N 2 (p) M1(p)M 2 (p) 80p12 284p10 400p8 287p6 112p4 23p2 2. Ïðè p j имеем p2 – 2, p4 4, p6 – 6, p8 8, p10 – 10, p12 12. Обозначив 2 x, получим

P0 (x) 80x 6 284x 5 400x 4 287x 3 112x 2 23x 2.

Это выражение и будет первой функцией Штурма. Вторая функция Штурма

P1(x) P0 (x) равна P1(x) 480x5 – 1420x4 + 1600x3 – 861x2 + 224x – 23. Разделим P0(x) íà P1(x), заканчивая процесс деления, как было сказано выше.

Получим

Здесь и далее все результаты деления округлены до четвертой значащей цифры.

Третья функция Штурма равна остатку с обратным знаком: P2 (x) 6,694x 4 14,28x 3 10,24x 2 2,922x 0,2681.

Четвертую функцию Штурма находим как остаток с обратным знаком при делении P1(x) íà P2(x):

P3 (x) 20,81x 3 45,48x 2 3180,x 7,133. Пятую и шестую функции Штурма определим аналогично:

т. е. шестая функция Штурма тождественно равна нулю и может быть исключе- на из рассмотрения.

Нас интересует положительность функции во всем диапазоне частот, т. е. для 0 2 . Поэтому возьмем x1 0 è x2 . Тогда знаки функций Штурма будут:

Как видно из таблицы, W(x1) 3, à W(x2) 1, ò. å. W(x1) – W(x2) 2. Поэтому P0(x) имеет на оси x пару корней. Однако это еще не означает, что P0(x) меняет знак. Воспользовавшись известными из алгебры приемами, можно получить

откуда видно, что вещественные корни (нули) этого выражения имеют четную кратность и, следовательно, сама функция P0(x) является положительной, так как при x 0 она положительна. Таким образом, Re [Z(p)]p j ; 0 для всех значе- ний .

Заметим, что в случае, когда существует равенство W(x1) W(x2), получается W(x1) – W(x2) 0. Это указывает на то, что в интервале x1 x x2 рассматриваемая функция не имеет нулей и, следовательно, не меняет знака. В этом случае достаточно установить, что функция положительна в какой-либо одной точке рассматриваемого интервала, чтобы считать ее положительной во всем интервале.

Проверки, приведенные в этом и предыдущем параграфах, показывают, что данная функция F(p) является вещественной и положительной и поэтому реализуема в виде электрической схемы, т. е. можно принять F(p) Z(p) èëè F(p) Y(p).

15.8. Синтез входной функции двухполюсника в общем случае. Реализация заданных функций, имеющих вещественные, мнимые и комплексные корни

В предыдущих параграфах мы убедились, что конкретная функция F(p), приведенная в начале § 15.6, является вещественной и положительной и, следовательно, может быть реализована. Осуществим эту реализацию.

Прежде всего выделим ее части, соответствующие мнимым и вещественным корням числителя и знаменателя, если таковые имеются. Эти выделенные части функции реализуем методами, изложенными в § 15.4 и 15.5. Операцию такого выделения будем производить до тех пор, пока не встретим комплексные корни. При этом придется воспользоваться другим методом реализации, который будет изложен ниже.

Исследуем числитель функции Y2(p) в отношении определения нулей на оси j . Легко заметить, что при наличии нуля на оси j ( p j ) должны быть равны нулю и вещественная, и мнимая части этого числителя, т. е.

причем C3 2, L3 1.

Числитель и знаменатель функции Z4( p) имеют комплексные корни, и поэтому реализация Z4( p) изложенными ранее методами, применимыми, если корни вещественные или мнимые, неосуществима.

Для реализации функции Z4( p) воспользуемся методикой, предложенной Бруне. Прежде всего приведем эту функцию к виду минимального активного сопротивления, т. е. к функции, которая имеет Re [Z( j )] 0 при некоторой часто-

òå 0. Для этого определим минимальное значение Rmin Re [Z4( j 0)], вы- читая которое из Z4( p), получим искомую функцию минимального активного

сопротивления, где Re [Z4( j 0)] – Rmin 0. Ясно, что нельзя вычесть произвольное активное сопротивление, так как при этом можем нарушить условие положительности вещественной части Z4( j ), т. е. получить Re [Z4( j 0)] – R < 0 (если вычесть R > Rmin) или не получить минимальное активное сопротивление (если

R < Rmin), так как при этом ни в одной точке оси j величина Re [Z4( j 0)] – R не примет нулевого значения.

250 Часть 2. Теория линейных электрических цепей

Для определения частоты 0, при которой Re [Z4( j )] min, найдем вещественную часть Z4(j ), используя первый член в правой части формулы (*) в § 15.7:

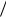
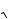
Решение этого уравнения с целью отыскания его действительных корней можно пðîизвести многими методами. Для данного уравнения имеем решение0 12, при котором Re [Z4( j 0)] 1 (ðèñ. 5.16, á). Вычитая Rmin 1 èç Z4( p), не нарушим условие положительности. Находим