Лекции / Переходные процессы в линейных ЭЦ часть 1

Добавил:

Adamant Студент, если у тебя есть завалявшиеся работы, то не стесняйся, загрузи их на СтудентФайлс! Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Петербургский государственный университет путей сообщения им. императора Александра I

Предмет:

Теоретические основы электротехники

Файл:

дующим образом

.pdf

Скачиваний:

Добавлен:

28.09.2020

Размер:

747.02 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

Характеристическое уравнение имеет вид

R L 0 .

Корень характеристического уравнения равен

R L

Выражение для постоянной времени имеет вид:

L R

Чтобы найти постоянную интегрирования А, уравнение (1.9) запишем следую-

щим образом:

До коммутации (

) ток в цепи

	R	t
Ae	L	t
Ae		,

определяется следующим образом:

(1.10)

	i 0	U
	i 0	R
		R

Согласно закону коммутации

	i 0 i 0	U
	i 0 i 0	R
		R

Запишем уравнение (1.10) для момента коммутации и найдем величину А:

U R

Выражение для тока в переходном режиме выглядит следующим образом:

i	U	e	t
i		e

	R

Задаваясь значениями времени по полученному выражению можно по-

строить график тока (рис. 1.4).

По аналогии строится график изменения напряжения на индуктивности во вре-

мя переходного режима (рис. 1.4)

uL L dtdi Ue t .

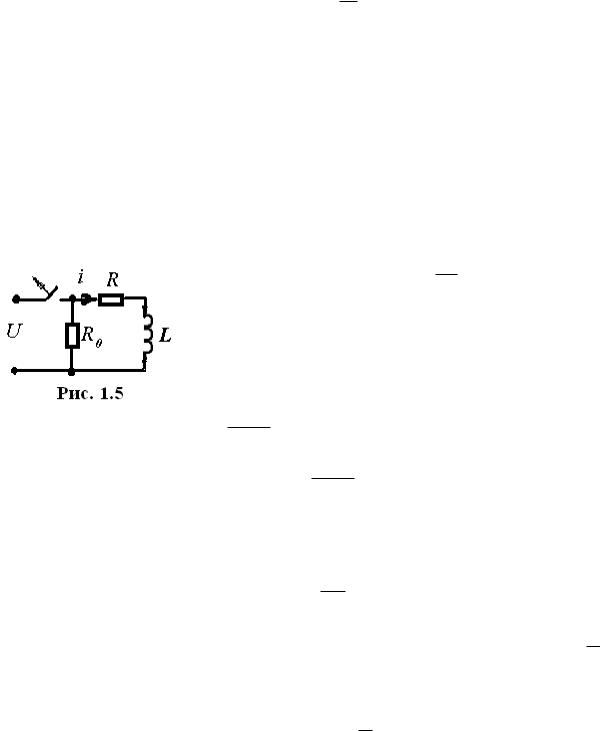
в) Отключение цепи (Рис. 1.5).

Пусть t=0 есть момент коммутации. Составим уравнение цепи после коммутации ( t 0 )

0 R R i L di
0	dt .	(1.11)

Решение уравнения (1.11) ищем в виде:

i i/ i// .

Установившийся ток нового стационарного режима равен Свободный ток ищем в виде

(1.12)

i	/	0 .
	/

i	//	t	.
		Ae

Составим уравнение для свободного тока, пользуясь

R R	i	//
		//
0

уравнением (1.11):

	di	//
L	di		0 .
L	dt		0 .
	dt

Характеристическое уравнение имеет вид:

R R0 L

Корень характеристического уравнения равен

		R R
		0
		0
		L

. Тогда постоянная времени равна

L R R0

Чтобы найти постоянную интегрирования А, уравнение (1.12) запишем следу-

ющим образом:

R R

i Ae

(1.13)

До коммутации ток в цепи определяется следующим образом i 0

Согласно закону коммутации:

i 0 i 0

Запишем уравнение (1.13) для момента коммутации и найдем величину А

0 A,

Выражение для тока в переходном режиме выглядит следующим образом:

	i	U	e	t	.
	i		e		.

		R
Задаваясь значениями времени по полученному выражению можно по-
строить график тока (не приводится).
Напряжение на R0	до коммутации равно						U . При t 0	стало:
	R i 0		U		R0	.
	R i 0		U			.
	0				R
					R
Если R0 R , то напряжение на		R0	при отключении цепи велико. Поэтому

обмотки возбуждения электрических машин (они имеют большую L) снабжа-

ются аппаратами гашения поля. Эти аппараты предохраняют обмотку возбуждения от электрического пробоя.

г). Включение на синусоидальное напряжение, рис. 1

u U

sin t

Пусть t=0 есть момент коммутации. Составим уравнение цепи после

коммутации ( t 0)

u Ri L

(1.14)

Решение уравнения (1.14) ищем в виде:

i i/ i// .

(1.15)

Установившийся ток нового стационарного режима равен

U m

sin t ,

где Z R

L ,

Свободный ток ищем в виде

i// Ae t .

Составим уравнение для свободного тока, для этого в уравнении (1.14)

приравняем нулю приложенное напряжение, в результате получим:

Ri// L di// 0 . dt

Характеристическое уравнение имеет вид:

		R L 0	.
			.
Корень характеристического уравнения равен				R	. Отсюда найдем постоян-
Корень характеристического уравнения равен				L	. Отсюда найдем постоян-
				L
ную времени:	L	.
ную времени:	R	.
	R

Чтобы найти постоянную интегрирования А, уравнение (1.15) запишем следующим образом:

	U		sin t Ae	R	t
i	U	m		L	t	.	(1.16)
i						.	(1.16)

	Z
До коммутации ток в цепи равен i 0 0 .
Согласно закону коммутации:
			i 0 i 0 0 .

Запишем уравнение (1.16) для момента коммутации t 0 и найдем величину А:

0	U	m


	Z

sin

A	U	m


	Z

sin

Формируем выражение для тока в переходном режиме:

i	U	m	sin t


	Z

удвоенной амплитуды установившегося

	U		sin e	R	t
	U	m		L	t	.
						.

	Z
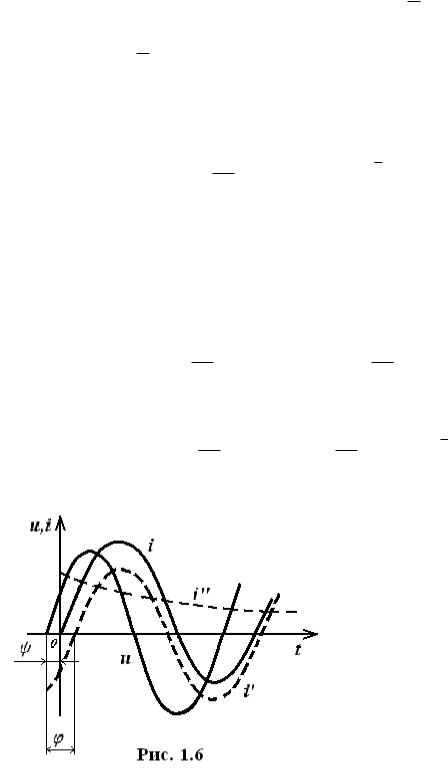
			Задаваясь значениями времени
	по полученному выражению можно
	построить график тока (рис. 1.6).
			Начальное значение свободно-
	го		тока	зависит от				(фазы
	включения). Он принимает макси-
	мальное значение при .
								2
			Наибольшее				значение резуль-
	тирующего				тока		не	превышает
тока.

1.3. Переходные процессы в цепи с последовательно

соединенными R и C

Уравнение цепи в этом случае можно записать следующим образом

u Ri uC .

Так как i

d Cu

, то

u RC

duC

(1.17)

Решение этого уравнения ищем в виде u

u// . Свободную составляющую

представляем, как и в предыдущих случаях, в виде

uC Ae

Составим уравнение для свободной составляющей 0 RC

uC .

Характеристическое уравнение выглядит следующим образом

0 RC 1.

Корень характеристического уравнения равен

, а постоянная времени -

RС

RC .

Выражение для напряжения на конденсаторе определяется так:

uC	uC Аe		t	.
	/
Установившаяся составляющая uC/		зависит от вида приложенного напря-

жения u . Постоянная интегрирования А находится по начальным условиям.

Частные случаи

А). Короткое замыкание (рис. 1.7).

Пусть t=0 есть момент коммутации.

Установившееся напряжение нового стацио-

нарного режима равно uC/ U .

Решение ищем в виде:

										16
u		u	/	u	//	u	/	t
u	C	u	C	u	C	u	C	Ae	.	(1.18)
	C		C		C		C		.	(1.18)

Составим уравнение для свободного напряжения, для этого в уравнении (1.17)

приравняем нулю приложенное напряжение, в результате получим:

	du	//
u RC		C	u	//

	dt			C .

Чтобы найти постоянную интегрирования А, уравнение (1.18) запишем для мо-

мента коммутации

u		0 u	/	0 A
			/
	C		C		.	(1.19)

До коммутации напряжение на конденсаторе определяется следующим обра-

зом: uC 0 U .
Согласно закону коммутации
u	0 u	0 U	.
C	C		.

Из уравнения (1.19) найдем величину А

A U .

Выражение для напряжения в переходном режиме выглядит сле-

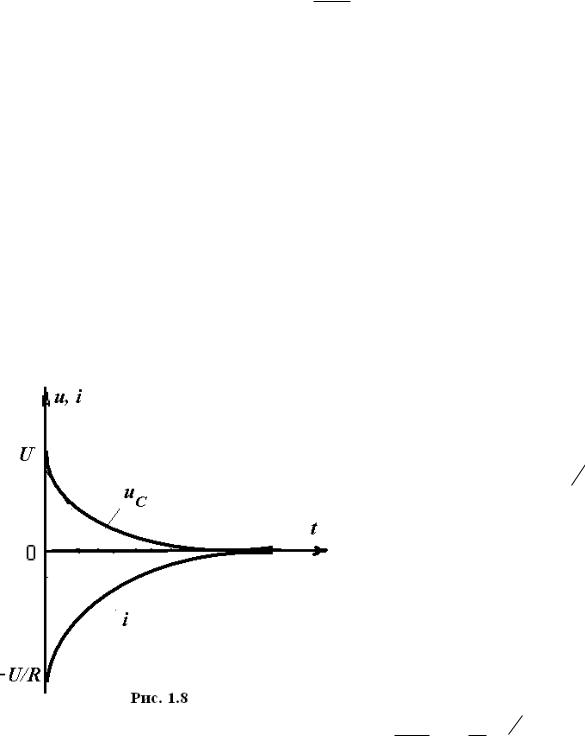
Задаваясь значениями времени по полученному выражению можно построить график напряжения (рис.

1.8).

Используя выражение для тока

i C dudtC UR e t , строится его

график (рис. 1.18).

Во время переходного процесса энергия,

запасенная в электрическом поле конденсатора,

выделяется на активном сопротивлении в виде

тепла. Она равна:

		U	2
Ri	dt	U
2
0		R
0

	2t
e	2t	dt


0

1	CU	2

2

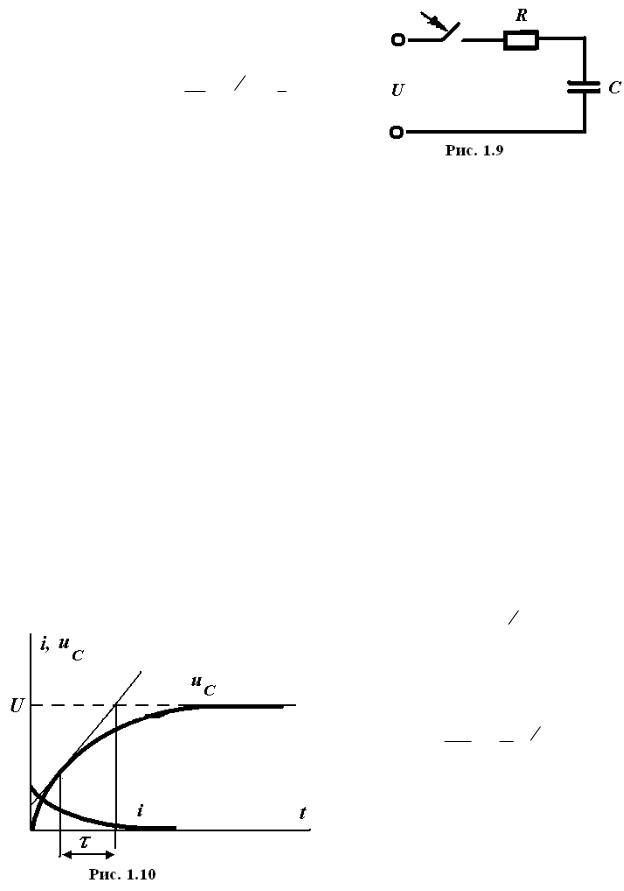
Б). Включение на постоянное напряжение

U (рис. 1.9).

Пусть t=0 есть момент коммутации.
Установившееся напряжение нового стационарного режима равно uC U .
				/
Решение ищем в виде:
uC uC	uC U Ae	t	.	(1.20)
/	//	t

Необходимо рассмотреть два случая.

1. Пусть до коммутации конденсатор не был заряжен, т.е. uC 0 0 .

Согласно законам коммутации uC 0 uC 0 0 .

Решение (1.20) запишем для момента коммутации и найдем постоянную инте-

грирования:

uC 0 uC/ 0 A ,

0 U

A U .

Запишем выражение для напряжения на конденсаторе:

u	C

	t
U 1 e

 

Ток, протекающий по цепи в пере-

ходном режиме, равен

i C	du	C


	dt

U	e	t
	e

R

Во время переходного про-

цесса энергия, запасенная в электрическом поле конденсатора

		duC	U	1
uC idt uC i			dt C duC2		CU 2	,
		dt		2
0	0		0

выделяется на активном сопротивле-

нии в виде теплоты.

2. Пусть до коммутации конденсатор был заряжен: uC 0 uC 0 .

Решение (1.20) запишем для мо-

мента коммутации:

u		0 u	/	0
			/
	C		C

A u	0 U
C

Выражение для напряжения на конденсаторе выглядит следующим обра-

зом:

u		U u	0 U e	t	.
u		U u	0 U e

	C	C

Ток, протекающий по цепи в переходном режиме, равен:

	i C	du
	i C	C
		C
		dt

u	C	0 U	e	t
	C
		R
		R

в). Включение на синусоидальное напряжение

Пусть t=0 есть момент коммутации.

Решение ищем в виде

uC uC/ uC// uC/ Ae t

Установившееся значение напряжения рав-

U	m	sin t	.

(1.21)

	u	/		I	m
но		/			m
но		C		C
		C

где Im				Um		,
где Im						,
				Z
tg			1	.
tg				.
		R C

sin t
Z	R
	2



	1	2
	1	,
		,
	C

Напряжение на конденсаторе во вре-

мя переходного процесса:

uC Im sin t 2 Ae t .C

Пусть до коммутации конденсатор не заряжен uC 0 0 .

Решение (1.21) запишем для момента коммутации и найдем постоянную интегрирования:

0	I	m	sin		A , A	I	m	sin
0			sin		A , A			sin

	C			2		C
	C					C

Найдем выражение для напряжения на конденсаторе:

sin t

sin

Ток, протекающий по цепи в переходном режиме, равен:

i C

Im sin t

sin

Если

свободный ток равен нулю и сразу возникает устано-

вившийся режим. Это связано с тем, что при


		2
		2

напряжение на

конденсаторе в момент коммутации равно нулю, следовательно, и его энергия в этот момент равна нулю.

Если 0 , то свободная составляющая ( uC// ) будет наибольшей и

начальное значение свободного тока равно

	I	m


	RC

. Эта величина при

RC 1

может быть очень большой. Будет иметь место всплеск тока при t=0.

Максимальное значение напряжения на конденсаторе имеет место при

0 и не превышает двойного значения напряжения на конденсаторе в установившемся режиме.

Графики для токов показаны на рис. 1.12.

Продолжение следует…..

Ответить на вопросы по лекции.

1.Что такое коммутация?

2.Что называют постоянной времени переходного процесса?

3.Что характеризует постоянная времени переходного процесса?

4.Какие условия называют независимыми начальными?

<<< < Предыдущая 12 / 22

Соседние файлы в папке Лекции

#
11.07.2020709.13 Кб35Lektsia_Po_Toe_Ot_15_05_2020_Rezonans_Tokov_docx.pdf
#
28.09.2020528.89 Кб34Лекция от 22 апреля Операторный метод расчтета переходных процессов.pdf
#
28.09.2020535.33 Кб41Лекция по ТОЭ интеграл_ Дюамеля от 06.05.2020.docx.pdf
#
28.09.2020775.13 Кб32Лекция по ТОЭ ПП с 2РЭ от 08.04.2020.pdf
#
28.09.2020484.07 Кб37Линейные и нелинейные магнитные цепи.docx
#
28.09.2020747.02 Кб36Переходные процессы в линейных ЭЦ часть 1.pdf