10.5. О расчёте постоянного магнита
Постоянный
магнит представляет из себя кольцевой
стальной сердечник с воздушным зазором
(рис. 10.20). Предположим, что размеры
сердечника lFe,
SFe
и кривая
размагничивания. B(H)
для его
материала задана. Требуется определить
магнитный поток в воздушном зазоре,
если сердечник предварительно намагничен
до насыщения. 
После
намагничивания кольцевого сердечника
без воздушного
зазора
магнитная индукция в нём равна Br,
напряжённость поля равна 0.На петле
гистерезиса (часть кривой приведена на
рис. 10.21) такое состояние соответствует
верхней точке кривой размагничивания
(точка а).
При
наличии воздушного зазора напряжённость
поля в сердечнике не равна 0. В самом
деле, по закону полного тока имеем
 .
(10.1)
.
(10.1) 
Если
lδ<<lFe,
то можно считать Sδ=SFe.
Поэтому

и
из уравнения (10.1) следует
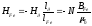 ,
,
где
 - коэффициент размагничивания.
- коэффициент размагничивания.
Отрицательное
значение HFe
означает, что при наличии зазора начальная
индукция снижается по сравнению с
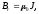 это следует из выражения
это следует из выражения
 .
Так как отрицательному значению HFe
соответствует положительное значение
BFe=Bδ,
то магнитное состояние сердечника
определяется одной из точек кривой
размагничивания (второй квадрант петли
гистерезиса на рис. 10.22)
.
Так как отрицательному значению HFe
соответствует положительное значение
BFe=Bδ,
то магнитное состояние сердечника
определяется одной из точек кривой
размагничивания (второй квадрант петли
гистерезиса на рис. 10.22)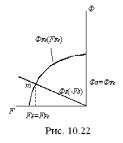
Построим
зависимость
 от МДС в сердечнике
от МДС в сердечнике
 .
Для этого умножим ординаты точек кривой
размагничивания на SFe,
а абсциссы умножим на lFe.
Построим далее зависимость Фδ
от МДС воздушного зазора Fδ.
.
Для этого умножим ординаты точек кривой
размагничивания на SFe,
а абсциссы умножим на lFe.
Построим далее зависимость Фδ
от МДС воздушного зазора Fδ.
 .
.
Отсюда
получаем выражение
 ,
которому соответствует
прямая линия.
,
которому соответствует
прямая линия.
Так
как
 ,
то магнитный
поток определяется ординатой точки
,
то магнитный
поток определяется ординатой точки
 ,
а МДС
,
а МДС
 абсциссой
указанной точки.
абсциссой
указанной точки.



 .
(10.1)
.
(10.1) 

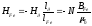 ,
, - коэффициент размагничивания.
- коэффициент размагничивания.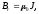 это следует из выражения
это следует из выражения
 .
Так как отрицательному значению HFe
соответствует положительное значение
BFe=Bδ,
то магнитное состояние сердечника
определяется одной из точек кривой
размагничивания (второй квадрант петли
гистерезиса на рис. 10.22)
.
Так как отрицательному значению HFe
соответствует положительное значение
BFe=Bδ,
то магнитное состояние сердечника
определяется одной из точек кривой
размагничивания (второй квадрант петли
гистерезиса на рис. 10.22)
 от МДС в сердечнике
от МДС в сердечнике
 .
Для этого умножим ординаты точек кривой
размагничивания на SFe,
а абсциссы умножим на lFe.
Построим далее зависимость Фδ
от МДС воздушного зазора Fδ.
.
Для этого умножим ординаты точек кривой
размагничивания на SFe,
а абсциссы умножим на lFe.
Построим далее зависимость Фδ
от МДС воздушного зазора Fδ. .
. ,
которому соответствует
прямая линия.
,
которому соответствует
прямая линия. ,
то магнитный
поток определяется ординатой точки
,
то магнитный
поток определяется ординатой точки
 ,
а МДС
,
а МДС
 абсциссой
указанной точки.
абсциссой
указанной точки.