матеша 2 сем экзамен итаэ 1 поток / TeoriaShaposhnikovoy

1. Определение двойного интеграла:

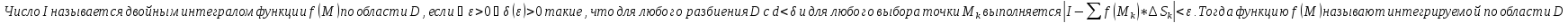
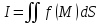
2. Св-ва двойного интеграла:

• Линейность

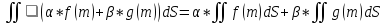
• Аддитивность

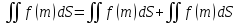
• Интегрируемость неравенств

• Оценка модуля

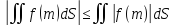
• Площадь плоской фигуры

• Оценка величины интеграла

3. Теорема о среднем значении:

Если 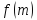непрерывна в замкнутой, связанной, ограниченной области 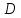, то в 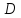найдётся точка , такая что

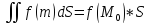
4. Теорема о двух последовательных интегрированиях:

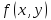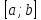Если фун-ия интегрируема в , непрерывны на и существует внутренний интеграл 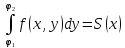, то также существует и повторный интеграл 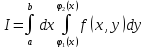и он равен

5. Теорема о замене переменных:

1. Пусть

2. 

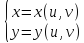
- Отображение взаимнооднозначно;

- Функции непрерывны вместе со своими частными производными;

-

Тогда:

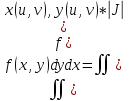
6. Двойной интеграл в полярных координатах:

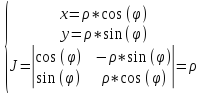
7. Определение тройного интеграла

8. Cв-ва тройного интеграла:

Линейность

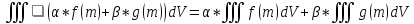
Аддитивность

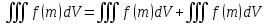
Интегрируемость неравенств

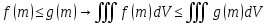
Оценка модуля

Площадь плоской фигуры

Оценка величины интеграла

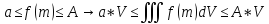
Теорема о среднем значении:

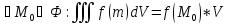
9. Теорема о вычислении тройного интеграла с помощью трёх последовательных интегрирований:

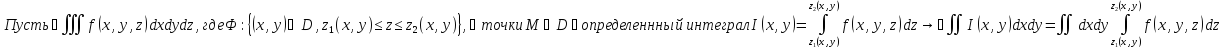
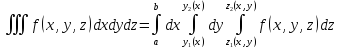
10. Теорема о замене переменных в тройном интеграле:

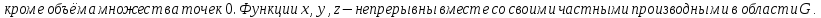
, тогда справедливо

11. Тройной интеграл в цилиндрических координатах.

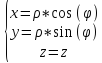
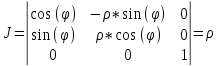
12. Тройной интеграл в сферических координатах

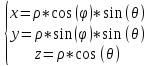
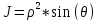
13. Формула Грина:

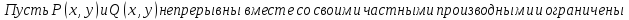
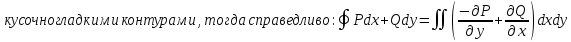
14. Определение потока:

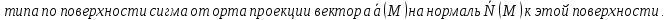
15. Определение дивергенции:

16. Теорема Остроградского – Гаусса:

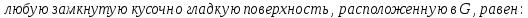
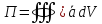
17. Определение циркуляции:

:

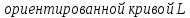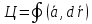
18. Определение ротора:

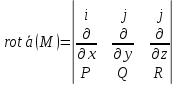
19. Теорема Стокса:

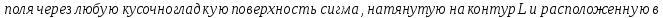
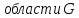
20. Определение потенциального векторного поля:

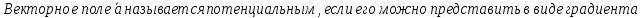
21. Из потенциальности векторного поля следует:

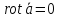
22. Определение соленоидального векторного поля:

23. Из соленоиадальности поля следует, что поток через любую замкнутую поверхность равен 0