
- •Раздел 7. Магнитные цепи
- •7.1. Основные характеристики и свойства магнитного поля
- •2. Магнитная индукция В – силовая характеристика магнитного поля.
- •Или то же уравнение для точки
- •7.2. Магнитные характеристики вещества
- •7.2. Магнитные характеристики вещества
- •Перемагничивание ФММ.
- •7.3. Анализ магнитных цепей с постоянным магнитным потоком
- •Замкнутый контур, который мы обходим проходит вдоль силовой линии магнитного поля. Он охватывает
- •Пример преобразования магнитной цепи в схему замещения
- •3. Для каждого участка магнитной цепи определяем напряженность магнитного поля Н, используя зависимость
- •7.4. Особенности и свойства магнитных цепей при переменном магнитном потоке
- •Примечание: На самом деле МДС никуда не исчезла из магнитной цепи, она важна
- •3. Существуют потери в обмотке и в сердечнике
- •4. Катушка – нелинейный элемент
Раздел 7. Магнитные цепи
Магнитные цепи – один из самых сложных разделов этого семестра и основа для понимания электрических машин. В нашем с вами случае дело осложняется тем, что требуется неплохое знание основ электромагнитных полей из физики. Записать с комментариями все, что я мог бы сказать на лекции нельзя. Поэтому обязательно читайте учебник, может быть, даже физики.
Я дам в лекции только самые-самые основы, фактически, комментарии к учебнику.
Магнитная цепь – это совокупность тел и областей пространства, где сосредоточено магнитное поле.
Магнитная цепь состоит из источников поля и прочих элементов (прочие элементы - ферромагнитные тела и воздушные зазоры).
В магнитной цепи не бывает приемников, подобных резисторам в электрических цепях, т.к. поле нельзя зачерпнуть и потребить. Но поле можно использовать в электромагнитных устройствах для превращения электрической энергии в механическую и обратно, т.к. поле – обязательное условие возникновения взамодействия, приводящего к полезной работе.
Несмотря на кажущуюся разницу между электрическими и магнитными цепями, в них больше общего, чем разного. Физика описывает все электромагнитные явления через систему уравнений Маквелла. Они определяют и электрические, и магнитные поля и явления. Поэтому электрические и магнитные цепи – суть разные стороны одной физической сущности, и не удивительно, что их описание будет схожим. Мы увидим, что существует прямая аналогия между электрическими и магнитными цепями и подходы к анализу магнитных цепей практически те же. Но, естественно, есть и своя специфика. Она в принципиальной нелинейности магнитных цепей, в разной цели анализа магнитных цепей по сравнению с электрическими цепями (в электрических важно найти ток и мощность устройств- двухполюсников, а в магнитных – обеспечить нужное поле в нужном месте, т.е. подобрать источник) и поэтому несколько разном подходе к анализу.
7.1. Основные характеристики и свойства магнитного поля
Основных характеристик магнитного поля три:
•Н (А/м) – напряженность магнитного поля.
•В (Тл) – магнитная индукция
•Ф (Вб) – магнитный поток
1. Напряженность магнитного поля Н |
|
Закон полного тока |
или |
|
Сумма произведений Н l вдоль любого замкнутого контура равна сумме токов, охваченных этим контуром. Здесь l – длина участка контура, Н- напряженность на этом участке.
Отсюда следует, что Напряженность магнитного поля Н характеризует источник магнитного поля – полный ток.
Важно: источником поля является ТОК! Даже в постоянном магните существуют спиновые токи, создающие поля доменов. Но на примитивном уровне можно считать постоянный магнит за источник магнитного поля.
Вторая формулировка уравнения характеризует поле в точке (первая содержит интеграл, а интеграл – всегда усреднение, в нашем случае по контуру). Ротор Н равен сумме векторов плотности тока. Ротор – оператор, показывающий форму поля. Если ротор равен нулю, поле незамкнуто (как поле электрического заряда), а если ротор не нулевой, это означает, что линии поля замкнуты! Если вы ткнули в точку, где тока нет, то в этой точке поле не замкнуто (это кусочек какой-то линии), а если попали в точку, где есть ток, то поле там замкнутое.
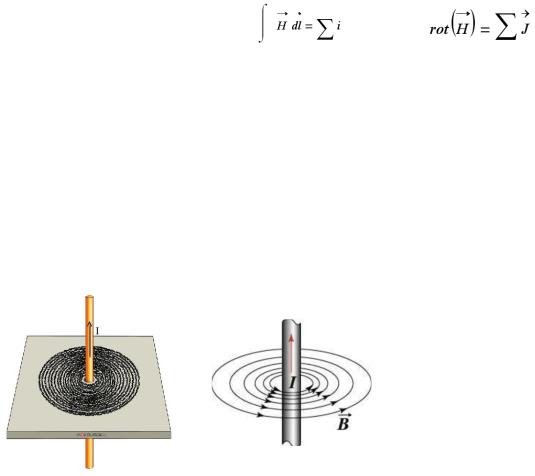
Т.е. закон полного тока выражает математически известную еще из школы картинку: металлические опилки, окружающие проводничок с током, группируются концентрическими окружностями вокруг проводника, а линии поля – концентрические окружности. Направление поля можно определить правилом правого винта или буравчика.
Главное: магнитное поле создается током, магнитное поле всегда замкнуто вокруг проводника с током.

2. Магнитная индукция В – силовая характеристика магнитного поля.
Силовая потому, что все силы зависят от индукции, а не от напряженности. Индукция зависит от напряженности (т.е. от источника поля – тока) и от магнитных свойств среды, в которой происходит взаимодействие.
Сила Лоренца Сила Ампера
Что физика говорит об индукции….
Дивергенция характеризует мощность источника поля (или его сток). Получается, что мощность источника поля всегда и везде равна нулю! Т.е. нет источника магнитной индукции, не существует точки, из которой исходили бы линии магнитного поля (или: не существует магнитных зарядов). Это естественно, раз линии поля Н замкнуты.
Вторая интегральная формулировка. Интеграл B ds (поток) через любую замкнутую поверхность равен нулю. Сколько линий поля вошло через замкнутую поверхность, столько же должно и выйти, раз поле замкнутое и не может выйти из точки или утечь в точку. (Кстати, аналогия с суммой токов в узле!)
3. Магнитный поток Ф
Индукция и напряженность характеризуют поле в точке. Но точечными характеристиками не удобно описывать целые устройства, т.к. поля распределены в пространстве. Поэтому используют поток, он дает представление о среднем поле внутри, например, сердечника трансформатора или электрической машины или катушки с током (кстати, индуктивность катушки L = Ф / I).
Закон электромагнитной индукции: если есть переменный магнитный поток через контур, на зажимах контура возникнет ЭДС.
(Эта ЭДС и есть причина появления напряжения на катушке индуктивности на переменном токе. Чем выше частота тока, тем больше при том же токе напряжение, что в цепях эквивалентно увеличению реактивного индуктивного сопротивления)
Или то же уравнение для точки |
Переменное электромагнитное |
Переменное электромагнитное |
|
поле между магнитопроводами |
поле между обкладками |
|
|
конденсатора |
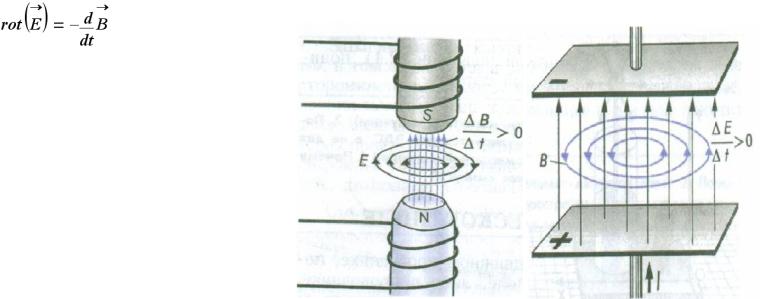
Следствие: переменное магнитное поле порождает вихревое электрическое (справедливо и обратное утверждение), причем, поля В и Е перпендикулярны друг другу.
Если создать переменное магнитное поле в электропроводной среде, то вихревое поле Е (т.е. поле, линии которого замкнуты) создаст силу Кулона и электроны начнут двигаться по таким же замкнутым линиям, как и Е. Это вихревой ток (или ток Фуко), нагревающий все магнитопроводы, греющий кастрюли и сковородки на индукционной плите. Отчасти нечто похожее происходит и в микроволновках, хотя там эффект не только от электропроводности
Итоги напоминания о магнитном поле, которые мы будем использовать и не только в этом семестре:
1.Напряженность магнитного поля характеризует источник поля – электрический ток.
2.Магнитное поле зависит не только от напряженности, но и от магнитных свойств среды.
3.Силовой характеристикой магнитного поля является магнитная индукция: она определяет силу, действующую на движущиеся заряды (электрический ток) в магнитном поле.
4.Магнитное поле всегда замкнуто: нет источника или приемника магнитного поля.
5.Поток через замкнутую поверхность равен нулю.
6.Переменное магнитное поле порождает вихревое электрическое поле и, следовательно, электродвижущую силу (ЭДС), если в поле есть заряд.
7.Полная ЭДС в контуре, находящемся в переменном магнитном поле, определяется скоростью изменения магнитного потока через контур.
7.2. Магнитные характеристики вещества
Все вещества
Диамагнетики |
|
|
|
Парамагнетики |
|
Ферромагнетики |
|
||
|
|
|
|
|
|
|
|
|
|
В электротехнике применяются ферромагнетики. Диа и парамагнетики имеют проницаемость порядка 1, в то время как ферромагнетики – до сотен тысяч.
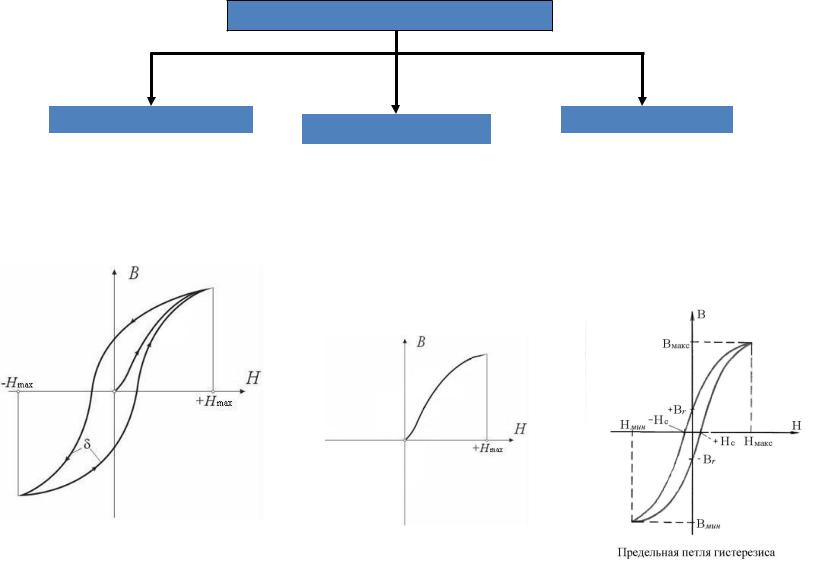
Основная характеристика ферромагнитного материала (ФММ) – зависимость В(Н), а не магнитная проницаемость!
Обычно приводят кривую намагничивания и предельную петлю гистерезиса
Кривая намагничивания
7.2. Магнитные характеристики вещества
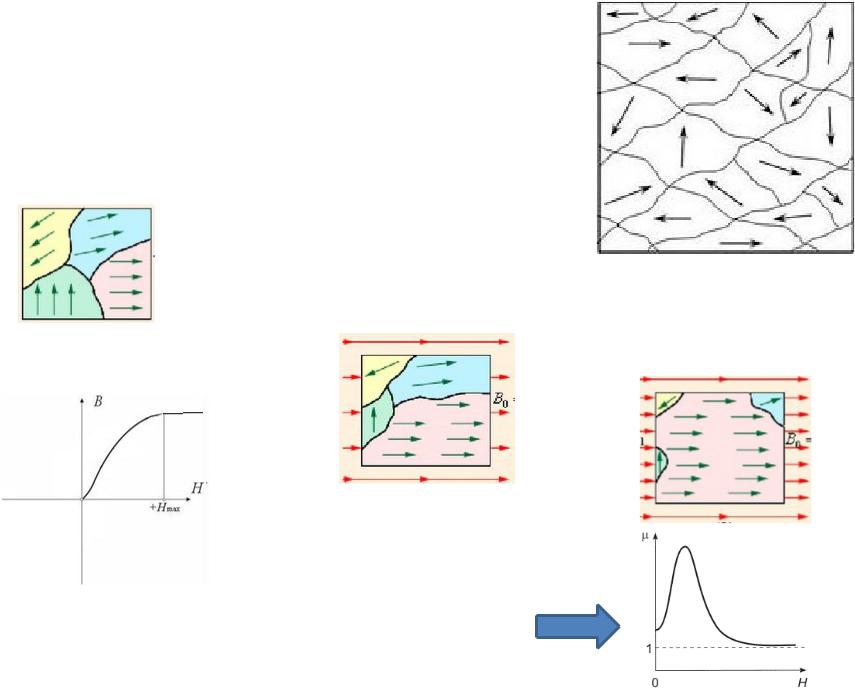
Кривая намагничивания и петли гистерезиса объясняются структурой ферромагнетиков. ФММ состоят из доменов – микрообластей с единым магнитным полем (по сути, микроскопические постоянные магниты размером менее 1 мкм). Сразу после кристаллизации вещества домены расположены хаотично, поэтому в отсутствии внешнего поля (Н) индукция поля внутри ФММ В равна нулю.
Если приложить внешнее поле Н, то на домены- постоянные магниты начнет действоать сила, поворачивающая их вдоль внешнего поля. Из-за трения, не все домены повернутся, а только часть, но очевидно, что результирующее поле ФММ станет больше нуля и сложится с внешним полем, поэтому индукция вырастет не пропорционально полю Н.
Н=0, В=0
Если увеличивать внешнее поле Н, когда-нибудь (при Нmax) все домены
повернутся вдоль поля и прирост индукции за счет ФММ прекратится, достигается насыщение
При напряженностях выше напряженности Нmax рост индукции с ростом напряженности происходит пропорционально 0, как у немагнитных материалов.
Из-за кривизны кривой намагничивания оказывается, что нет какого-то единого значения . Проницаемость зависит от приложенного поля.
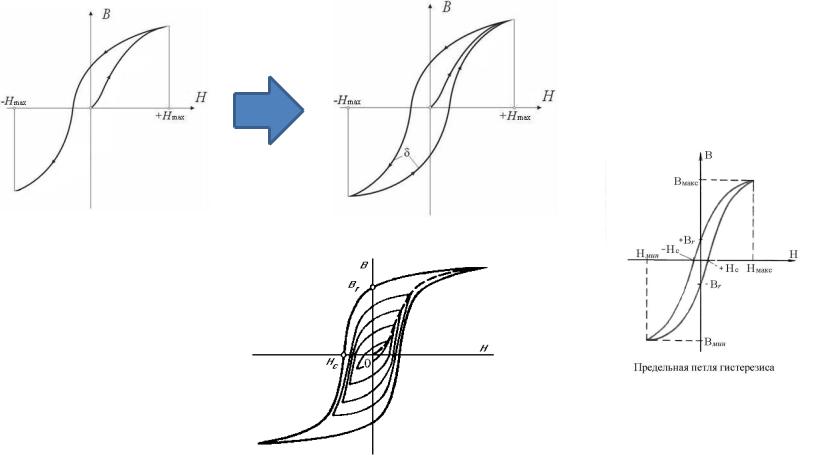
Перемагничивание ФММ.
Петлю гистерезиса при перемагничивании объясняет все та же доменная структура. Если намагниченный до насыщения ФММ унести извнешнего поля, окажется, что индукция не ноль. Потому что из-за трения многие домены не возвращаются в исходное состояние, а остаются ориентированы по ранее приложенному полю. Только если поместить ФММ в поле противоположной полярности, домены начнут поворачиваться и поле будет отрицательным. Намагничивание в отрицательную область проходит аналогично намагничиванию в положительную. Разница с кривой намагничивания в том только, что через начало координат кривые не проходят.
ФММ не обязательно намагничивать до насыщения. Существуют множество частных петель, но ФММ характеризуется предельной петлей, т.к. только она одна постоянна. С частной петли можно легко «уйти» чуть увеличив максимальную напряженность при перемагничивании.
Предельная петля гистерезиса характеризуется:
•коэрцитивной силой Нс
•индукцией насыщения Bmax
•напряженностью насыщения Hmax,
•остаточной индукцией Br
Площадь петли гистерезиса характеризует потери энергии на перемагничивание ФММ. Потери объясняются трением между доменами и выделяются в виде нагрева ФММ.
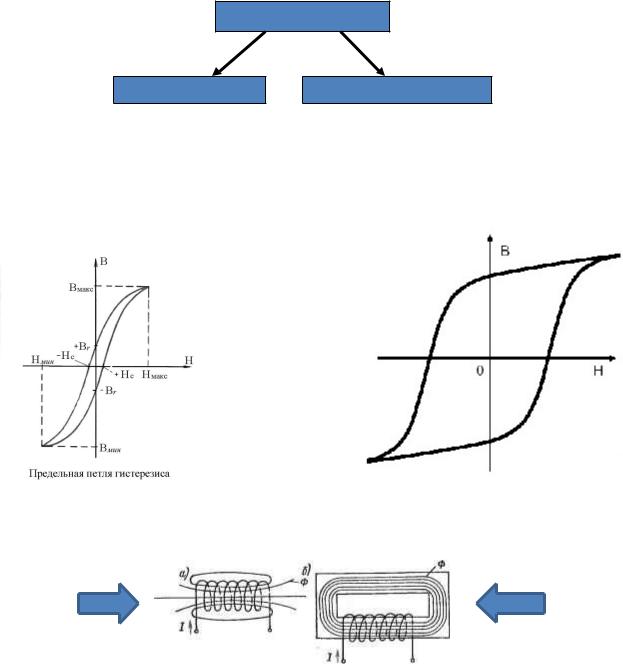
ФММ
Магнитомягкие
Легко перемагничиваются, имеют малую остаточную индукцию и коэрцитивную силу (железо, чугун, элетротехнические стали).
Используются в переменных и постоянных магнитных полях.
Магнитотвердые
Трудно перемагничиваются, имеют большую остаточную индукцию и коэрцитивную силу (постоянные магниты). Используются в постоянном магнитном поле.
Отличительной особенностью всех ФММ является способность концентрировать в себе магнитное поле. Благодаря этому их применяют в качестве магнитопроводов для концентрации магнитного поля в нужном объеме.
Поле катушки без |
Поле катушки с |
|
магнитопровода |
||
магнитопроводом |
||
|
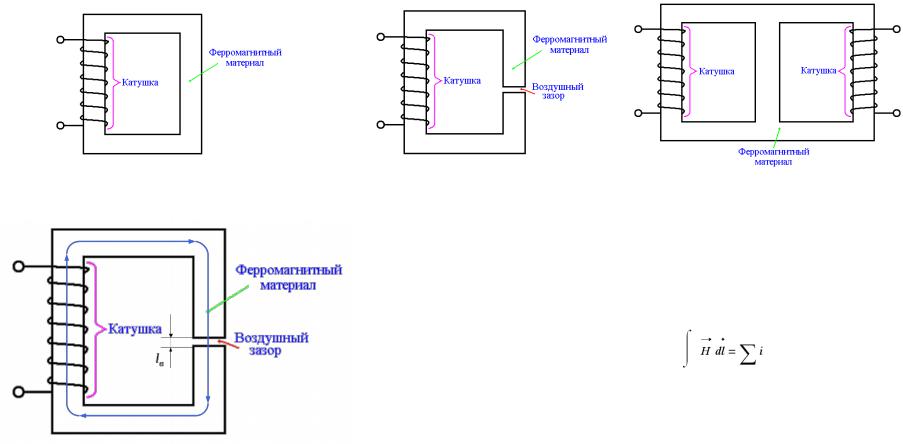
7.3. Анализ магнитных цепей с постоянным магнитным потоком
Классификация магнитных цепей. Цепи бывают:
•однородными / неоднородными
•разветвленными / неразветвленными
Однородная цепь: вдоль силовой линии |
Неоднородная цепь: вдоль силовой линии |
Разветвленная цепь |
магнитный свойства одинаковы |
магнитный свойства различаются |
|
Анализ простейшей магнитной цепи
Источником поля является катушка с током I, имеющая w витков. Поле сконцентрировано в магнитопроводе сечением S и длиной lфмм по средней линии. В магнитопроводе есть воздушный зазор, причем lв много меньше поперечного размера магнитопровода (это
условие необходимо, чтобы избежать нелинейных эффектов «выпучивания» магнитного поля в зазоре и ненужного усложнения расчетов).
Расчет ведут по закону полного тока:
Для простой геометрии можно интеграл заменить суммой:
n
Hk lk I
1

Замкнутый контур, который мы обходим проходит вдоль силовой линии магнитного поля. Он охватывает ток I w раз. Проходит он по сердечнику с длиной lфмм и зазору длиной lв.
F = w ∙I – магнитодвижущая сила (МДС) – причина появления магнитного поля в магнитной цепи.
F = Нфмм lфмм + Нв lв
Магнитный поток в первом приближении одинаков по всей магнитной цепи (при малости воздушного зазора по сравнению с другими размерами магнитной цепи, поэтому целесообразно выразить напряженности через него, используя выражения Ф=В S и B= 0 H:
Здесь видна аналогия между магнитными и электрическими цепями:
Магнитное сопротивление участка цепи |
соответствует электрическому сопротивлению |
||||||
Магнитный поток Ф соответствует электрическому току. |
|
|
|
|
|
|
|
МДС F соответствует ЭДС |
|
|
|
|
|
|
|
|
|
n |
k |
|
|
м |
|
Уравнение |
можно переписать в виде |
|
U |
F |
|||
|
Ф R |
|
|
||||
|
|
1 |
|
|
|
|
|
где Uм – магнитное напряжение, и мы увидим второй закон Кирхгофа! В замкнутом контуре сумма магнитных напряжений равна сумме МДС.
Т.к. через любую замкнутую поверхность магнитный поток равен нулю, можно сформулировать и аналог первого закона Кирхгофа: в узле магнитной цепи сумма магнитных поток равна нулю. Этот закон справедлив для разветвленных цепей.
Таким образом расчет магнитных цепей постоянного потока можно вести с помощью схем замещения аналогично электрическим цепям.
Ранее я обращал внимание на то, что магнитные и электрические явления описываются одинаковыми уравнениями, поэтому не удивительно, что и результат нашего анализа получился схожим. Кстати говоря, уравнения течения жидкости и теплопередачи аналогичны уравнениям Максвелла, поэтому существует аналогия между тепловыми и электрическими процессами, в теплотехнике так же можно встретить поток (но тепловой), сопротивление (термическое), а в качестве источника ЭДС там фигурирует разница температур (электрический потенциал – эквивалент температуры). До развития математического моделирования тепловые процессы и течение жидкости очень часто моделировалось с помощью электрических цепей.
