
- •Зависимости от времени
- •Решение ищется так же в виде суммы свободной и принужденной составляющих и после
- •6.4. Переходный процесс в RLC-цепи
- •Раздел 7. Магнитные цепи
- •7.1. Основные характеристики и свойства магнитного поля
- •2. Магнитная индукция В – силовая характеристика магнитного поля.
- •Или то же уравнение для точки
- •7.2. Магнитные характеристики вещества
- •7.2. Магнитные характеристики вещества
- •Перемагничивание ФММ.

Зависимости от времени |
Ток через конденсатор. |
||||
Напряжение на конденсаторе |
i |
E uc |
|
(UC 0 E) |
e t / |
R |
|
||||
|
|
|
R |
||
Чем больше , тем дольше идет переходный |
Ток может изменяться скачком. Скачок |
|
тока определяется разностью |
||
процесс. Если время пронормировать по , мы |
||
напряжений UC0 – E и сопротивлением R. |
||
получим совпадающие для разных кривые. |
||
Чем меньше R, тем выше скачок тока! (и, |
||
Длительность переходного процесса считают |
||
равным 3 . За это время свободная |
следовательно, быстрее проходит |
|
составляющая убывает в е3 раз. |
переходный процесс) |
Напряжение конденсатора всегда начинается
из Uc0 и стремится к Е. 6.3. Переходный процесс в RL-цепи
|
|
|
uL uR E |
После замыкания ключа уравнение цепи имеет вид |
|||
di |
|
Начальное и конечное условия: |
|
L dt |
i R E |
При t=0 (з-н |
i(0) I0 |
|
|
коммутации) |
i E / R |
|
|
|
|
При t =

Решение ищется так же в виде суммы свободной и принужденной составляющих и после всех манипуляций выглядит так: i iсв iпр (I0 - E/R) e t / E / R
Постоянная времени = L / R. |
|
|
|
Временные зависимости |
Напряжение катушки |
|
|
uL E i R (E - I0 |
R) e t / |
||
|
В отличие от тока, напряжение катушки может изменяться скачком. Этот скачок тем больше, чем больше разность E-I0R.
При больших R скачки напряжения могут значительно превышать ЭДС источника.
Физически напряжение на катушке – это ЭДС
Примечателен процесс размыкания катушки с током. Токсамоиндукции,через катушкувызванноене мож тпеременнымменяться скачтоком,. а при размыкании мы разрываем цепь и очевидно, что ток падает до нуля.
С т.зр. переходных процессов размыкание цепи эквивалентно замыканию на резистор бесконечного сопротивления. Поэтому постоянная времени = L/R = 0. Однако, одновременно с этим возникает скачок напряжения, равный бесконечности. За счет него накопленная энергия катушки падает до нуля за бесконечно малое время. В жизни такого не бывает. Размыкание катушки вызывает оооочень
большое напряжение, которое приводит к пробою контактов ключа. Возникает искра (что раньше использовалось в свечах зажигания автомобилей).
Вообще-то размыкание катушек – очень опасное дело, и двигатели (и другую мощную индуктивную нагрузку) никогда просто так не отключают. Сначала напряжение снижают до нуля, а потом размыкают
контакты.

6.4. Переходный процесс в RLC-цепи
Переходные процессы в RLC цепях примечательны тем, что конденсатор и катушка могут обмениваться энергией друг с другом в ходе переходного процесса. Вспомнить хотя бы резонанс токов: реактивные мощности имеют разные знаки, что означает, что в момент, когда катушка отдает накопленную электромагнитную энергию, конденсатор ее накапливает и наоборот.
Уравнение переходного процесса вытекает из з-на Кирхгофа и Ома:
В начале конденсатор может быть заряжен до некоего напряжения, в катушке тоже может течь какой-то ток. Но интересен не конкретный процесс, а как в общем случае ведет себя свободная составляющая?
Для этого решим уравнение без правой части для напряжения конденсатора. Физически оно описывает процесс разрядки изначально заряженного конденсатора на резистор и катушку
Решение уравнения ищем в  р1 и р2 – корни характеристического
р1 и р2 – корни характеристического 
Корни могут быть разными! Действительными разными / совпадающими и комплексно- сопряженными

Когда корни комплексно-сопряженныеp1,2 = j
uсв A1 e t e j t A2 e t e j t
Примечательно, что еj t – это синусоида! Это видно, если разложить экспоненту как cos( t) + j sin( t). Т.е. мы видим сумму двух синусоид в разной фазе, причем амплитуда их меняется во времени (е t). Это как раз и есть периодический процесс обмена энергией между катушкой и конденсатором на резонансной частоте. Из общих понятий следует, что < 0 и зависит она от сопротивления: чем больше R, тем больше мощность выделяется на резисторе и тем быстрее запасенная конденсатором до начала переходного процесса энергия будет выведена из цепи в виде тепла.
Когда корни действительные разные числа
Мы имеем сумму экспонент с разными показателями.
Фактически, запасенная конденсатором энергия, выделяется в виде тепла за время, меньшее периода колебаний.
огда корни совпадают, мы получаем одну экспоненту. Рисовать не стал, сами изобразите.
Раздел 7. Магнитные цепи
Магнитные цепи – один из самых сложных разделов этого семестра и основа для понимания электрических машин. В нашем с вами случае дело осложняется тем, что требуется неплохое знание основ электромагнитных полей из физики. Записать с комментариями все, что я мог бы сказать на лекции нельзя. Поэтому обязательно читайте учебник, может быть, даже физики.
Я дам в лекции только самые-самые основы, фактически, комментарии к учебнику.
Магнитная цепь – это совокупность тел и областей пространства, где сосредоточено магнитное поле.
Магнитная цепь состоит из источников поля и прочих элементов (прочие элементы - ферромагнитные тела и воздушные зазоры).
В магнитной цепи не бывает приемников, подобных резисторам в электрических цепях, т.к. поле нельзя зачерпнуть и потребить. Но поле можно использовать в электромагнитных устройствах для превращения электрической энергии в механическую и обратно, т.к. поле – обязательное условие возникновения взамодействия, приводящего к полезной работе.
Несмотря на кажущуюся разницу между электрическими и магнитными цепями, в них больше общего, чем разного. Физика описывает все электромагнитные явления через систему уравнений Маквелла. Они определяют и электрические, и магнитные поля и явления. Поэтому электрические и магнитные цепи – суть разные стороны одной физической сущности, и не удивительно, что их описание будет схожим. Мы увидим, что существует прямая аналогия между электрическими и магнитными цепями и подходы к анализу магнитных цепей практически те же. Но, естественно, есть и своя специфика. Она в принципиальной нелинейности магнитных цепей, в разной цели анализа магнитных цепей по сравнению с электрическими цепями (в электрических важно найти ток и мощность устройств- двухполюсников, а в магнитных – обеспечить нужное поле в нужном месте, т.е. подобрать источник) и поэтому несколько разном подходе к анализу.

7.1. Основные характеристики и свойства магнитного поля
Основных характеристик магнитного поля три:
•Н (А/м) – напряженность магнитного поля.
•В (Тл) – магнитная индукция
•Ф (Вб) – магнитный поток
1. Напряженность магнитного поля Н |
|
Закон полного тока |
или |
|
Сумма произведений Н l вдоль любого замкнутого контура равна сумме токов, охваченных этим контуром. Здесь l – длина участка контура, Н- напряженность на этом участке.
Отсюда следует, что Напряженность магнитного поля Н характеризует источник магнитного поля – полный ток.
Важно: источником поля является ТОК! Даже в постоянном магните существуют спиновые токи, создающие поля доменов. Но на примитивном уровне можно считать постоянный магнит за источник магнитного поля.
Вторая формулировка уравнения характеризует поле в точке (первая содержит интеграл, а интеграл – всегда усреднение, в нашем случае по контуру). Ротор Н равен сумме векторов плотности тока. Ротор – оператор, показывающий форму поля. Если ротор равен нулю, поле незамкнуто (как поле электрического заряда), а если ротор не нулевой, это означает, что линии поля замкнуты! Если вы ткнули в точку, где тока нет, то в этой точке поле не замкнуто (это кусочек какой-то линии), а если попали в точку, где есть ток, то поле там замкнутое.
Т.е. закон полного тока выражает математически известную еще из школы картинку: металлические опилки, окружающие проводничок с током, группируются концентрическими окружностями вокруг проводника, а линии поля – концентрические окружности. Направление поля можно определить правилом правого винта или буравчика.
Главное: магнитное поле создается током, магнитное поле всегда замкнуто вокруг проводника с током.

2. Магнитная индукция В – силовая характеристика магнитного поля.
Силовая потому, что все силы зависят от индукции, а не от напряженности. Индукция зависит от напряженности (т.е. от источника поля – тока) и от магнитных свойств среды, в которой происходит взаимодействие.
Сила Лоренца Сила Ампера
Что физика говорит об индукции….
Дивергенция характеризует мощность источника поля (или его сток). Получается, что мощность источника поля всегда и везде равна нулю! Т.е. нет источника магнитной индукции, не существует точки, из которой исходили бы линии магнитного поля (или: не существует магнитных зарядов). Это естественно, раз линии поля Н замкнуты.
Вторая интегральная формулировка. Интеграл B ds (поток) через любую замкнутую поверхность равен нулю. Сколько линий поля вошло через замкнутую поверхность, столько же должно и выйти, раз поле замкнутое и не может выйти из точки или утечь в точку. (Кстати, аналогия с суммой токов в узле!)
3. Магнитный поток Ф
Индукция и напряженность характеризуют поле в точке. Но точечными характеристиками не удобно описывать целые устройства, т.к. поля распределены в пространстве. Поэтому используют поток, он дает представление о среднем поле внутри, например, сердечника трансформатора или электрической машины или катушки с током (кстати, индуктивность катушки L = Ф / I).
Закон электромагнитной индукции: если есть переменный магнитный поток через контур, на зажимах контура возникнет ЭДС.
(Эта ЭДС и есть причина появления напряжения на катушке индуктивности на переменном токе. Чем выше частота тока, тем больше при том же токе напряжение, что в цепях эквивалентно увеличению реактивного индуктивного сопротивления)
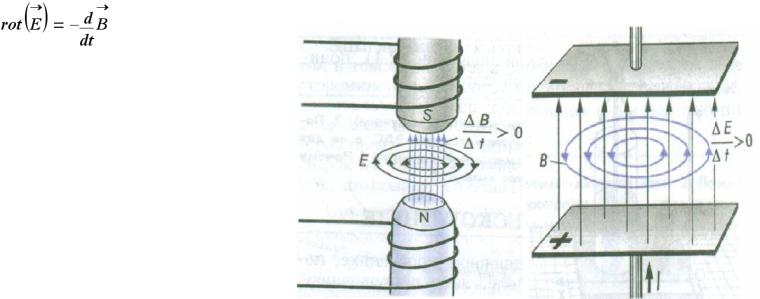
Или то же уравнение для точки |
Переменное электромагнитное |
Переменное электромагнитное |
|
поле между магнитопроводами |
поле между обкладками |
|
|
конденсатора |
Следствие: переменное магнитное поле порождает вихревое электрическое (справедливо и обратное утверждение), причем, поля В и Е перпендикулярны друг другу.
Если создать переменное магнитное поле в электропроводной среде, то вихревое поле Е (т.е. поле, линии которого замкнуты) создаст силу Кулона и электроны начнут двигаться по таким же замкнутым линиям, как и Е. Это вихревой ток (или ток Фуко), нагревающий все магнитопроводы, греющий кастрюли и сковородки на индукционной плите. Отчасти нечто похожее происходит и в микроволновках, хотя там эффект не только от электропроводности
Итоги напоминания о магнитном поле, которые мы будем использовать и не только в этом семестре:
1.Напряженность магнитного поля характеризует источник поля – электрический ток.
2.Магнитное поле зависит не только от напряженности, но и от магнитных свойств среды.
3.Силовой характеристикой магнитного поля является магнитная индукция: она определяет силу, действующую на движущиеся заряды (электрический ток) в магнитном поле.
4.Магнитное поле всегда замкнуто: нет источника или приемника магнитного поля.
5.Поток через замкнутую поверхность равен нулю.
6.Переменное магнитное поле порождает вихревое электрическое поле и, следовательно, электродвижущую силу (ЭДС), если в поле есть заряд.
7.Полная ЭДС в контуре, находящемся в переменном магнитном поле, определяется скоростью изменения магнитного потока через контур.

7.2. Магнитные характеристики вещества
Все вещества
Диамагнетики |
|
|
|
Парамагнетики |
|
Ферромагнетики |
|
||
|
|
|
|
|
|
|
|
|
|
В электротехнике применяются ферромагнетики. Диа и парамагнетики имеют проницаемость порядка 1, в то время как ферромагнетики – до сотен тысяч.
Основная характеристика ферромагнитного материала (ФММ) – зависимость В(Н), а не магнитная проницаемость!
Обычно приводят кривую намагничивания и предельную петлю гистерезиса
Кривая намагничивания

7.2. Магнитные характеристики вещества
Кривая намагничивания и петли гистерезиса объясняются структурой ферромагнетиков. ФММ состоят из доменов – микрообластей с единым магнитным полем (по сути, микроскопические постоянные магниты размером менее 1 мкм). Сразу после кристаллизации вещества домены расположены хаотично, поэтому в отсутствии внешнего поля (Н) индукция поля внутри ФММ В равна нулю.
Если приложить внешнее поле Н, то на домены- постоянные магниты начнет действоать сила, поворачивающая их вдоль внешнего поля. Из-за трения, не все домены повернутся, а только часть, но очевидно, что результирующее поле ФММ станет больше нуля и сложится с внешним полем, поэтому индукция вырастет не пропорционально полю Н.
Н=0, В=0
Если увеличивать внешнее поле Н, когда-нибудь (при Нmax) все домены
повернутся вдоль поля и прирост индукции за счет ФММ прекратится, достигается насыщение
При напряженностях выше напряженности Нmax рост индукции с ростом напряженности происходит пропорционально 0, как у немагнитных материалов.
Из-за кривизны кривой намагничивания оказывается, что нет какого-то единого значения . Проницаемость зависит от приложенного поля.
