Раздел 4. Линейные цепи периодического несинусоидального тока
Вводная часть
В общем случае периодические токи и напряжения могут быть несинусоидальными. Промышленная сеть использует синусоидальные токи, т.к. энергетически это наиболее выгодно: потери энергии при ее передаче и генерации меньше, чем при любой другой форме напряжения и тока.
Но в электронике несинусоидальные периодические токи и напряжения распространены. Причина появления несинусоидальности может быть разная: несовершенство источников синусоидального напряжения (в действительности создать точный синус очень сложно), импульсные помехи, нелинейные элементы в цепи синусоидального тока приводят к искажению формы сигналов, многие приборы в принципе работают на периодических несинусоидальных сигналах: цифровая электроника построена на импульсах прямоугольной формы, в аналоговых осциллографах, телевизорах с трубкой используются генераторы линейно-изменяющихся напряжений и т.п.
Наша задача на эту лекцию – познакомиться, как рассчитывать цепи несинусоидального тока и как для этого использовать уже известный аппарат цепей постоянного и переменного тока.
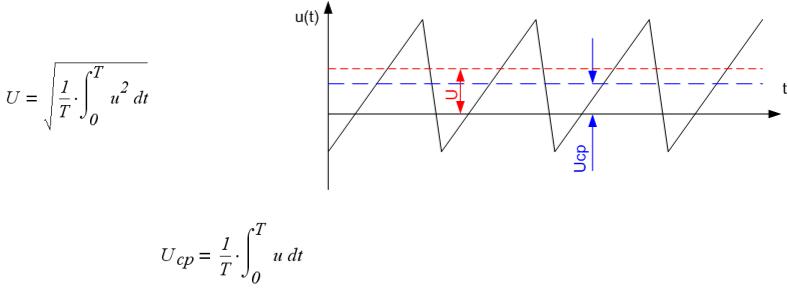
4.1. Способы представления и параметры несинусоидальных величин
Параметры несинусоидальных величин:
•Действующее значение
Характеризует работу электрического тока, как и в цепях синусоидального тока. Но в отличие от них, никакой связи с амплитудой нет.
•Среднее значение
•Период – минимальный интервал времени, через который все мгновенные значения повторяются.
Унесинусоидального тока нет таких характеристик как фаза или частота, т.к. эти характеристики присущи синусоидальному напряжению, а несинусоидальные ток – это, как мы скоро увидим, сумма синусоидальных токов разной частоты и амплитуды, ввести для них понятие одной частоты или фазы нельзя.
4.1. Способы представления и параметры несинусоидальных величин
Способы представления периодических несинусоидальных величин:
•Графическое изображение
•Разложение в ряд Фурье
•Спектральное представление
• Разложение в ряд Фурье
u(t) U0 u1 (t) u2 (t) u3 (t) ...
где : u1 (t) Um1 |
Sin( t 1 ); |
u2 (t) Um2 |
Sin(2 t 2 ); |
u3 (t) Um3 |
Sin(3 t 3 ) ... |
Несинусоидальная периодическая величина может быть представлена в виде суммы синусоид кратных частот разной амплитуды и фазы и постоянной составляющей U0. Каждую из
синусоид принято называть гармоникой. Ряд бесконечно длинный, в нем присутствуют гармоники с периодом T, 2Т, 3Т и до бесконечности.
Пример представления несинусоидальной функции в виде суммы гармоник
Есть исходное несинусоидальное периодическое напряжение. Мы математически разложили его в ряд Фурье и получили кучу
(бесконечно большую) гармоник кратных частот:
u(t) U0 u1 (t) u2 (t) u3 (t) ...
Очевидно, что у исходного напряжения нет постоянной составляющей, среднее значение у симметричного сигнала всегда равно нулю.
Если разложить в ряд представленное напряжение, гармоники будут с нулевой фазой: они все выходят из нуля, в общем случае это не так.
А теперь попробуем просуммировать по очереди гармоники
Сумма первых двух гармоник: Результат отдаленно напоминает форму
исходного напряжения.
Сумма первых трех гармоник: сходство с исходным сигналом уже больше
Сумма четырех гармоник дает уже хорошее приближение. Причем, если посмотреть на максимальное значение, то в последнем случае оно близко к максимуму исходного сигнала (5).
Чем больше гармоник, тем выше сходство. Гармоники бесконечной частоты позволяют описывать скачкообразные изменения сигнала и его
изломы.
Собственно представление в виде ряда Фурье и есть по сути единственный способ аналитически представить несинусоидальный сигнал, другое дело, что записывать бесконечные ряды как минимум долго, поэтому ряд Фурье представляют в виде спектра.
•Спектральное представление
Рисуют две картинки: зависимость амплитуды гармоник от их частоты (амплитудный спектр или амплитудно-частотная характеристика сигнала) и зависимость фазы гармоник от частоты (фазовый спектр или фазо-частотная характеристика сигнала).
u(t) U0 u1 (t) u2 (t) u3 (t) ...
где : u1 (t) Um1 |
Sin( t 1 ); |
u2 (t) Um2 |
Sin(2 t 2 ); |
u3 (t) Um3 |
Sin(3 t 3 ) ... |
В амплитудном спектре изображают амплитуды соответствующих гармоник и постоянную составляющую. Обычно с ростом номера гармоники ее амплитуда уменьшается.
Действующее значение можно рассчитать, зная действующие или амплитудные значения гармоник:
В фазовом спектре изображают фазы соответствующих гармоник. Номер гармоники никак не связан с фазой.
В спектрах указывают основные гармоники, обычно 3 – 5 штук. Связано это с тем, что работа тока связана с квадратом действующего значения, и 3-4 гармоники с наибольшими амплитудами «ответственны» за 90-95%
выделяемой в цепи мощности, а именно мощность в конце концов является целью расчетов цепей.
4.2. Анализ линейных цепей несинусоидального тока
Подход к анализу вытекает из способа представления несинусоидальных токов и напряжений. Т.к. несинусойда есть сумма синусоид, то источник несинусоидальной ЭДС можно заменить на несколько последовательно включенных источников ЭДС разной амплитуды, частоты и фазы. А такую цепь рассчитывают методом суперпозиции: ток от действия нескольких источников рассчитывается как сумма токов от действия каждого источника в отдельности.
Т.о. мы рассчитываем сначала цепь с источником постоянного напряжения, затем синусоидальные цепи на частоте = 2 / T, 2 , 3 , 4 и т.д. На каждой из гармоник цепь анализируется как обычная цепь синусоидального тока с использованием комплексных токов, напряжений, сопротивлений. На каждой частоте определяется мгновенное значение тока, которые затем и суммируются с учетом знака.
Алгоритм расчета:
1.Раскладываем периодическую ЭДС в ряд Фурье. Получаем цепь, в которой существует N синусоидальных ЭДС
e(t) E0 e1 (t) e2 (t) e3 (t) ...
где : e1 (t) Em1 Sin( t e1 );
e2 (t) Em2 Sin(2 t e2 );
e3 (t) Em3 Sin(3 t e3 ) ...
В соответствии с методом суперпозиции рассматриваем последовательно цепи с одним источником ЭДС и ищем ток.
Начинаем с расчета постоянной составляющей тока:
I0
В приведенном примере постоянный ток, очевидно не течет – не дает конденсатор. I0 = 0, все напряжение источника падает на конденсаторе.
Расчет на первой гармонике e1 (t) Em1 Sin( t e1 )
Представляем ЭДС первой гармоники в комплексном виде, рассчитываем комплексные сопротивления
i1 (t) Im1 Sin( t i1 )
Если требуется рассчитать мгновенные значения тока, тогда обязательно преобразовать вычисленный комплексный ток в выражение для мгновенного значения, потому что только в такой форме можно суммировать гармоники. Если нужно найти только действующее значение тока, можно не делать преобразований.
Расчет на N-й гармонике iN(t)
eN(t)
eN (t) EmN Sin(N t eN )
Представляем ЭДС N-й гармоники в комплексном виде, рассчитываем комплексные сопротивления
iN (t) ImN Sin(N t iN )
•Результирующий ток находим как сумму токов каждой гармоники
i(t) I0 i1 (t) i2 (t) i3 (t) ...
где : i1 (t) Im1 Sin( t i1 ); i2 (t) Im2 Sin(2 t i2 );
i3 (t) Im3 Sin(3 t i3 ) ... - токи, найденные нами при расчете цепей.
Если нужно найти только действующее значение (чтобы вычислить мощность), тогда:
|
|
1 T |
|
|
|
|
|
|
|
|
|
|
|
|
I |
2 |
dt |
2 |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
|
|
(i(t)) |
I0 |
Ik |
2 |
2 |
2 |
2 |
|
|||||
|
|
T 0 |
|
|
|
k |
I I0 |
I1 |
I2 |
I3 |
... |
|||
Здесь I – действующие значения токов на каждой из гармоник
Гармоник бесконечно много, но мощность трех-четырех основных составляет порядка 90-95% всей выделяемой мощности цепи, поэтому обычно ограничиваются расчетом цепи на 3-4 основных гармониках.
Метод суперпозиции, применяемый к цепям несинусоидального тока, можно использовать только в линейных цепях. Если цепь нелинейная, применяют математическое моделирование цепи. Там цепь рассчитывается с помощью законов Кирхгофа. Дифференциальные уравнения решаются итерационно численными методами.