
Лабы / Образец отчёта лабораторной работы №100
.pdf
Проверяем, что tПРИБ меньше случайной (ΔtСЛ) более чем в два раза. И тогда, в согласии с формулой
доверительную погрешность результата измерений приравниваем к
случайной t= |
tСЛ. |
|
|
|
|
|
|
Принимаем δ равным цене деления электронного секундомера: δ = |
|||||||
0.001 с. |
|
|
|
|
|
|
|
Тогда: |
tПРИБ |
1 |
k |
1 |
1.64 0.001 0.000547 с; |
||
3 |
|
3 |
|
||||
|
|
|
|
|
|
||

 0.0221 2 0.000547 2 0.0221.
0.0221 2 0.000547 2 0.0221.
2.8.Округлив погрешность и предварительный результат, записываем окончательный результат измерений:
t t t 2.87 0.02 с (с вероятностью p=0.90).
Задание 3. Оценка параметров закона распределения вероятностей с помощью гистограммы.
Из оставшихся значений находим максимальное и минимальное значения:
|
tmin 2.556 с, |
tmax |
3.120 с. |
|
|
|
|
||||
Теперь найдём ширину интервала: |
|
|
|
|
|
||||||
|
|
tmax tmin |
|
3.120 2.556 |
|
0.094 с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
6 |
|
|
6 |
|
|
|
|
|
|
|
Разбиение массива данных по ячейкам: |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
Номер |
Левая граница |
Правая граница |
ni |
|
ni |
|
|||||
интервала i |
|
интервала |
интервала = |
|
|
n |
|||||
|
|
|
|
|
= лев. гр. + δ |
|
|
|
|
||
|
|
|
|
|
|
|
|||||
1 |
2,556 |
|
|
2,650 |
1 |
0,0139 |
|||||
|
|
|
|
|
|
|
|||||
2 |
2,650 |
|
|
2,744 |
9 |
0,1250 |
|||||
|
|
|
|
|
|
|
|||||
3 |
2,744 |
|
|
2,838 |
20 |
0,2778 |
|||||
|
|
|
|
|
|
|
|||||
4 |
2,838 |
|
|
2,932 |
21 |
0,2917 |
|||||
|
|
|
|
|
|
|
|||||
5 |
2,932 |
|
|
3,026 |
15 |
0,2083 |
|||||
|
|
|
|
|
|
|
|||||
6 |
3,026 |
|
|
3,120 |
6 |
0,0833 |
|||||
|
|
|
|
|
|
|
|
|
|||
Примеры расчётов к таблице: |
|
|
|
|
|
|
|
||||
2.556 + 0.094 = 2.650, |
|
2.650 + 0.094 = 2.744, |
|
|
|
||||||
2.744 + 0.094 = 2.838, |
|
2.838 + 0.094 = 2.932, |
|
|
|
||||||
11
|
|
2.932 + 0.094 = 3.026, |
|
|
3.026 + 0.094 = 3.120; |
|
|||||||
n1 |
|
1 |
0.0139 |
, |
n2 |
|
9 |
0.1250 , |
n3 |
|
20 |
0.2778 , |
|
n |
|
72 |
|
|
n |
|
72 |
|
n |
|
72 |
|
|
n4 |
|
21 |
0.2917 |
, |
n5 |
|
15 |
0.2083 , |
n6 |
|
6 |
0.0833 . |
|
n |
|
72 |
|
|
n |
|
72 |
|
n |
|
72 |
|
|
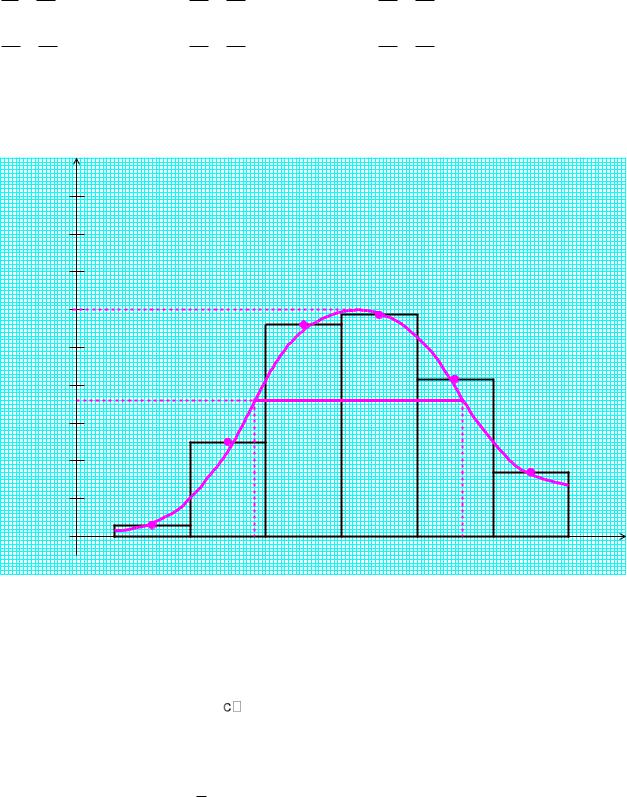
Строим гистограмму экспериментальных значений и кривую закона |
|||||||||||||
распределения: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
ni/n |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.20 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
t, c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.556 |
2.650 |
|
|
2.744 |
2.838 |
2.932 |
3.026 |
3.120 |
||
На уровне 0.6 от максимального значения:
0.6 0.30 0.18 , –
находим ширину кривой закона распределения:
2 2.99 2.73 0.26 |
|
0.26 |
0.13 |
с. |
|
2 |
|||||
|
|
|
|
Ответ: 1) Секундная стрелка пройдёт 3 деления за промежуток, заключённый в следующем интервале (2.87–0.02; 2.87+0.02) секунд (с вероятностью p=0.90): t t t 2.87 0.02 ;
2)S(ti) = 0.113 с;
3)σ = 0.13 с.
12
Вывод: в результате проделанной работы получены практические навыки в освоении алгоритма обработки результатов прямых многократных прямых измерений, построена гистограммы экспериментальных значений определяемой величины и произведена оценка параметров распределения Гаусса из кривой закона распределения.
13
