1.2 Порядок работы в программе «Площадка»

Рассмотрим дальнейшее на примере: Пусть есть площадка120*160м., расположенная на картограмме (приложение 2) между осями по вертикали – 4-8, по горизонтали – p3-p6. Сторона квадрата – 40 м.

Запустить программу «Площадка»:

Откроется окно «предупреждение о безопасности» -если есть окно - макросы не отключать; если нет – зайти в Сервис/Макрос/Безопасность/ поставить отметку Средняя/ок – выйти из программы и снова запустить.

1)Зарегистрироваться:

2)Выбрать способ ввода данных и далее: Для нашего случая - выбираем « 2. По заданным осям». 3) В появившемся окне:

вводим номера осей.

4)Ставим точку «с уклоном». Затем нажимаем клавишу «Построение площадки». После этого компьютер попросит выбрать направление уклонов. Нужно выбрать направление водостока, которое диктуется местностью.

Ставим точку в выбранном направлении уклонов и нажимаем клавишу «Продолжить».

5) В этом окне нажимаем в командной строке «Надстройки»,

6) и окно приобретает вид:

7)Теперь нажимаем: «Проектные отметки», компьютер находит проектные (красные отметки).

8)После нажатия кнопки «Рабочие отметки» появляется страница:

Здесь представлена площадка с рабочими отметками и предлагается перейти к подсчету объемов земляных работ на площадке.

9) Для этого нужно нажать «вычисление объемов квадратов».

Появилась такая таблица объемов:

Далее, для уменьшения в последующих расчетах трудоемкости решения задачи распределения земляных масс, следует зайти в лист объемы и сгруппировать объемы квадратов и их элементов (одного знака) в массивы, относя каждый элемент объема к какому-либо массиву (присвоить номера каждому массиву). Номера массивам присваиваются отдельно для выемки и насыпи ( в обоих случаях – начиная с 1). Вначале это желательно сделать на плане площадки. Потом проставить номера массивов в таблице объемов (столбцы 19 и 20).

10) По команде «вычисление объемов массивов» компьютер строит площадку с указанием центров тяжести каждого массива

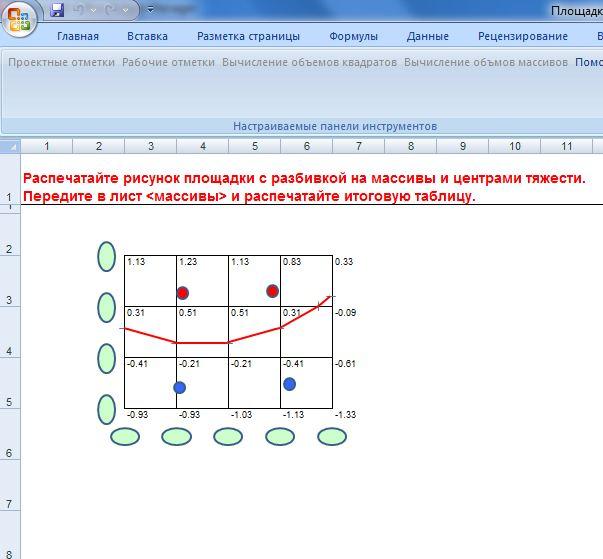
и в листе «массивы» - итоговую таблицу: «Таблица расстояний между массивами».

На этом заканчивается решение задачи с помощью программы «Площадка».

После определения объемов массивов выемок и насыпей надо решить: откуда, куда транспортируется грунт, какими машинами целесообразно разрабатывать грунт, какими машинами грунт доставляется к месту укладки. Ответы на эти вопросы мы называем распределением земляных масс. Конечно, хочется ответить на эти вопросы наилучшим способом. Задача распределения земляных масс многовариантна, поэтому необ­ходимо найти наиболее выгодный, оптимальный вариант.

1.3 Сущность и возможности задачи линейного программирования

Для решения этой задачи применена так называемая транспортная задача, или задача о назначениях, являющаяся частным случаем линейного программирования, которая позволяет найти оптимальное решение – наилучшее по какому-то критерию. В качестве критерия оптимальности могут быть выбраны: минимальная стоимость варианта, минимальный срок производства работ, наименьшие энергозатраты и пр.

Массивы выемок, где нужно разрабатывать грунт будем называть поставщиками. Соответственно массивы насыпей – потребителями. Пусть имеется m поставщиков и n потребителей грунта. Считаем, что качество товара (грунта) у поставщиков одинаковое и этот товар (грунт) пригоден для всех потребителей. Пусть c_ij – удельные затраты на разработку и доставку грунта от i-го поставщика к j-му потребителю. Удельные затраты зависят от выбранного критерия оптимальности варианта распределения. Если, к примеру, выбран критерий минимальной стоимости, то

c_ij - себестоимость разработки и перемещения одного кубометра грунта от поставщика i к потребителю j.

Если выбран критерий минимальной продолжительности производства работ, то

c_ij – величина, обратная суточной производительности комплекта машин, разрабатывающих и перемещающих грунт от поставщика i к потребителю j.

В курсовом проекте будем находить вариант с минимальной стоимостью.

Обозначим через v_ij объемы поставок грунта от i-го поставщика к j-му потребителю.

Название транспортной рассматриваемая задача получила потому, что к ней сводится оптимизация плана перевозок грузов из m пунктов отправления с запасами а₁,..., а_m в n пунктов назначения с потребностями b₁,…b_n Роль коэффициентов с_ij в целевой функции играют удельные стоимости, т.е. себестоимости разработки и перевозки одной единицы груза из пункта i в пункт j.

Переменные в этой задаче снабжены индексами i, j. Если первый индекс принимает m значений, а второй - n, то общее число перемен­ных (размерность задачи) равно, очевидно, mn. Сущность задачи состоит в минимизации функции:

, (11)

Обычно предполагается дополнительное соблюдение равенства

, (12)

Сумма объемов поставщиков равна сумме объемов потребителей - иначе задача не будет иметь решений.

При этих условиях имеется решение сформулированной задачи минимизации, содержащее не более (m+ n – 1) ненулевых значений перемен­ных. Эти переменные – объемы поставок от i- того поставщика к j-тому потребителю - мы будем называть назначениями.

При решении транспортной задачи пользуются двумя тп матрицами -матрицей планов Р и матрицей удельных стоимостей С, подвергая их специальным преобразованиям.

Построение матрицы стоимостей.

В матрице стоимостей могут быть реальные себестоимости разработки и перевозки 1 м³ грунта от поставщика i к потребителю j -c_ij. Если поставка невозможна(например, грунт непригоден для данного потребителя, поставка обозначается, как «запрещенная» - ЗП. И если для математического решения (обязательность вывоза всех поставщиков и обязательность заполнения всех потребителей) нужно, предположим, перемещать грунт из карьера в отвал, такая поставка обозначается, как «фиктивная поставка» - ФП.

Реальные себестоимости разработки и перевозки 1 м3 грунта от поставщика i к потребителю j -c_ij находим их по графикам единичной себестоимости, в зависимости от дальности перемещения грунта (прил.3). Методика работы с графиками единичной себестоимости проста. Смотрим, на какое расстояние (ось «х») перевозится грунт и поднимаем перпендикуляр до пересечения с первой линией графика и смотрим в сноске, какой комплект машин целесообразно применить на этом участке, затем проводим от линии перпендикуляр к оси «y» и определяем себестоимость разработки и перевозки руб./м³ грунта на этом участке.

В клетках матрицы, где обозначена запрещенная поставка – ЗП – записываем заведомо большую цену – например 1000 руб./м³.

В клетках матрицы, где обозначена фиктивная поставка – ФП – записываем себестоимость разработки и перевозки грунта – 0 руб./м³.

Для формирования матрицы планов Р на начальном шаге делается ровно т + п - 1 назначений (некоторые из них могут быть нулевыми) с тем, чтобы, полностью удовлетворить спрос всех потребителей грунта, и в то же время вывезти все поставщики.

Вернемся к рассматриваемому примеру.

Для решения задачи распределения земляных масс массивов грунта на площадке с использованием транспортной задачи линейного программирования воспользуемся разработанной на кафедре «Управление и технология строительства» компьютерной программой «NewTZ».

С тем, чтобы уравнять объемы поставщиков и потребителей введем поставщик-карьер, расположенный рядом с площадкой – где наибольшие рабочие отметки выемок. Таким образом увеличиваем объем поставщиков за счет увеличения площади площадки. (Добавился массив №3) Этот объем желательно наметить заведомо большим: скажем равный объему всех потребителей. Точно так же поступаем с потребителями, намечая большой отвал рядом с площадкой, где самые большие рабочие отметки насыпей:

3 карьер