
- •Институт холода и биотехнологий
- •Институт холода и биотехнологий
- •© Афанасьева н.А., Новотельнова а.В., Ерофеева и.А., 2012 задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Справочные данные по диодам (фрагмент каталога)
- •Задача 7
- •Справочные данные по асинхронным двигателям (фрагмент каталога)
- •Передаточные числа зубчатых цилиндрических и конических передач (по гост 2185-66, гост 12289-56) и двухступенчатых редукторов (по гост 2185-66)
- •Задача 8
- •Список литературы
- •Содержание
- •Институт холода и биотехнологий
- •Батяев Анатолий Алексеевич
- •Ерофеева Ирина Александровна
- •Электротехника и электроника
- •Примеры расчета контрольных заданий
Передаточные числа зубчатых цилиндрических и конических передач (по гост 2185-66, гост 12289-56) и двухступенчатых редукторов (по гост 2185-66)
|
1,0 |
1,06 |
1,12 |
1,18 |
1,25 |
1,32 |
1,40 |
1,50 |
1,60 |
1,70 |
1,80 |
1,90 |
|
2,0 |
2,12 |
2,24 |
2,36 |
2,5 |
2,65 |
2,8 |
3,0 |
3,15 |
3,35 |
3,55 |
3,75 |
|
4,0 |
4,25 |
4,5 |
4,75 |
5,0 |
5,3 |
5,6 |
6,0 |
6,3 |
6,7 |
7,1 |
7,5 |
|
8,0 |
8,5 |
9,0 |
9,5 |
10,0 |
10,6 |
11,2 |
11,8 |
12,5 |
14,0 |
16,0 |
18,0 |
|
20,0 |
22,4 |
25,0 |
28 |
31,5 |
35,5 |
40 |
45 |
50 |
56 |
63 |
71 |
Задача 8
Задача посвящена вопросу снижения уровня реактивной мощности в электрических сетях (повышение коэффициента мощности – cos φ).
Реактивная мощность, потребляемая асинхронным двигателем (АД) при степени загрузки Кнг, определяется зависимостью
Qад
= Qx.x
+ (Qн – Qx.x
) K![]() ,
,
где Qx.x – реактивная мощность холостого хода АД равная
Qx.x
=
![]() ,
,
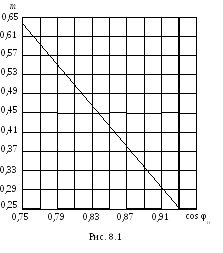
где m – расчетный коэффициент, зависящий от номинального коэффициента мощности сos φн (рис. 8.1); Qн – реактивная мощность АД при номинальной нагрузке
Qн
=
![]() .
.
Суммарная реактивная мощность, подлежащая компенсации при работе двух АД,
Qк
=
![]() +
+
![]() .
.
Величина емкости С, мкФ батареи конденсаторов, включаемых в одну фазу, при условии соединения их в треугольник равна:
C
=
![]() ,
,
так как реактивная (емкостная) мощность одной фазы вычисляется по формуле (подобно однофазному переменному току)
Qc
=
![]() bc
= =
bc
= =
![]() 2fC
=
2fC
=
![]() 314С.
314С.
Поскольку
в условии задачи требуется подсчитать
величину емкости батареи конденсаторов,
включенных в одну фазу, при условии
полной компенсации реактивной
мощности (Qк) при работе двух
двигателей, подключенных к сети
трехфазного тока (Qсф
=
![]() ),
окончательная расчетная формула
имеет вид: C
=
),
окончательная расчетная формула
имеет вид: C
=
![]()
Пример. Исходные данные представлены в табл. 8.1.
Таблица 8.1
|
Uд, B |
Pн1, кВт |
Кнг1 |
сos φн1 |
н1 |
Pн2, кВт |
Кнг2 |
сos φн2 |
н2 |
|
380 |
18,5 |
0,6 |
0,88 |
0,9 |
30 |
0,8 |
0,89 |
0,91 |
Решение
1. Определяем номинальную реактивную мощность, потребляемую АД1
Qн
=
![]() =
=
![]() = 11,1 квар.
= 11,1 квар.
2. Определяем реактивную мощность АД1 при коэффициенте нагрузки Кнг1 = 0,6
Q0,6
= Qx.x1
+ (Qн1 – Qx.x1)
К![]() ,
,
где
Qх.х1 =
![]() =
=
![]() = 7,19 квар; m = 0,35 –
находится из графика (рис. 8.1).
= 7,19 квар; m = 0,35 –
находится из графика (рис. 8.1).
QАД1
= Q0,6 = Qx.x1
+ (Qн1 –
Qx.x1)
К![]() =
=
= 7,19 + (11,1 – 7,19) 0,62 = 8,6 квар.
3. Определяем номинальную реактивную мощность потребляемую АД2
Qн1
=
![]() = (30/0,91) 0,51 = 16,89 квар.
= (30/0,91) 0,51 = 16,89 квар.
4. Определяем реактивную мощность АД2 при коэффициенте нагрузки Кнг2 = 0,8 (см. график рис. 8.1)
QАД2
= Qx.x2
+ (Qн2 –
Qx.x2
) К![]() ,
,
где Qх.х2
=
![]() =
= 30/0,91 0,35 = 11,54;
=
= 30/0,91 0,35 = 11,54;
QАД2 = Q0,8 = 11,54+(16,89 – 11,54) 0,64 = 14,96 квар
5. Определяем общую реактивную мощность, подлежащую компенсации,
Qк = QАД1 + QАД2 = 8,6 + 14,96 = 23,56 квар
6. Определяем величину емкости батареи конденсаторов, включенных в одну фазу при Uл = 380 В
сф =
![]() = 23,56∙ 106 / 942
3802 =173 мкФ.
= 23,56∙ 106 / 942
3802 =173 мкФ.
7![]() .
Определяем реальную активную мощность
двух АД
.
Определяем реальную активную мощность
двух АД
Р =
![]()
![]() +
+![]()
![]() =
(18,5/0,9) 0,6 + (30/0,91) 0,8 =
=
(18,5/0,9) 0,6 + (30/0,91) 0,8 =
= 12,33 + 26,37 = 38,7 кВт.
