Потери напора по длине

Напомним, что потери напора по длине мы будем определять только в случае равномерного движения жидкости в прямолинейном трубопроводе, т. е. когда средняя скорость потока не изменяется по величине и по направлению.

Анализ уравнения Бернулли не дает нам ответа на вопрос, как влияют физические свойства жидкости и геометрические размеры трубопровода на величину потерь напора. Это следует из самого уравнения, если преобразовать его к следующему виду:

. (2.71)

Как видно из уравнения (2.71), величину потерь напора определяет лишь движущая сила потока жидкости. Однако и жидкости по своим физическим свойствам отличаются друг от друга, и трубопроводы могут иметь разные формы поперечного сечения, различные диаметры и длину. Частичные ответы на поставленные вопросы дает основное уравнение равномерного движения жидкости.

Основное уравнение движения жидкости в трубопроводе круглого поперечного сечения

Рассмотрим напорное равномерное движение в наклонном трубопроводе, который имеет круглую форму поперечного сечения по всей своей длине. Пусть рассматриваемый трубопровод имеет диаметр d и площадь поперечного сечения S. Очевидно, что величина смоченного периметра для данного трубопровода будет вполне конкретной и равна П. Допустим, что трубопровод расположен под углом α к горизонтальной поверхности (плоскости отсчета 0–0), как это показано на рис. 2.19.

Рис. 2.19. Расчетная схема к выводу основного уравнения

равномерного движения

Выделим в потоке сечениями I–I и II–II объем жидкости длиной L. Рассмотрим силы, определяющие равномерное движение выделенного объема жидкости.

Из категории поверхностных сил на рассматриваемый объем будут действовать силы давления окружающей жидкости на торцы цилиндра слева F₁ и справа F₂, а также силы внутреннего трения Т жидкости о твердую стенку трубопровода.

Из категории массовых сил, действующих внутри рассматриваемого объема, следует выделить лишь силу тяжести G. Так как движение жидкости равномерное, т. е. средняя скорость потока постоянна во времени, силы инерции в данном случае не проявляются (ускорение равно нулю).

Силы давления определяем обычным путем, как произведение величины давления на площадь действия этого давления, т. е.

и

Силу трения жидкости о стенку трубопровода Т можно найти из определения касательных напряжений (см. уравнение (1.9) [1]):

(2.72)

где τ – касательное напряжение, возникающее в результате трения жидкости о стенку трубопровода, Н/м²; П – смоченный периметр, м; L – длина рассматриваемого объема, м.

Произведение смоченного периметра П на длину рассматриваемого объема L дает величину площади поверхности трения жидкости о твердую стенку трубопровода.

Массовая сила – сила тяжести может быть определена как произведение массы на ее ускорение. Так как поток жидкости рассматривается в условиях гравитационного поля Земли, то величина ускорения известна и равна g. Величину массы жидкости m в рассматриваемом объеме V можно представить как произведение плотности жидкости ρ на величину этого объема, т. е.

Так как форма объема вполне определенна и является цилиндрической, то окончательно уравнение для расчета силы G будет иметь следующий вид:

(2.73)

Составим уравнение равновесия сил, действующих на выделенный объем и внутри него в направлении движения жидкости, т. е. спроецируем все рассмотренные выше силы на ось x, совпадающей с осью трубопровода:

(2.74)

где G_x – проекция силы тяжести на ось x, .

Из рис. 2.19 следует, что углы α и β равны как соответствующие углы треугольников со взаимно перпендикулярными сторонами. Тогда можно записать, что

Подставляя найденные значения сил в уравнение (2.74), получим

. (2.75)

Разделив обе части уравнения (2.75) на и выполнив перегруппировку слагаемых, получим

. (2.76)

Левая часть уравнения (2.76) есть не что иное, как потери напора по длине h_дл; в правой части уравнения отношение , где R – гидравлический радиус.

Отсюда следует, что

. (2.77)

Преобразуем уравнение (2.77), разделив левую и правую его части на L. В результате имеем

(2.78)

Откуда

, (2.79)

где i – гидравлический уклон.

Уравнение (2.79) получило название «основное уравнение равномерного движения». Оно показывает, что потери напора по длине в первую очередь зависят от вязкости жидкости. Численно это влияние определяется через коэффициент динамической вязкости, входящий в уравнение (1.9) [1].

Величины касательных напряжений неодинаковы по сечению потока жидкости.

Проанализируем уравнение (2.79), выразив гидравлический радиус через геометрический радиус трубы. Ранее было показано, что эти два параметра для напорного движения жидкости в трубопроводе круглого сечения связаны между собой следующим соотношением:

Очевидно, что на оси потока r = 0, а на стенке трубопровода r = r₀. Тогда в соответствии с уравнением (2.79) на оси потока будем иметь τ = 0, а на стенке трубы – τ = τ_ст. Уравнение (2.79) носит линейный характер, поэтому для построения эпюры касательных напряжений достаточно этих двух точек (рис. 2.20).

а

б

u

τ

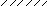
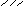
Рис. 2.20. Эпюры:

а – касательных напряжений;

б – локальных скоростей в поперечном сечении трубопровода

На рис. 2.20 также показана эпюра локальных скоростей для данного сечения потока. Как видно из рисунка, полученная нами теоретически эпюра касательных напряжений в целом правильно отражает наблюдаемую в реальности картину движения частиц жидкости. Максимальные касательные напряжения возникают на стенке трубопровода, что приводит к уменьшению скорости частиц жидкости до нуля.

На оси потока влияние твердых неподвижных стенок сводится к минимуму для данного диаметра трубы, а локальная скорость частиц жидкости становится максимальной в данном сечении, т. е. u = u_max. Эти выводы получили многочисленные экспериментальные подтверждения. Учитывая, что максимальные касательные напряжения возникают на стенке трубопровода, практический интерес представляет возможность их измерения. Посмотрим, как это можно сделать. Для этого вернемся к уравнению (2.79) и раскроем понятие гидравлического уклона. Для горизонтально расположенного трубопровода постоянного диаметра

(2.80)

подставляя зависимость (2.80) в уравнение (2.79), записанное для касательных напряжений на стенке, получим

(2.81)

Учитывая, что выражение есть разность пьезометрических высот, каждая из которых может быть легко измерена путем размещения в данных сечениях пьезометров, определение τ_ст не представляет сложности.

Отсюда следует:

– касательные напряжения на стенке трубопровода можно легко определить экспериментально, измерив перепад давления;

– касательные напряжения зависят от геометрических размеров трубопровода, а именно от длины и диаметра;

– касательные напряжения зависят от рода жидкости, точнее, от ее физических свойств – вязкости и плотности.

Однако, как показали многочисленные эксперименты по изучению равномерного движения, этих данных недостаточно для проведения надежных теоретических расчетов потерь напора по длине.