ЛР№2ИО

ФГБОУ ВО

«Уфимский государственный авиационный технический университет»

Кафедра АСУ

Отчет по лабораторной работе №2

«РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИОРВАНИЯ»

Выполнил: студент группы ИВТ-414

Балыбердин Н.А.

Проверила:

преподаватель каф. АСУ

Кондратьева О.В.

УФА-2020

Цель работы:

• Построение математической модели задачи линейного программирования;

• Решение задачи линейного программирования графическим методом;

Для изготовления двух видов продукции используется три вида сырья. При производстве единицы продукции первого вида затрачивается 13 кг сырья первого вида, 4 кг сырья второго вида и 3 кг сырья третьего вида. При производстве единицы продукции второго вида затрачивается 2 кг сырья первого вида, 4 кг сырья второго вида и 14 кг сырья третьего вида. Запасы сырья первого вида составляют 260 кг, второго –124 кг, третьего –280 кг. Прибыль от реализации единицы продукции первого вида составляет12 ден. ед., прибыль от реализации единицы продукции второго вида составляет 10 ден. ед. Максимизировать прибыль от реализации продукции.

Составим таблицу содержащую наши данные:

Сырьё	1 вид	2 вид	3 вид	Прибыль
Продукция А	13 кг	4 кг	3 кг	12 ден.ед.
Продукция В	2 кг	4 кг	14 кг	10 ден.ед.
Запасы	260 кг	124 кг	280 кг

Составим математическую модель.

х – продукция А, у – продукция В.

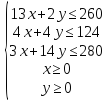
Целевая функция: F(x,y) = 12*x+10*y → max

Решим графическим методом данную систему.

Превратим неравенство в равенство.

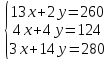
Решим уравнения.

1 уравнение: х = 0, у = 130 или х = 20, у = 0;

Получим точки: (0;130) и (20;0)

2 уравнение: х = 0, у = 31 или х = 31, у = 0;

Получим точки: (0;31) и (31;0)

3 уравнение: х = 0, у = 20 или х = 70, у = 0;

Получим точки: (0;20) и (70;0)

По этим точкам строим график:

Теперь покажем на графике ОДЗ и целевую функцию (градиент).

ОДЗ - Многоугольник - ABCDO

Найдём оптимальную точку.

B - Точка пересечения прямых:

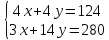
Решим эту систему и получим координаты точки B: x = 14, y = 17 (14;17)

Найдем функцию в этой точке. F (14;17) = 338 ден.ед.

C – Точка пересечения прямых:

Решим эту систему и получим координаты точки C: х = 18, у = 13 (18;13)

Найдем функцию в этой точке. F (18;13) = 346 ден.ед.

Так как F(B) < F(C). Оптимальная точка - C.

Итак, необходимо произвести продукцию А = 18, а продукцию В = 13 при этом прибыль будет максимальной и будет равна 346 ден.ед.

Вывод: Научились строить математические модели и решать их с помощью графического метода.