МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра математического обеспечения и применения ЭВМ

отчет

по практической работе №11

по дисциплине «Вычислительная математика»

Тема: Решение системы линейных уравнений

Студент гр. 8383		Ларин А.
Преподаватель		Сучков А.И.

Санкт-Петербург

2019

Цель работы.

Исследование и реализация различных методов решения систем линейных алгебраических уравнений.

Основные теоретические положения.

Методы решения систем линейных алгебраических уравнений (СЛАУ) делятся на две группы. К первой группе принадлежат так называемые точные, или прямые, методы – алгоритмы, позволяющие получить решение системы за конечное число арифметических действий. Сюда относятся известное правило Крамера нахождения решения с помощью определителей, метод Гаусса (метод исключений) и метод прогонки. Правило Крамера при реализации на ЭВМ не применяется ввиду значительно большего по сравнению с методом Гаусса числа арифметических действий. Метод Гаусса используется при решении систем до порядка 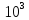. Метод прогонки применяется для решения важного класса специальных систем линейных уравнений с трехдиагональной матрицей, часто возникающей в практических приложениях.

Решение систем линейных алгебраических уравнений методом Гаусса

Рассматривается СЛАУ 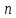-го порядка

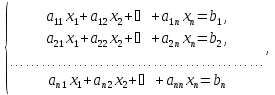
что в векторном виде записывается как .

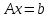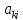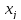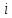Суть метода исключения по главным элементам (метод Гаусса) заключается в следующем. Находится наибольший по абсолютной величине коэффициент . Для исключения из -го уравнения 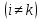необходимо умножить 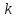-е уравнение на 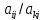и вычесть его из 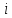-го уравнения, после чего процесс повторяется для исключения другого неизвестного из оставшихся 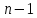уравнений и т.д. В результате система уравнений приводится к треугольному виду

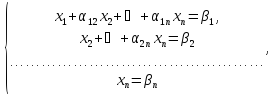
из которого легко находятся неизвестные 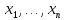. Процесс приведения системы к треугольному виду называется прямым ходом, а нахождение неизвестных 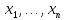– обратным ходом метода Гаусса.

Следует отметить, что если матрица заданной системы вырожденная, то перед исключением некоторой неизвестной главный элемент 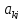окажется равным нулю, что и будет свидетельствовать о равенстве нулю определителя системы. Мерой обусловленности матрицы 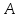называют величину 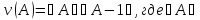– норма матрицы 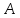. Мера обусловленности равна максимально возможному коэффициенту усиления относительной погрешности от правой части к решению СЛАУ. Если матрица 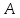симметричная и выбрана вторая норма, то мера обусловленности может быть найдена как 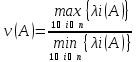где 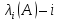-е собственное число матрицы 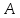. Если 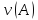большая, то матрица 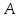называется плохо обусловленной, в противном случае – хорошо обусловленной.

Решение систем линейных алгебраических уравнений методом простой итерации. Рассматривается система уравнений вида 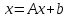, где 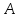– заданная числовая квадратная матрица 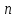-го порядка, а 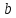– заданный вектор (свободный член). Метод простой итерации состоит в следующем. Выбирается произвольный вектор x (начальное приближение), и строится итерационная последовательность векторов по формуле

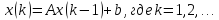
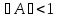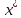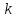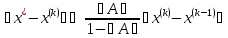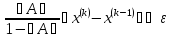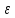Доказана теорема, что если норма , то система уравнений имеет единственное решение и итерации сходятся к решению со скоростью геометрической прогрессии. Для оценки погрешности -го приближения широко применяется неравенство , которое может быть использовано для принятия решения об останове итерационного процесса при выполнении условия , где – некоторая заданная погрешность вычислений.