Дифференциальное уравнение теплопроводности

В ыделим в теле элементарный параллелепипед с ребрами dx, dy, dz. Если через этот параллелепипед тепло распространяется теплопроводностью, то за промежуток времени dτ в него входят количества тепла Q_x, Q_y, Q_z, через противоположные грани – выходят количества тепла соответственно Q_{x + dx} ,Q_{y + dy}, Q_{z + dz}.

Разность между количеством тепла, введенным в параллелепипед за dτ и выведенным из него за тот же промежуток времени определяется равенством:

.

Согласно закону Фурье:

, (17.0)

,

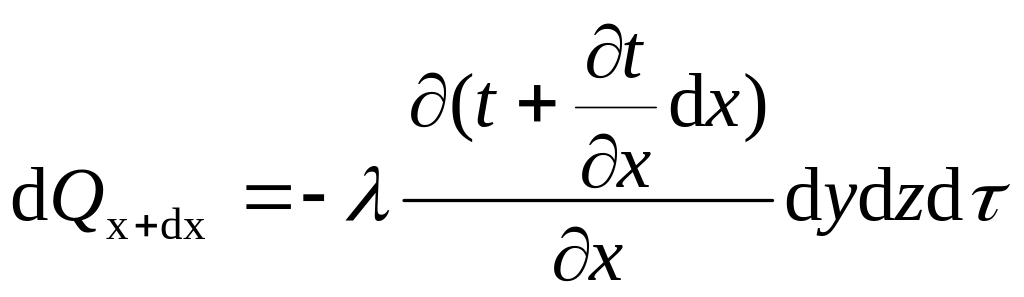, тогда

.

Аналогично получаем:

.

Общее приращение теплоты составит:

.

На основе закона сохранения энергии это приращение тепла пойдет на изменение энтальпии параллелепипеда за время Δτ.

,

где с – теплоемкость вещества, ρ – плотность.

Если приравнять эти величины, то

.

Если выражение – коэффициент температуропроводности, обозначить a, то выражение можно переписать:

Уравнение теплопроводности плоской стенки

При установившемся процессе , то, поскольку коэффициент не может равняться нулю, следовательно, . (17.1)

Это уравнение называют уравнением теплопроводности плоской стенки в неподвижной среде при установившемся тепловом режиме.

Рассмотрим перенос теплоты теплопроводностью при установившемся процессе через плоскую стенку, длина и ширина которой существенно больше ее толщины.

Примем, что t _ст1 > t _ст2, температурное поле одномерно и, следовательно, температура изменяется только по одному направлению – вдоль оси х. Поэтому:

, следовательно, в данном случае уравнение (17.1) имеет вид:

. (17.2)

Интегрирование этого уравнения (17.2) приводит к функциям:

и . (17.3)

Для определения значений С₁ и С₂ примем граничные условия:

при х = 0 t = t_ст1 и, поэтому, t_ст1= С₂,

при х = δ t = t_ст2 и, поэтому, t_ст2 = С₁∙δ +С₂ ; t_ст2 = С₁∙δ+ t_ст1.

Откуда .

Подставив значения констант С₁ и С₂ уравнение (17.3), находим

.

Тогда

.

Полученное значение температурного градиента подставим в закон Фурье (17.0):

или

. (17.4)

Это уравнение называют уравнением теплопроводности плоской стенки. Запишем его через плотность теплового потока:

.

Коэффициент характеризует тепловую проводимость стенки, – термическое сопротивление.

Для многослойной стенки:

, .

.

.

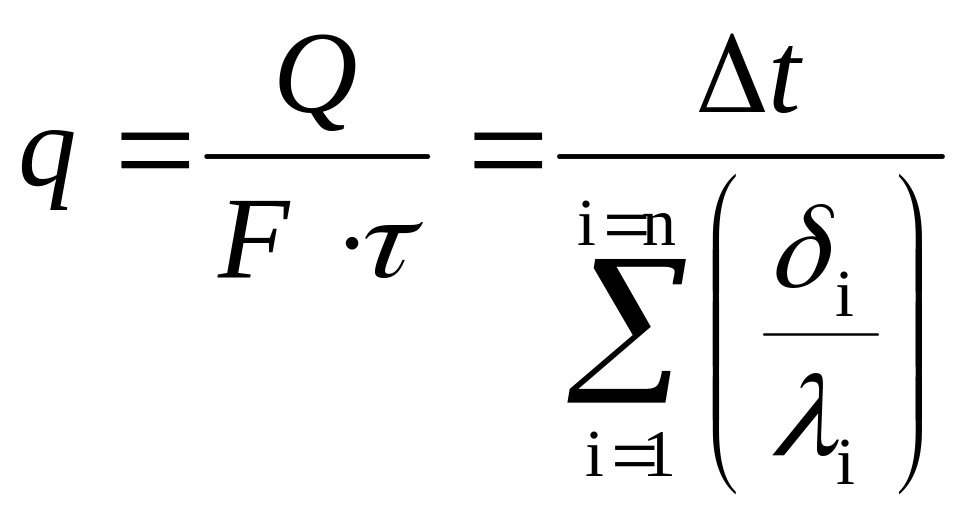Из этого выражения можно получить:

.

Уравнение теплопроводности цилиндрической стенки

Перепишем уравнение Фурье (17.0) в полярных координатах.

. (17.5)

Боковая поверхность цилиндра радиуса r равна: , где L – длина цилиндрической стенки. Перепишем (17.5):

.

Разделяем переменные:

.

Интегрируем это уравнение в пределах от r₁ до r₂ и соответственно – от до :

,

откуда

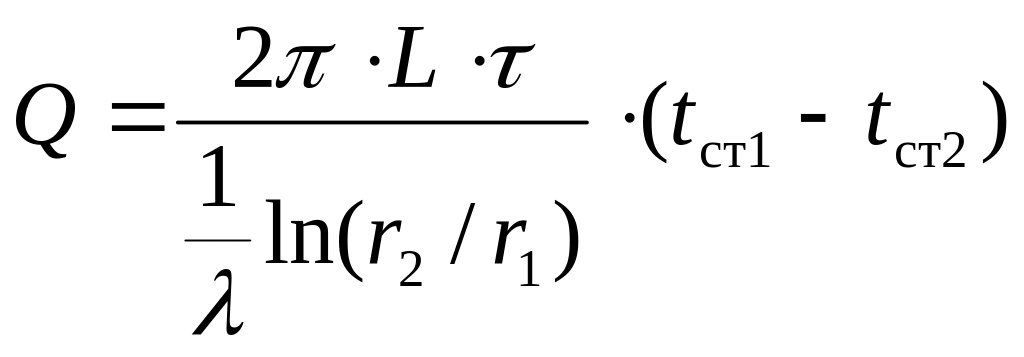. (17.6)

Уравнение (17.6) показывает, что по толщине цилиндрической стенки температуры изменяются по криволинейному (логарифмическому) закону. Это уравнение представляет собой уравнение теплопроводности цилиндрической стенки при установившемся процессе теплообмена.

Когда отношение < 2, что характерно для обычных металлических труб, из которых формируются теплообменники, это уравнение может быть заменено уравнением теплопроводности плоской стенки.