Примеры решения задач с комментариями

Задача 1.

Кривая производственных возможностей описывается уравнением X²+ Y² = 648. Функция полезности общества U = XY. Определить оптимальный объем про­изводства товаров X и Y.

Решение и комментарии.

Выпуск будет эффективен, если он одновременно будет максимизировать полезность покупателей и не выходить за границы производственных возможностей. Таким образом, граница производственных возможностей и кривая безразличия, отражающая максимально достижимый уровень удовлетворения потребностей, будут иметь одну общую точку Е (рис. 8.1). В этой точке предельная норма замещения будет равна предельной норме трансформации: MRS = MRT. Предельная норма трансформации характеризует то количество одного товара, от которого следует отказаться для производства дополнительной единицы другого товара: MRT_XY = -∆Y/∆X = -MC_X/MC_Y. Роль ограничения для максимизации полезности выполняет кривая производственных возможностей. П редельная норма трансформации товара Y в товар X будет равна: ∆Y/∆X = X/(648 – X²)^½. Предельная норма замены товара X товаром Y (из функции полезности) равна Y/X.

Решив систему уравнений:

X/(648 – X²)^½ = Y/X,

X² + Y² = 648,

Получим: X = 18 (количество товара X), Y = 18 (количество товара Y). Осуществим проверку: 18² + 18² = 648.

Полезность общества составит U = 18 · 18 = 324.

Графически решение будет выглядеть следующим образом (рис. 8.1).

Y

MRS = MRT

18 E

U = 324

X² + Y² = 648

0 18 X

Рис. 8.1. Эффективность выпуска

Ответ: X = 18; Y = 18.

Задача 2.

Предприятие производит продукцию, которая приносит пользу обществу, т.е. суммарный положительный эффект без учета загрязнения окружающей среды, равный TSB = 50Q – Q² и затраты (частные затраты) в размере TPC = 2Q + Q² и загрязняет окружающую среду. Совокупный ущерб, наносимый природе и обществу деятельностью предприятия, составляет TEC = 8Q.

а) найти объем выпуска (Q₁) и цену (P₁);

б) определить совокупные потери от отрицательного внешнего эффекта;

в) вычислить оптимальные с позиций всего общества объем выпуска (Q₂) и цену (P₂);

г) найти величину корректирующего налога на единицу продукции (t) и сумму корректирующего налога (T).

Решение и комментарии.

Рыночное равновесие устанавливается в точке, в которой предложение, равное предельным частным издержкам пересекается с кривой спроса, равной предельным общественным выгодам.

Определим кривую спроса, совпадающую с кривой предельной общественной выгоды D = MSB (рис. 8.2), поскольку внешние эффекты – это издержки или выгоды от рыночных сделок, не получившие отражения в ценах товаров, они показывают разность между социальными выгодами (издержками) и частными выгодами (издержками). Предельная общественная выгода может определяться суммарной оценкой предельной частной выгоды и предельной внешней выгоды. Найдем MSB как производную заданной в условии функции TSB = 50Q – 2Q². MSB = dTSB/dQ = 50 – 2Q.

Далее, найдем величину предельных общественных издержек MSC, которые представляют собой сумму предельных частных издержек MPC и предельных внешних издержек MEC.

Так как TSC = TPC + TEC = (2Q + Q²) + 8Q = 10Q + Q², то

MSC = dTSC/dQ = 10 + 2Q.

S₁ = MPC = 2Q + 2, S₂ = MSC = MPC + MEC = 2Q + 10.

Найдем точку равновесия (E₁) до введения корректирующего налога из равенства MSB = MPC, т.е.

50 – 2Q = 2Q + 2 → Q₁ = 12, P₁= = 50 – 2 · 12 = 26.

Найдем точку равновесия (E₂) после введения корректирующего налога t = MEC = 8 из равенства MSB = MSC, т.е.

50 – 2Q = 2Q + 10 → Q₂ = 10, P₂ = 50 – 2 · 10 = 30.

Вычислим совокупные потери от отрицательного внешнего эффекта, связанные с тем, что предельные частные издержки оказались ниже предельных социальных издержек. Они выражаются площадью треугольника ME₁E₂. Заметим, что ME₁ = t = 8. Высота этого треугольника, опущенная из точки E₂ на ME₁, равна разности Q₁ – Q₂= 2. Поэтому площадь треугольника ME₁E₂ будет равна 0,5t · (Q₁ – Q₂) = 8.

P S₂ = MPC + MEC

M S₁ = MRC

P 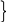₂ E₂ MEC

P 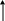₁ E₁

D = MSB

0 Q₂ Q₁ Q₂

Рис. 8.2. Действие корректирующего налога

Введение корректирующего налога позволит сократить перепроизводство товара с отрицательными внешними эффектами, тем самым трансформировать внешние эффекты во внутренние. Корректирующий налог на выпуск экономических благ позволяет повысить предельные частные издержки до уровня предельных общественных. Сумма налога составит T = t · Q₂ = 8 · 10 = 80.

Ответ: а) Q₁ = 12, P₁ = 26; б) 8; в) Q₂ = 10, P₂ = 30; г) t = 8, T= 80.

Задача 3.

В экономике производятся два товара – обозначим их А и В. Функция полезности общества зависит от выпуска товаров как U = QаQв. Товар А продается на мировом конкурентном рынке, где цена составляет 10. Предельные затраты единственного произво­дителя на товар А зависят от выпуска товара как: МСа = 0,1Qа. Проблема состоит в том, что отходы производства товара А повышают затраты и, сле­довательно, снижают выпуск товара В. Выпуск товара В зависит от выпуска товара А следующим образом: Qв = 100 – 0,01Qа².

1. Определите объем выпуска товаров А и В и уровень полезности об­щества, если государство не вмешивается в функционирование отраслей А и В;

2. Определите сумму количественного налога на единицу выпуска продукции А, которая обеспечивала бы максимум полезности общества.

Решение и комментарии.

1. Так как товар А продается на рынке совершенной конкуренции, то из условия максимизации прибыли MC_a = MR_a = P_a, решив систему уравнений, найдем объемы выпуска товара А и товара В.

M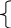 C_a = MR_a = P_{a ,} 0,1Q_a = 10,

Q_b =100 – 0,01Q_a², Q_b = 100 – 0,01·100²,

Q_a = 100, Q_b = 0.

Определим полезность общества от производства товаров в условиях свободного рынка U = Q_a · Q_b = 0.

Действие механизма несовершенной конкуренции не обеспечивает достижение комбинации выпуска товаров А и В, максимизации полезности общества. Причиной является отрицательный внешний эффект в результате отходов производства товара А.

2. Для определения эффективного объема выпуска товара А и товара В, обеспечивающего максимизацию полезности общества необходимо определить производную от функции полезности и приравнять к нулю.

(U)´ = 0, U´= (Q_a · (100 – 0.01Q_a²))´ = 100 – 0,03Q_a² = 0.

Оптимальный выпуск продукта А должен составлять Q_a ≈ 57,74, тогда оптимальный выпуск продукта В найдем, подставив в уравнение Q_b = 100 – 0,01· 57,74² ≈ 66,66. При этом полезность, достигаемая обществом, будет составлять U = 57,74 ∙ 66,66 = 3849.

Цену продукта А на внутреннем рынке определим исходя из условия равновесия фирмы на рынке совершенной конкуренции

MC_a1 = P_a1 = 0,1Q_a1, P_a1 = 0,1 ∙ 57,74 = 5,77.

Так как товар А продается на внешнем конкурентном рынке, цена на него устанавливается на уровне 10 ден. ед., то налог с единицы товара А составит t = P_a - P_a1 = 10 – 5,77 = 4,23.

Ответ: Q_a = 57,74; Q_b = 66,66; t =4,23.

Задача 4.

В стране бедных было 60 %, и они владели 40 % совокупного дохода, а богатых – 40 %, и они владели оставшимися 60 %:

а) построить кривую Лоренца;

б) найти коэффициент Джини, т.е. отношение площади фигуры, заключенной меду линией абсолютно равномерного распределения дохода и кривой Лоренца, к площади фигуры, заключенной под этой линией абсолютно равномерного распределения.

Решение и комментарии.

а) построим кривую Лоренца - кривую, отражающую фактическое распределение доходов (рис. 8.3)

б) найдем площадь треугольника ACH: S_ACH = 1/2 · 40 · 60 = 1200. Вычислим площадь трапеции CHKB: S_CHKB = 1/2 · (40 + 100) · 40 = 2800. За вычетом этой суммы из площади треугольника ABK имеем площадь треугольника ABC: S_ACBK = 4000, S_ABK = 1/2 · 100 · 100 = 5000. Следовательно, коэффициент Джини J = ((5000 – 4000)/5000) = 0,2.

Процент дохода

1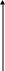 00 B

40

C

H K

A 60 100 Процент семей

Рис. 8.3. Кривая Лоренца

Ответ: 0,2.

Задача 5.

Спрос на продукцию естественной монополии задается функцией Q_D = 1 000 - P. Общие издержки монополии TC = Q² + 200Q + 5 000.

а) государство установило, что фирма не может увеличивать цену продукции выше 350. Найти прибыль естественной монополии в этих условиях;

б) фирма сумела доказать, что потолок цены занижен, и было установлено, что фирма не может увеличивать цену продукции выше 400. Найти прибыль естественной монополии при новом ограничении на цену продукции.

Решение и комментарии.

Из условия максимизации прибыли определим оптимальный объем выпуска для естественной монополии, для этого необходимо найти функции предельного дохода и предельных издержек фирмы и приравнять их: MR = 500 - Q и MC = 2Q + 200.

Отсюда 500 - Q = 2Q + 200, Q_e = 100, Следовательно, цена монополиста равна P_e = 450.

а) если государство фиксирует потолок цены на уровне 350, то фирма является ценополучателем при условии, что эта цена лежит не выше кривой спроса Q_D = 1 000 - 700 = 300 (рис. 8.4).

Это условие выполняется, так как цена товара равна предельным издержкам, следовательно, 350 = 200 + 2Q, отсюда объем выпуска равен Q = 75, прибыль составит 350 · 75 - 75² - 200 · 75 - 5 000 = 625;

б) если государство устанавливает потолок цены на уровне 400, то фирма будет действовать так, как будто ограничения отсутствуют. Это связано с тем, что точка равенства предельных издержек и цены товара P = MC = 400 лежит выше кривой спроса Q_D = 1000 - 800 = 200. Оптимум лежит в точке В, соответствующей пересечению кривых МС = МR и проекции этой точки на прямую P = 400.

Р

MC

4 50

P_b = 400

P_a = 350

В

Q_D

MR

0 100 200 Q

Рис. 8.4. Регулирование цен естественной монополии

Поэтому объем выпуска составит Q = 100, а цена P = 400. Следовательно, прибыль 400 · 100 - 100² - 200 · 100 - 5 000 = 5 000.

Ответ: 625; 5 000.