Математика для тк, хм, хн, см Аналитикалық геометрия және сызықтық алгебра элементтері (106)

А. есепте 3140 С) -4

А.есепте 21-3312041 Е) -53

А.есепте 52-1413224 С) -36

А. есепте 32-112141-1 D) 8

Аесепте -2413-23451 В) 93

А есепте 503-243121 С) -34

А есепте 31-122-14112234112 С) 35

А есепте -12132141-21-3212-13 D) -2

А есепте -2213-124131121-121 В) 100

А есепте 21-131142-13123421 D) 186

Аесепте 312-14211-122233-21 Е) -72

А есепте 41-2112133211-2321 А) -64

А есепте 30002100134-21321 D) 24

А есепте 1-123560000001234 Е) 0

Ж тап: 422214 D) (6;2)

Ж тап:Е) (2;2;1)

Ж таD) (-3;1;2)

Ж тап: -23-824412 С) (3;-1;-1)

-\, 1-35241234 В) 66

-\ егер, 123-1 А) -64

- \ 3541, Е) -453

-\, 12-13D) 0

-\, 34125-1121 В) -78

= detC \ x-1x-23 Е) x=-4/9

-\=12-1331, В) 48

- \ a=34-12 Е) 100

A=2-140м. 2А+3Х=0 ш. қ Х м есепте С) -12/3-8/31/3

A=2-13054 м. бе А-2В+3С D) 4-53551227

A=10-35матрицасы берілген А+А^Т- ны табу керек А) 2-3-310

A=3-145601-23м. б2А+3А^Т–ны табу керек С) 151311730-614-415

A=5-142 матрицалары берілгенАВ анықта С) 121260

A=3541матрицалары берілген ВА анықта В) 181353

A=132-141м. С=АВ м.с₂₃эл а D) -1

A=111410м С=АВ м с₂₁эл а В) 0

A=12-1 А мен В м.к есепте А) 123246-1-2-3

05200Матрицаны есепте а) 0000

$$$36 С

анықтауышының а₂₃ элементіне сәйкес минорын есепте

С) -1

$$$37 Е

берілген М₃₃- ді тап

Е) -1

$$$38 С

Dана матрица берілген А^-1 – ді тап

С)

$$$39 В

берілген А^-1 – ді тап

В) жоқ

$$$40 В

берілген кері матрицаның а₂₃– ді тап

В) -2/3

$$$41 D

матрицаның рангісін есепте

D) 2

$$$42 А

А(1;3;2) және В (5;8;-1) , - ны тап:

А) {4;5;-3}

$$$ 43D

А (4;2;1) және В (3;5;4) берілген. - ны тап:

D)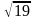

$$$ 44 А

және . -ны тап:

А) {5;12;19}

$$$45 В

-ны тап , егер және :

В) {7;0;-14}

$$$ 46 С

, берілген, -ны тап :

С) {-3;4;-1}

$$$ 47 Е

векторының ұзындығын тап:

Е) 3

$$$48 А

және векторлары берілген. -ны тап:

А) 6

$$$49 Е

және берілген, -ны тап:

Е 14

$$$50 В

, , болса, онда -ны тап:

В) 22

$$$51 С

, , болса, онда -ны тап:

С) 20

$$$52 А

, векторлары α мен β ның қандай мәнінде коллинеарлы болаDы?

А) α=3/4; β=-8/3

$$$53 D

, векторлары берілген, және базистік векторы бойынша жіктелуін тап:

D)

$$$54А

және векторларының арасындағы бұрыш 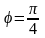, ал ұзындықтары , болса, онда скалярлық көбейтіндісін тап:

А

$$$55 D

, берілген, -ны тап:

D) 37

$$$56D

, векторларының скаляр көбейтіндісін тап:

D) 0

$$$ 57D

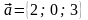, берілген. -ны тап

D) 10

$$$ 58 А

, берілген. векторлардың скалярлық көбейтіндісін тап:

A) -13

$$$ 59 С

, берілген. векторлардың скалярлық көбейтіндісін тап:

C) -84

$$$ 60 А

, және берілген. векторлардың скалярлық көбейтіндісін тап:

A) -524

$$$61 Е

және векторларының арасындағы бұрыштың косинусын тап:

Е)

$$$ 62C

Үшбұрыштың төбелері , , берілген, В нүктесінің ішкі бұрышын тап:

C) 45°

$$$ 63 Е

, , берілген, векторының

, және базисі бойынша жіктелуін табыңдар:

E)

$$$64 А

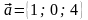, берілген, -ны тап:

A)

$$$65 Е

, берілген. Пр_ва - ны тап:

E) 6

$$$66 Е

, екі нүктесі берілген. векторының -векторына проекцияны тап:

E) 3

$$$67 Е

және векторларына салынған параллелограмның ауданын тап:

E)

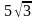
$$$ 68 А

және . векторларына салынған параллелограмның ауданын тап:

A)

$$$69 С

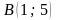, , , нүктелерінің арасынан түзуіне жататынын анықтаңдар:

C) А и D

$$$70 С

векторына перпендикуляр және нүктесінен өтетін түзудің теңтеуін анықтаңдар:

C)

$$$71 С

ОХ осінен және ОУ осінен -ге тең кеинді кесетін түзудің теңдеуін табыңдар:

C)

$$$72B

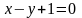және түзулерінің арасындағы бұрышты табыңдар:

B)

$$$73 А

, , нүктелері берілген. АВС үшбұрышының А төбесінен түсірілген медиананың теңдеуін табыңдар:

A)

$$$74 C

түзуінің теңдеуін нормальді түрге келтіріңдер:

C)

$$$75D

және параллель түзулерінің арақашықтығын табыңдар:

D)

$$$76 B

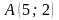нүктесінің түзуінен арақашықтығын табыңдар:

B) 2,2

$$$77 E

АВСүшбұрышының ВС қабырғасына параллель орта сызығының теңдеуін жазыңдар, егер , , болса:

E)

$$$78 B

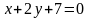және түзулерінің қиылысу нүктелерін табыңдар:

B)

$$$79 A

бұрыштық коэффициент және ОУ осінен нүктесіндегі қимасы берілген. Түзудің теңдеуін табыңдар:

A)

$$$80 D

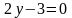түзуінің к бұрыштық коэффициентін табыңдар:

D) 0

$$$81 D

және түзулерінің арасындағы бұрышты табыңдар:

D)

$$$82 C

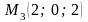, , нүктелерінен өтетін жазықтықтың теңдеуін табыңдар

C)

$$$83 E

нүктесінен жазықтығына дейінгі арақашықтықты тап:

E) 0

$$$84 D

нүктесінен жазықтығына дейінгі арақашықтықты тап:

D) 6

$$$85 A

жазықтығының нормаль векторының координаттарын анықтаңдар:

A)

$$$86 E

Төменде келтірілген қос теңдеулердің қайсысы параллель:

E) ,

$$$87 E

және нүктелері берілген, АВ кесіндісін қатынасымен бөлетін С нүктесінің абциссасын анықтаңдар:

E)

$$$88 C

векторына параллель және нүктесінен өтетін түзудің канондық теңдеуін анықтаңдар:

C)

$$$89B

жазықтығына перпендикуляр және нүктесін қиып өтетін түзудің параметрлік теңдеуін табыңдар

B) , ,

$$$90 C

Жазықтықтағы түзудің канондық түрінің дұрыс формуласын анықтаңыз:

C)

$$$91 A

Түзу жалпы теңдеулермен берілген: .

Бағыттаушы векторларының координаттарын анықтаңдар :

A)

$$$92 B

және түзулерінің арақашықтықтарын жазыңдар:

B) 6

$$$ 93 В

матрица берілген, кері матрицасын тап:

B)

$$$94 В

-ны анықта,егер ,

В) 48

$$$95 A

n m өлшемді матрица дегеніміз:

A) n жолы және m бағаны бар тік бұрышты сандар кестесі

**********

$$$96 D

Екі матрица А және В тең (А=В) деп аталады, егер:

D) олардың өлшемдері бірдей болса және сәйкес элементтері тең болса

**********

$$$97 C

А матрицасыныңα санына көбейтіндісін тап.

А= , α= 2

C)

$$$98 A

n-інші ретті матрицаның миноры деп (n-1)-ші ретті, былай табылған анықтауышты атаймыз:

A) i-ші жол менj-ші бағанды сызып тастағаннан кейін

**********

$$$99A

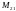А= матрицасы берілген. тап.

A)

**********

$$$100 D

элементінің алгебралық толықтауышы деп мына сан аталады:

D)

**********

$$$101 C

матрицасы берілген, элементінің алгебралық толықтауышын тап.

С) -3

$$$102 A

Матрицаның нөлден ерекше минорларының ең жоғарғы реті қалай аталады?

A) матрицаның рангы

**********

$$$103 B

жүйесінің шешімін тап, егер , ал болса:

B) x₁=8; x₂=7; x₃=9

**********

$$$104C

Теңдеулержүйесініңшешімінтап: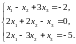

C) (-1;1;0)

**********

$$$105 D

Екі вектор коллинеар деп аталады, егер

D) олар бір түзудің немесе параллель түзулердің бойында жатса

**********

$$$106 B

және векторларының қайсысы коллине B)

**********

$$$107 A.

векторының модулі мына формуламен есептеледі:

A)

**********

$$$108 B

векторының модулін тап:

B)

**********

$$$109 B.

+ қосындысын тап, егер және болса.

B) (6;5;1)

**********

$$$110 E

А(6;-2;5) және В(-2;-4;6) нүктелері берілген. векторының координаттарын тап.

Е) (-8;-2;1)

**********

$$$111D.

және екі векторының скалярлық көбейтіндісі мынаған тең:

D) cos

$$$112 A

Екі нүкте арқылы өтетін түзудің теңдеуі:

A)

**************

$$$113D

матрицасы берілген, элементінің алгебралық толықтауышын тап.

D) 1

$$$114 A.

матрицасы берілген, элементінің алгебралық толықтауышын тап.

А) 3

$$$115 A

векторының модулін тап:

A) 3

$$$116 D

А= матрицасы берілген. тап.

D)

$$$117 E

А(4;-2;5) және В(6;-4;6) нүктелері берілген. векторының координаттарын тап.

Е) (2;-2;1)

$$$118 A

А(1;-2;5) және В(7;5;6) нүктелері берілген. векторының координаттарын тап.

A) (6;7;1)