1. Топологиялық кеңістік, анықтамасы, мысалдар

а) туынды топология

б) ашық және тұйық жиындар

в) топологияларды салыстыру 8

2. Топологияның базасы, метрикалық кеңістікте мысал

а) екінші саналымдылық аксиома. Саналымды база

б) Теорема (саналымды база, сепарабельділік)

3. Сеперабель топологиялық кеңістік, мысал.

а) бірінші саналымдылық аксиома, маңайлардың анықтауыш жүйесі, мысал.

б) саналымды база. Бірінші саналымды аксиомалы кеңістікке мысал.

4. Саналымды базалы Т кеңістігі және ашық бүркеу (теорема)

а) Байланысты кеңістік, мысал.

б) сеперабель кеңістік және саналымды база (теорема)

5. Бірінші саналымдылық аксиома, маңайлардың анықтауыш жүйесі, мысалы

а) Саналымды база, қасиеттері

б) Метрикалық кеңістіктер және саналымдылық аксиомалары

6. Бүркеу, ішбүркеу, мысал.

а) Компакты жиын, қасиеттері (теорема), компакт.

б) Хаусдорф кеңістігіндегі компакты жиын (теорема)

7. Тізбектердің жинақтылығы.

а) Жанасу нүктесі және бірінші саналымдылық аксиомалы Т кеңістігі.

б) Жанасу нүктесіне жинақталатын тізбегі жоқ кеңістікке мысал

8. Бейнелеу(оператор) үзіліссіздігі, анықтама, мысал.

а) Оператор үзіліссіздігі туралы теорема

б) Оператордың үзіліссіздігі және топология (теорема).

9. Гомеоморфизм.

а) Өзара гомеоморфты метрикалық кеңістіктерге мысал

б) Геоморфизм және кеңістіктердің топологиялық, метрикалық қасиеттері

10. – аксиома. емес кеңістікке мысал.

а) кеңістіктегі шектік нүкте

б) кеңістіктегі ақырлы жиын

11. – аксиома. Хаусдорф кеңістігі мысал

а) Хаусдорф кеңістігі болмайтын кеңістікке мысал

б) Хаусдорф және регуляр кеңістікті салыстыр

12. – аксиома

а) регуляр емес Хаусдорф кеңістігіне мысал.

б) Регуляр және Хаусдорф кеңістіктерін салыстыр

13. – аксиома, мысал

а) Регуляр кеңістік

б) Нормаль кеңістікке мысал

14. Топологияны анықтау жолдары.

а) Саналымды база және кеңістіктің сеперабельділігі (теорема)

б) Метрикалық кеңістікте топологияны анықта

15. Топологиялық кеңістіктің метрикалануы.

а) П.С. Урысон теоремасы (дәлелсіз)

б) Нормаланған кеңістікте топологияны анықта

16. Теорема (оператор үзіліссіздігі).

а) Оператордың үзіліссіздігі мен топологиялардың байланысы (күштілік және әлсіздік)

б) Оператордың үзіліссіздігі және тұйық жиындар (теорема)

17. Лемма ( )

а) Шектік нүктенің анықтамасы

б) Жанасу нүктесі, қасиеттері.

18. Компактылық және центрленген жүйе, Теорема.

а) Салыстырмалы топология

б) Жиынның компактылығы

19. Теорема(T - компакты, шектік нүкте).

а) Центрленген жүйе

б) Компактылық және саналымды компактылық түсініктерін салыстыр (теорема)

20. Теорема (Т – компакты, тұйық жиын)

а) Тұйық жиын

б) Компакт

21. Теорема (Компактты жиынның ішжиыны).

а) Компактылық анықтамасы, мысал

б) Ашық, тұйық жиындар

22. Теорема (Хаусдорф кеңістігіндегі компакты жиын).

а) Тұйық және ашық жиындар, екі жақтылық қатынас.

б) Жанасу нүктелері, қасиеттері.

23. Теорема (Компакт және нормаль кеңістік).

а) аксиомасы

б) Нормаль кеңістікке мысал

24. Теорема (Компакты жиынның үзіліссіз бейнесі).

а) Компакты кеңістіктегі үзіліссіз функционал

б) Компакттылық және саналымды компакттылық

25. Теорема (Хаусдорф кеңістігіне өзара бірмәнді үзіліссіз бейне).

а) Геоморфизм, мысал.

б) Үзіліссіз бейнелеу, анықтамасы, қасиеттері.

26. Сызықтық топологиялық кеңістіктер, лемма (нөлдің маңайлары).

а) СТК-дегі маңай түсініктері

б) Маңайлар базасы

27. Саналымды нормалы кеңістіктер, мысалдар.

а) Нормалардың келісімділігі.

б) Саналымды нормалы кеңістікте метрика анықта.

28. Саналымды Гильберт кеңістіктері, мысал.

а) Нормаланған толық кеңістіктердің кемімелі тізбегі.

б) Саналымды нормалы кеңістіктің толықтық шарты.

29. СТК-тің анықтамасы, қасиеттері.

а) Локаль дөңес кеңістіктер,қасиеттері.

б) СТК шенелген және локаль шенелен жиындар, қасиеттері.

30. Теорема (СТК - тің нормалануы), дәлелсіз

а) Хаусдорф кеңістігі, мысал.

б) Дөңес маңай

31. Саналымды базалы T – кеңістікте б.ж. тығыз жиынды көрсет.

а) Екінші саналымдылық аксиомасы

б) Сеперабель кеңістік, мысал

32. Метрикалық кеңістікте топология базасын тұрғыз.

а) Метрикалық кеңістіктегі ашық шар

б) Топология базасы, мысал

33. жиынында тек қана тұрақты тізбек жинақты болатын топология анықта

а) Кеңістіктің топологиясы

б) Тізбектің жинақтылығы

34. – де 0-жанасу нүктесіне жинақты тізбек жоқ болатын топология анықта

а) Жанасу және шектік нүктелер

б) Кеңістіктің топологиясы

35. Бірінші саналымдылық аксиомалы Т-кеңістіктерінің қасиеті.

а) Маңайлардың анықтауыш жүйесі

б) Жанасу нүктесі

36. – кеңістікте нүкте қандай жиын?

а) Ашық, тұйық жиындар, қосалқылық қатынастар.

б) Нүктенің , жиынның маңайы (СТК-те).

37. Ақырлы жиынның шектік нүктесі болатын Т – кеңістікке мысал.

а) Шектік нүкте

б) Тізбектің жинақтылығы

38. Хаусдорф кеңістігі болмайтын кеңістікті көрсет а) Хаусдорф аксиомасы, Хаусдорф кеңістігіне мысал.

б) Нүктенің маңайы (СТК-те).

39. Регуляр болмайтын Хаусдорф кеңістігіне мысал келтір.

а) Регуляр кеңістік

б) - бөлектену аксиомасы

40. Нормаль кеңістікке мысал келтір.

а) бөлектену аксиомасы

б) Хаусдорф кеңістігі болмайтын -кеңістікке мысал.

41. Локаль дөңес кеңістік, мысал

а) Жиынның орнықтылануы

б) Нөлдің маңайының орнықтылануы маңай бола ма?

42. Лемма. СТК-дегі жиынның шенелгендігі.

а) Жұтушы жиын, мысал.

б) Тізбектің жинақтылығы

43. Лемма. СТК Х Хаусдорф кеңістігі болу үшін

а) Нөл нүктесінің маңайлары (СНК).

б) Хаусдроф аксиомасы

44. Компакты кеңістіктегі үзіліссіз функционал (теорема)

45. Компакты кеңістіктегі ақырсыз жиын (теорема)

46. Компакты кеңістіктегі тұйық жиын (теорема)

47. Хаусдорф кеңістігіндегі компакт. (теорема)

48. Компакты кеңістіктің үзіліссіз бейнесі (теорема)

49. бөлектеу аксиомасы орынсыз кеңістікті көрсет?

50. Регуляр емес Хаусдорф кеңістігін анықта.

51. Сеперабель кеңістік, мысалдар.

52. жиынында тек қана тұрақты тізбек жинақталатын топология келтір.

53. Жанасу нүктесіне жинақты тізбек болмайтын Т – кеңістік тұрғыз.

54. Ақырлы жиын тұйық болатын Т – кеңістік қандай?

55. Хаусдорф кеңістігі болмайтын кеңістік тұрғыз

56. Жанасу нүктесіне жинақты тізбек табылмайтын Т – кеңістікке мысал келтір.

57. Rⁿ - Евклид кеңістігіндегі компакты жиындар

58. Сеперабель кеңістіктер, қасиеттері, мысалдар.

59. кеңістік болмайтын кеңістік тұрғыз

60. С[a,b]-үзіліссіз функциялар кеңістігіндегі компакты жиындар.

1. Топологиялық кеңістік, анықтамасы, мысалдар

а) туынды топология

б) ашық және тұйық жиындар

в) топологияларды салыстыру

Анықтама 1. Х-жиыны берілсін. Осы жиынның топологиясы деп- төменгі щарттарды қанағаттандыратын осы жиынның іш жиындарының жүйесін айтады.

1. Х- жиыны өзі және -ға тиісті.

2. -ға тиісті жиындарының қаншасыныңда (саны ақырлы және ақырсыз) бірігуі -ға тиісті. ( )

3. -ға тиісті жиындарының кез келген ақырлы және қиылысуы -ға тиісті. ( )

Мысал. Метрикалық кеңістікте анықталған ашық жиындар Анықтама 1-дегі 3 аксиоманы қанағаттандырады. Демек метрикалық кеңістікте топологияляқ кеңістік болып есептелінеді. Бірақ, маңызы үлкен болсада топологияляқ кеңістіктің дербес түрі болып саналанады.

а) Х- жиыны өзін жиынды және Х жиынының барлық іш жиындарын ашық жиындар деп есептесек, онда Ан. 1-дегі 1-3 аксиомалар орындалады. Бұндай топология туынды топология деп аталады.

б) жүйесіне тісті жиындар ашық жиындар деп аталады.

жиынның толықтауышы тұйық жиын деп аталады. Сонымен кез келген ашық жиынның толықтауышы тұйық жиын деп аталады.

Анықтама 1- ден қосалқылық қасиет бойынша:

1. -ға тиісті тұйық жиындарының қаншасыныңда (саны ақырлы және ақырсыз) бірігуі де тұйық жиын.

2. 

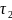с) Х жиынында және топологиялары берілсін, егер болса, онда күштірек топология ( ), ал әлсізірек топология деп аталады

2. Топологияның базасы, метрикалық кеңістікте мысал

а) екінші саналымдылық аксиома. Саналымды база

б) Теорема (саналымды база, сепарабельділік)

Анықтама. Ашық жиындардың жүйесі T кеңістігі топологиясының базасы деп аталады,егер T кеңістігіндегі әрбір ашық жиын жүйесі жиындарының (ақырлы не ақырсыз)бірігуі болса.

Мысалы,метрикалық кеңістікте барлық ашық шарлардың (центрлері кез келген нүктедегі және кез келген радиусы)жиыны база болады.

Сонымен T кеңістігінде оның қайсыбір базасы көрсетілсе,онда оның топологиясы анықталады,ол базасы жиындарының бірігулерінің жүйесі болады.

Төменгі қасиеттер T=(X, ) топологиялық кеңістіктің кез келген базасына тең:

1.Әрбір x X нүктесі кемінде бір G жиынына тиісті.

2.Егер x G₁ G₂ , G₁ , G₂ , болса онда x G₃ G₁ G₂ болатын G₃ жиыны табылады.

Шынында X жиынының өзі топологиясына тиісті ашық жиын болғандықтан,ол базаға тиісті қайсыбір жиындардың бірігуі болады.Бұдан 1)қасиет шығады.Ал 2)пункттегі G₁ G₂ ашық жиын,сондықтан ол да базаға кіретін қайсыбір жиындардың бірігуі.Демек,2)қасиет те орынды.

Төменде саналымды жиыннан аспайтын кемінде бір базасы бар топологиялық кеңістіктер класының маңызын көреміз.Ондай кеңістіктер саналымды базалы немесе екінші саналымдылық аксиомалы топологиялық кеңістіктер деп аталады.

Егер T топологиялық кеңістікте саналымды база бар болса,онда барлық жерде тығыз саналымды жиын да табылытынына,демек, T сеперабель кеңістік болатынына көз жеткізейік. - саналымды база дейік.Онда әрбір жиынынан бір x_n нүктеден алып,X = саналымды жиынын құрастырамыз.Осы саналымды жиын барлық жерде тығыз болады. Болмаған жағдайда G = T - ашық жиынында X-тың ешбір нүктесі табылмас еді.Бұл мүмкін емес,себебі G ашық жиын ретінде базаның қайсыбір жиындарының бірігуі болар еді,ал x_n

Метрикалық кеңістіктер үшін дәлелденген сөйлемге кері сөйлем де орынды.

Егер M-сеперабель метрикалық кеңістік болса,онда оның саналымды базасы бар.Шынында сеперабель кеңістікте барлық жерде тығыз X = саналымды жиын бар болғандықтан S ашық шарлары саналымды база береді.Мұндағы n,m бір бірінен байланыссыз натурал сандар.Осыдан төменгі теорема шығады.

1-теорема.Метрикалық кеңістік саналымды базалы болу үшін оның сеперабель кеңістік болуы қажет және жеткілікті.

Дәлелі. Метрикалық кеңістік топологиялық кеңістік болғандықтан, егер саналымды базисі бар болса, онда метрикалық кеңістік сепарабель болатындығы жоғарғы топологиялық кеңістік айтылғанынан шығады. Сонымен барлық сеперабель метрикалық кеңістіктер екінші саналымдылық аксиомалы кеңістіктер болды.

Х-метрикалық кеңістігінде саналымды барлық жерде тығыз N={ } жиыны бар дейік, яғни ( ) ⇒ S( ), n,m- кез келген натурал сандар, ашық шарлар жүйесі саналымды базис болады.

Метрикаық кеңістіктер сияқты барлық жерде тығыз болатын саналымды ішжиыны бар топологиялық кеңістік сеперабель кеңстік деп аталады.