3) Уравнения, решаемые разложением на множители одной части, если другая 0

а) sin2x – sinx = 0

sinx( 2cosx – 1) = 0; sinx = 0; cosx = 1/2; Ответ: x = пk, x = п/3 + 2пk, k

б) sin7x + sin3x = 3cos2x

2sin5x cos2x – 3cos2x = 0; cos2x(2sin5x – 3) = 0; cos2x = 0; sin5x = 3/2; Ответ: x = п/4 + пk/2 ,k

в) cos3x = sin10x

cos3x – cos(п/2 – 10х) = 0; - 2sin(п/4 – 7/2х)sin(-п/4 + 13/2х) = 0

Ответ: x = п/ 14 – 2/7 пk, x = п/26 + 2/13пk, k .

4) Уравнения, решаемые с помощью формул понижения степени.

а) sin²x – sin²3x = cos²4x – cos²2x

cos6x – cos2x = cos8x – cos4x; - 2sin4xsin2x = - 2sin6xsin2x; 2sin2x sinx cos5x = 0

Ответ: x = пk ; x = п/10 + пk/5 ,k

б) cos²x + cos²2x – cos²3x – cos²4x = 0

cos2x + cos4x – cos6x – cos8x = 0; 2cos3xcosx – 2cos7xcosx = 0; 4cosx sin2x sin5x = 0

Ответ: x = пk/5 ; x = п/2 + пk ,k

5) Уравнения, решаемые с помощью универсальной тригонометрической подстановки ( f(sinx, cosx, tgx, ctgx) )

Замечание: эти формулы сужают ОДЗ. Может произойти потеря корней, т. к. tgx/2 не существует при х = п + 2пк. Следовательно, это решение надо проверить отдельно. Лучше, по возможности, не использовать эти формулы.

1 + cosx = sinx + tgx ОДЗ: x

Проверяем подстановкой х = п + 2пк (0 = 0) – решение

Ответ:

6) Уравнения, решаемые выделением тригонометрической единицы: sin²x + cos²x = 1

а) sin⁴x + cos⁴x = sin2x – 1/2

1 – 2sin²xcos²x = sinxcosx – 1/2;t² + 2t – 3 = 0;D = 16;sin2x = - 3; 1; 2x = п/2 + 2пk ,k

Ответ: x = п/4 + пk ,k

б) sin⁶x + cos⁶x – cos²2x = 1/16

(sin²x)³ + (cos²x)³ = 1 – 3/4 sin²2x; 16 – 12sin²2x – 16cos²2x – 1 = 0; 4sin²2x = 1; sin2x =

Ответ: x = п/12 + пk/2 ,k

7) Уравнения, в которых используются алгебраическая сумма и произведение тригонометрических функций.

а) sin2x – sinx – cosx – 1 = 0

sinx + cosx = t; t² = 1 + 2sinxcosx; sin2x = t² – 1; t² – t – 2 = 0;D = 9; t = 2; - 1

sinx + cosx = 2; sinx = 1 и cosx = 1 sinx + cosx = - 1; sin(x + п/4) = - 1/

Ответ: x = (-1)^{к +1}п/4 – п/4 + пk, k

б) ОДЗ: x

sinx - cosx = sinxcosx; sinx - cosx = t; t² = 1 - 2sinxcosx; sin2x = t² – 1; t² – t – 2 = 0; D = 8; ; sinx - cosx = ; sinx - cosx = ; sin(x - п/4) =

Ответ: x = (-1)^к + п/4 + пk, k

8) Уравнения, решаемые с использованием формул произведения функций.

а) 2sinx sin3x = cos2x

cos2x – cos4x – cos2x = 0; cos4x = 0; Ответ: x = п/8 + пk/4 ,k

б) сosx sin7x = cos3x sin5x

1/2(sin8x + sin6x) = 1/2(sin8x + sin2x); sin6x – sin2x = 0; sin2x cos4x = 0; sin2x = 0; cos4x = 0

Ответ: x = пk/2 ; x = п/8 + пk/4 ,k

9) Уравнения вида asinx + bcosx = c, где a, b, c 0.

1) Переход к половинному аргументу (основной способ решения)

а) sinx + cosx = 1

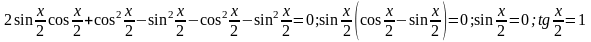
Ответ: x = 2пk ; x = п/2 + 2пk , k

б) 4sinx + 3cosx = 5

Ответ: x = 2arctg 1/2 + 2пk, k .

в) 2sinx - 3cosx = 3

Ответ:

г) 3sinx - 4cosx = 2

2) Деление обеих частей на (если «подгоняется» под формулу)

а) sinx + cosx = 1

; Ответ: x = (-1)^к п/4 – п/4 + пk, k

б) Ответ: x = (-1)^к п/12 + п/18 + пk/3, k

3) Применение универсальной тригонометрической подстановки

а) sinx + cosx = 1 Проверяем х = п + 2пк; (- 1 1)

Ответ: x = 2пk ; x = п/2 + 2пk ,k

б) 2sinx - 3cosx = 3 Проверяем х = п + 2пк; (3 = 3 – решение уравнения)

Ответ: .

4) Введение вспомогательного угла asinx + bcosx = Эти формулы удобно применять, если

а) sinx + cosx = 1

sin(x + arctg 1) = 1; sin(x + п/4) = 1/ Ответ: x = (-1)^к п/4 – п/4 + пk, k

б) сos3x - sin3x = 1

2sin(-3x + arctg ) = 1; sin( п/6 – 3x) = 1/2 Ответ: x = (-1)^к+1 п/18 + п/18 – пk/3, k

в) 2сos5x - 5sin5x =

(5x + arctg2,5 ) = ; сos (5x + arctg2,5 ) - = 0; = 0 Ответ:

г) Найти множество значений функции у = 2sinx - 3cosx

2sinx - 3cosx =