Задание 1. Расчет допусков размеров, входящих в размерные цепи

Задача 1. Перерасчет размеров допусков от заданной базы

Рассмотрим сложную размерную цепь.

1 2 3 4 5 6

1. Метод полной взаимозаменяемости

Разбиваем сложную цепь на ряд элементарных цепей

1 2 3 4 5 6

Первая цепь: В₄ = А₄; А₃ = А_∆;

В₃ = А _∆ + В₄ = 270 + 115 = 385 мм;

ES = ES + EI = 0 мм;

EI = EI + ES = – 0,35 + 0,3 = – 0,05 мм;

B₃ = 385_-0,05.

Вторая цепь: А₂=А_;

B₂ = A_∆+ B₂ = 135 + 385 = 520 мм;

ES = ES + EI = 0,2 + (-0,05) = + 0,15 мм;

EI = EI + ES = – 0,2 + 0 = – 0,2 мм;

B₂ = 520 .

Третья цепь: А₁=А_;

B₁ = A_∆ + B₂ =40 + 520 = 560 мм;

ES = ES + EI = 0,5 + (- 0,2) = + 0,3 мм;

EI = EI + ES = 0 + 0,15 = 0,15 мм;

B₁ = 560 .

Полученная цепь будет иметь вид

2. Теоретико-вероятностный метод

Разбиваем сложную цепь на ряд элементарных.

Первая цепь: В₄ = А₄; А₃ = А_∆;

В₃ = А_∆ + В₄ = 270 + 115 = 385 мм;

ТВ₃ = мм;

Е_сВ₃ = Е_сВ₄ + Е_сА_∆ = 0,3/2 + (-0,35/2) = -0,025 мм;

ES_В3 = Е_сВ₃ + ТВ₃/2 = -0,025 + 0,180/2 = + 0,065 мм;

EI_В3 = Е_сВ₃ - ТВ₃/2 = -0,025 - 0,180/2 = -0,115 мм;

В₃ = .

Вторая цепь: А₂ = А_∆;

В₂ = А_∆ + В₃ = 135 +385 = 520 мм;

ТВ₂ = мм;

Е_сВ₂ = Е_сВ₃ + Е_сА_∆ = + 0,065 – 0,115/2 – 0 = -0,025 мм;

ES_В2 = Е_сВ₂ + ТВ₂/2 = -0,025 + 0,385/2 = + 0,154 мм;

EI_В2 = Е_сВ₂ – ТВ₂/2 = -0,025 - 0,358/2 = -0,204 мм;

В₂ = .

Третья цепь: А₁ = А _∆;

В₁ = А_∆ + В₂ = 40 + 520 = 560 мм;

ТВ₁ = мм;

Е_сВ₁ = Е_сВ₂ + Е_сА_∆ = + 0,154 – 0,204/2 + 0,5/2 =

= +0,225 мм;

ES_В1 = Е_сВ₁ + ТВ₁/2 = +0,225 + 0,35/2 = + 0,4 мм;

EI_B1= E_cB₁ – TB₁/2 = +0,225 – 0,35/2 = +0,050 мм;

В₁ =

Полученная цепь будет иметь вид

Задача 2. Определение допусков составляющих размеров

В данной цепи размеры А₁, А₂, А₃, А₄ является увеличивающими, а А₅, А₆, А₇ – уменьшающими. ТА_∆ = 0,5 мм.

1. Метод полной взаимозаменяемости

ТА_ј = a x i,

где а- количество единиц допуска; i- единица допуска.

i =

где

отсюда

ТА_Δ = a_m x i_Δ;

TA_Δ =

a_m = .

Подставив значения, получим:

*

* Для расчета подкоренных выражений и выбора квалитета точности используйте прил. 3,4.

По рассчитанному значению a_m в соответствии с ГОСТ 25346-82 принимаем квалитет IT8 и по заданным номинальным размерам и квалитету* выбираем соответствующие им значения допусков

ТА₁ = 0,046 мм; ТА₂ = ТА₅ = ТА₇ = 0,063 мм;

ТА₃ = 0,072 мм; ТА₄ = 0,089 мм; ТА₆ = 0,097 мм.

Правильность выбора допусков проверяем по выражению

;

0,046 + 3х0,063 + 0,072 + 0,089 + 0,097<0,500;

0,493<0,500.

Условие выполняется.

Для увеличивающих размеров назначаем допуски по Н8, для уменьшающих – по h8.

А₁ = 55^+0,046; А₂ = 125^+0,063; А₃ = 240^+0,072; А₄ = 340^+0,089;

А₅ = 140_-0,063; А₆ = 440_-0,097; А₇ = 135_-0,063.

2. Теоретико-вероятностный метод

При решении данной задачи теоретико-вероятностным методом формула нахождения a_m будет иметь вид

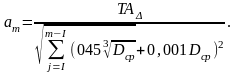
Полагаем, что погрешности составляющих и замыкающего размеров подчиняются закону нормального распределения.

Подставив значения, получим

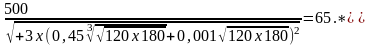
* Для расчета подкоренных выражений и выбора квалитета точности используйте прил. 3,4.

По рассчитанному значению а_m в соответствии с ГОСТ 25346-82 принимаем квалитет IT10 и по заданным номинальным размерам и квалитету * выбираем соответствующие им значения допусков

TA₁ = 0,120 мм; TA₁ = TA₅ = TA₇ = 0,160 мм;

TA₃ = 0,185 мм; TA₄ = 0,230 мм; TA₆ = 0,250 мм.

0,491<0,500

Условие выполняется.

Для увеличивающих размеров назначаем допуски по Н10, для уменьшающих – по h10.

A₁ = 55^+0,120; А₂ = 125^+0,160; А₃ = 240^+0,185; А₄ = 340^+0,230;

А₅ = 140_-0,160; А₆ = 440_-0,250; А₇ = 135_-0,160.