
- •Тема 5 натуральные числа и нуль
- •5.1. Этапы развития понятия натурального числа
- •5.2. Натуральный ряд и его свойства. Счет
- •5.2. Натуральный ряд и его свойства. Счет
- •5.3. Теоретико-множественный смысл натурального числа и нуля
- •5.3. Теоретико-множественный смысл натурального числа и нуля 107
- •5.4. Натуральное число как результат измерения величины 109
- •5.4. Натуральное число как результат измерения величины
- •5,5. Способы записи чисел
- •5.6. Особенности десятичной системы счисления
112
НАТУРАЛЬНЫЕ
ЧИСЛА И НУЛЬ
Примечание.
Заслушиваются
доклады и сообщения, предварительно
подготовленные студентами, на темы:
«Возникновение и развитие нумерации»,
«Системы счисления разных народов»,
«Запись чисел в Древней Руси»,
«Происхождение десятичной системы
счисления».
Трудности
в развитии науки были преодолены с
созданием в Древней Индии десятичной
системы записи чисел и введением
понятия нуля. Первыми заимствовали
у индийцев цифры и десятичную систему
арабы, поэтому ее часто называют
арабской.
В
десятичной системе счисления для записи
чисел используются 10 знаков (цифр):
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Для
краткости записи цифры пишут друг
за другом, а значение
цифры
зависит от ее места, считая справа
налево.
Например:
5437 — краткая запись числа «пять тысяч
четыреста тридцать семь». Подробная
запись этого числа выглядит так:
5000+400+30+7 или: 5 • 103+4
• 102+3
• 10+7.
Десятичной
записью числа х
называется его представление в виде:
х=ап
■
10п+апА
■
Ю"’1+...+<*,
• Ю'+яо ' Ю°,
где
ап,
а„.х,
..., а{,
а0
принимают значения:
0, 1,2, 3,
4, 5, 6, 7, 8, 9, и
Числа
1, 10, 102,
103,
..., 10"'1,
10” называются разрядными
единицами
соответственно первого, второго и т.д.
разряда.
Краткая
запись числа выглядит так: апапЛ
...a{aQ
.
Данная
система записи чисел называется
десятичной,
так как 10 является основанием
системы,
то есть 10 единиц одного разряда
составляют 1 единицу следующего
разряда.
В
целях подготовки к усвоению десятичной
системы счисления старшие дошкольники
знакомятся с цифрами, учатся считать
группами (в том числе десятками).
Младшие школьники, знакомясь с десятичной
системой счисления, выполняют задание:
«Представь число в виде суммы разрядных
слагаемых», учатся называть разряды и
классы.
Три
первых разряда образуют класс единиц,
следующие три разряда — класс тысяч,
затем идет класс миллионов и др. (рис.
91).
Для
записи любого числа достаточно 10 цифр.
Для называния чисел в пределах миллиарда
достаточно 16 различных слов: один, два,
три, четыре, пять, шесть, семь, восемь,
девять, десять, сорок,5.6. Особенности десятичной системы счисления
| Классы |
|
миллионов |
тысяч |
единиц |
|||||||
Разряды |
|
сот. млн. |
дес. млн. |
ед. млн. |
сот. тыс. |
дес. тыс. |
ед. тыс. |
сот. |
дес. |
ед. |
|
Рис.
91
Некоторые
вопросы наименования и записи чисел
можно рассматривать уже с дошкольниками.
Например.
«Отсчитаем
10 палочек. Перевяжем их. Это десяток.
Десяток можно называть «дцатъ».
Положим на десяток палочек еще одну.
Всего одиннадцать палочек — «один
на дцатъ».
«Возьмем
две связки. Это два десятка. Можно
сказать «два
дцатъ».
Объяснение
происхождения названий чисел второго
десятка, счет десятками дает хорошую
подготовку дошкольникам к усвоению
десятичной системы счисления в курсе
математики в школе.
Задание
69
Представьте
число 345 679 в виде суммы разрядных
слагаемых.
Покажите
краткую запись числа 8- 10*+6-10+8.
Запишите
наибольшее и наименьшее трехзначные
числа.
Сумма
цифр двузначного числа равна 9, причем
десятков в два
раза
больше единиц. Найдите это число.
В
десятичной системе счисления действия
с многозначными числами выполняют по
правилам, называемым алгоритмами.
Запись сложения, вычитания и умножения
выполняют столбиком,
а деления — уголком,
это умение становится доступным уже
младшим школьникам. В основе вычислений
лежат некоторые теоретические знания.
Например, при сложении используются:
способ
записи числа в десятичной системе
счисления;
законы
сложения;
таблица
сложения однозначных чисел.
Задание
70
Вспомните
правила сложения, вычитания, умножения,
деления
многозначных
чисел в десятичной системе счисления.
Приведите
примеры.
8
- 7975






114
НАТУРАЛЬНЫЕ
ЧИСЛА И НУЛЬ
Опорный
конспект к теме №5 «НАТУРАЛЬНЫЕ ЧИСЛА
И НУЛЬ»
Счет
Измерение
Возникновение
числа
Этапы
развития понятия числа
Непосредственное
сравнение множеств.
Использование
множеств-посредников.
Возникновение
понятия натурального числа.
Создание
систем счисления.
Возникновение
науки о числах — арифметики.
Свойства
натурального ряда
имеется
начальный элемент — число 1;
за
каждым числом непосредственно следует
только одно число;
каждое
последующее число на 1 больше
предыдущего числа, а каждое предыдущее
на 1 меньше последующего (л±1). |
|
Сложение |
Вычитание |
а+Ь=с, где а, b — слагаемые, с — сумма |
а—Ь=с, где а — уменьшаемое, b — вычитаемое, с — разность |
Если АпВ=0, то A jB= С, где а — число элементов в множестве А, b — число элементов в множестве В, с — число элементов в множестве С. |
Если ВаА, то А\В=С, где а — число элементов в множестве А, b — число элементов в множестве В, с — число элементов в множестве С. |
А В у - ■ ■ |
в с |
С А+В=С, где А=а Е, В=Ь Е, С=с Е, Е — единица длины |
л А—В=С, где А=а Е, В=Ь Е, С=с Е, Е — единица длины |

115
Вопросы
для самоконтроля к теме № 5
Назовите
этапы развития понятия числа.
Назовите
функции натурального числа.
Что
называют натуральным рядом?
Какие
функции натурального ряда вы знаете?
Что
называют отрезком натурального ряда
NJ
Что
такое счет?
Для
чего служит счет?
Чем
является натуральное число с
теоретико-множественных позиций?
Что
такое нуль с теоретико-множественных
позиций?
Каков
смысл отношения «меньше» с
теоретико-множественной точки зрения?
Каков
смысл суммы целых неотрицательных
чисел с теоретико-множественных
позиций?
Каков
смысл разности целых неотрицательных
чисел с теорети- ко-множественных
позиций?
Каков
смысл натурального числа, полученного
в результате измерения длины отрезка?
Каков
смысл суммы натуральных чисел, полученных
в результате измерения длины отрезка?
Каков
смысл разности натуральных чисел,
полученных в результате измерения
длины отрезка?
Что
такое система счисления?
Какие
системы счисления называются
позиционными?
Какие
системы счисления называются
непозиционными?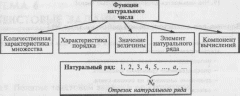
116
НАТУРАЛЬНЫЕ
ЧИСЛАМ НУЛЬ
19.
Что называется десятичной записью
числа?
Задания
для самостоятельной работы к теме №5
Приведите
примеры деятельности дошкольников в
соответствии с этапами развития числа:
непосредственное
сравнение множеств,
опосредованное
сравнение множеств,
сравнение
множеств на основе счета,
запись
чисел и действий.
Придумайте
правила счета для дошкольников в целях
предотвращения ошибок.
Сформулируйте
вопросы дошкольникам с целью уточнения
их представлений о количественном и
порядковом смысле числа.
Выполните
перевод записи числа в другую систему
счисления: а) 1769 в римскую; 6) MDCCCLXXVI
в
десятичную.
Придумайте
диалог с младшими школьниками,
показывающий происхождение названий
чисел второго десятка и круглых чисел
в пределах 100.
Найдите
в энциклопедиях названия классов и их
значение в десятичной системе
счисления и продолжите последовательность:
единицы, тысяча, миллион, миллиард,
триллион, квадриллион, квинтиллион,
..., гугол.
Подготовьте
сообщения на темы:
«Как
люди научились считать»,
«Возникновение
и развитие нумерации»,
«Системы
счисления разных народов»,
«Запись
чисел в Древней Руси»,
«Происхождение
десятичной системы счисления».
