2Разработка математических моделей

2.1Описание исследуемой системы

Рассмотрим систему поддержания положения звена манипулятора по данным, получаемым с гироскопа. Силы и моменты, действующие на систему, представлены на рисунке ниже (Рисунок 2 .5).

Рисунок 2.5 - Силы и моменты, действующие на систему

Здесь M – момент на валу двигателя;

M* – момент внешней силы, приложенной к системе;

α – текущий угол поворота звена манипулятора по данным датчика манипулятора;

G – сила тяжести, действующая на систему;

L – длина невесомого звена; m – масса, сосредоточенная на конце звена.

Общий момент, действующий на систему можно описать следующим образом:

Структурная схема системы показана на рисунке ниже (Рисунок 2 .6).

Рисунок 2.6 – Структурная схема исследуемой системы

Здесь α – текущий угол поворота звена манипулятора по данным датчика манипулятора;

ω – текущая угловая скорость по данным датчика манипулятора;

a – текущее ускорение по данным датчика манипулятора;

α* – реальный угол наклона звена манипулятора по данным гироскопа;

u – управляющее воздействие на двигатель звена манипулятора.

Более подробно схема, показанная выше (Рисунок 2 .6) представлена на следующем рисунке (Рисунок 2 .7).

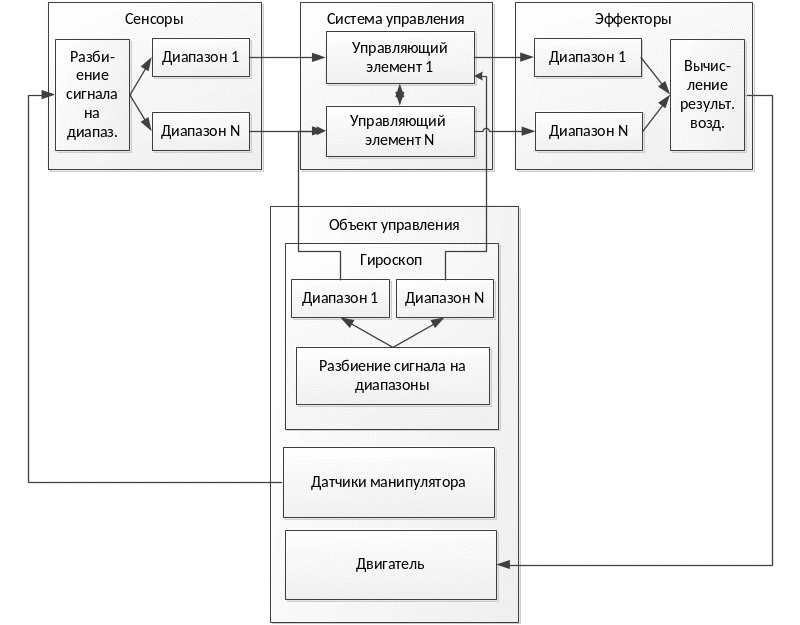
Рисунок 2.7 – Функциональная схема исследуемой системы

Здесь схема регулятора из работы [2,3] дополнена данными с гироскопа, которые аналогично другим сенсорным данным разбиваются на диапазоны и поступают в систему управления в качестве желаемого значения положения звена манипулятора, где влияет непосредственно на афферентные нейроны.

2.2Модель нейрона с взаимным влиянием ионных механизмов друг на друга

Модель нейрона, представленная в работах [4,5], была модифицирована для обеспечения возможности применения эффекта временной суммации импульсов [6] при использовании модели нейрона в контуре управления. Была модифицирована модель ионного механизма участка мембраны нейрона.

Возбуждающими и тормозными входами нейрона являются входы множества моделей возбуждающих и тормозных синапсов для каждого из участков мембраны .

Результирующие значения влияния синапсов на механизмы гиперполяризации ( ) и деполяризации ( ) получаются в результате суммирования:

, .

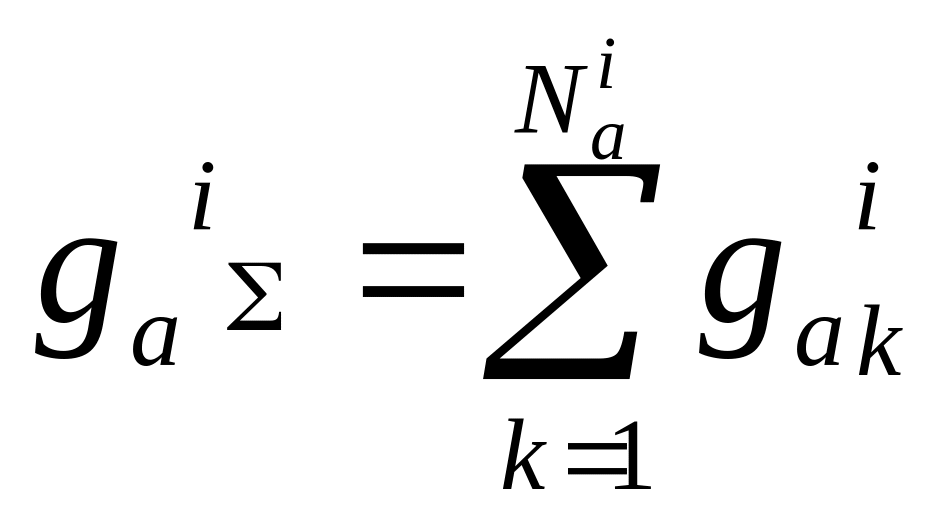Уравнения описания новой модели ионного механизма деполяризации представлены ниже.

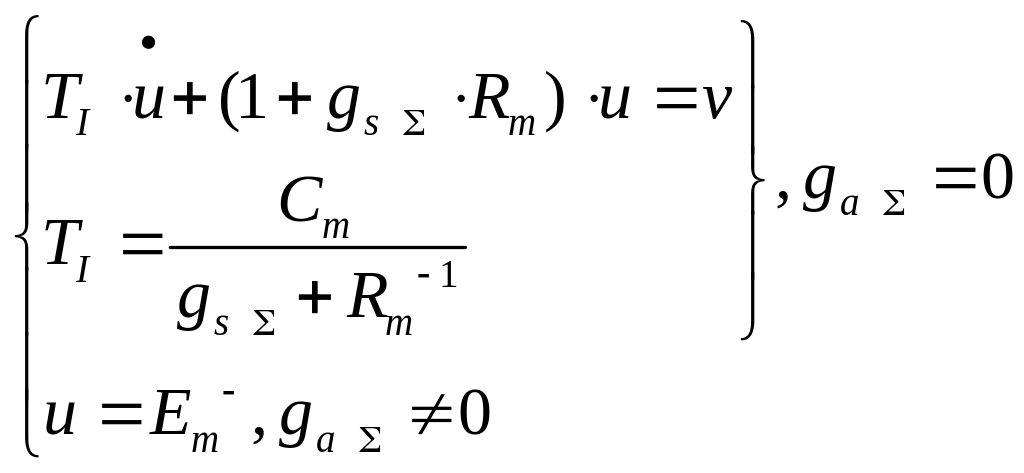
Начальные условия: u(0)=0.

Для ионного механизма гиперполяризации уравнения аналогичны с точностью до перемены мест влияний возбуждающих и тормозных синапсов и E_m^- на E_m⁺.

Иными словами отличие заключается в том, что в каждом участке мембраны, при активации возбуждающего синапса, ионный механизм противоположного знака принудительно сбрасывается в состояние покоя. При такой реализации нейрон получает возможность при увеличении емкости мембраны (большая постоянная времени ионных механизмов) проводить суммацию сигналов на больших интервалах времени, и при этом сохранить быструю реакцию на изменение характера входного воздействия (возбуждение или торможение). В задачах регуляции движения, где типичным поведением нейрона является попеременная работа на возбуждение и торможение в составе контуров антагонистов это позволит осуществить более гибкое управление.

Введение взаимного влияния ионных механизмов участков мембраны имеет смысл, если необходимо увеличить инерционные свойства мембраны нейрона. В дальнейших экспериментах мы будем менять емкость мембраны нейрона в сторону ее увеличения, и исследовать эффекты временной суммации сигналов и их влияние на работу нейрона в задачах регуляции движения.

В таблице ниже (Таблица 2 .1) приведены значения параметров моделей всех функциональных элементов нейрона. Эти значения использовались для всех экспериментов описываемых ниже. Значения параметров выбирались таким образом, чтобы наиболее наглядно продемонстрировать возможности качественного описания реакций естественных нейронов с различной организацией мембраны.

Таблица 2.1 – Значения параметров модели нейрона

Синапс

Постоянная времени выделения медиатора τs=0.001 c. Постоянная времени распада медиатора τd=0.01 с. Амплитуда входного сигнала Ey=1. Коэффициент влияния эффекта пресинаптического торможения ξ=0. Эквивалентное сопротивление канала (“вес” синапса) Rs=1∙108 Ом.

Ионный механизм мембраны дендритов

Эквивалентное сопротивление мембраны в состоянии покоя Ом. Эквивалентное сопротивление в состоянии перезаряда Ом. Эквивалентная емкость мембраны: номинальная (в соответствии с предыдущими работами): Ф; увеличенная: Ф; Начальные вклады {Em}={Em+, Em-} в мембранный потенциал ионных механизмов в состоянии покоя: Em+=1, Em-=-1.

Ионный механизм мембраны сомы

Эквивалентное сопротивление мембраны в состоянии покоя Ом. Эквивалентное сопротивление в состоянии перезаряда Ом. Эквивалентная емкость мембраны Ф.

Генератор потенциала действия

Порог нейрона P=0.001. Постоянная времени, определяющая инерцию генераторного механизма =0.005 с. Амплитуда выходного сигнала Ey=1. Коэффициент обратной связи F перезаряда мембраны для нейрона с числом участков мембраны сомы L=1: F=1.7. Коэффициент F подбирается так, чтобы длительность импульса на выходе нейрона приблизительно равнялась 0.001с, соответствующей длительности импульсов, генерируемых биологическим нейроном.