1.2Модели биологических нейронов

Помимо рассмотренных в п.1.1.2.2 моделей формальных нейронов, имеющих сильнейшую формализацию и примитивизацию функций, что делает их далекими от моделирования реальной работы нейронов, разработано большое число моделей, описывающих нейрон с точки зрения химии протекающих процессов.

Так в модели Ходжкина-Хаксли (Hodgkin - Huxley model) исследуется характер протекания тока через мембрану и моделируется распространение возбуждения. Данная модель учитывает действие трех различных типов ионного тока (натриевого, калиевого и тока утечки) на возбудимость мембраны. Более современные физиологические модели отличаются от модели Ходжкина-Хаксли в основном учетом большего количества типов ионов (модель коркового нейрона с шумом, Connor–Walter–McKown model и др.) или более узкой направленностью исследования, например, модели для понимания распространения волны возбуждения в отдельных участках проводящей системы сердца (модели МакАлистера-Нобла-Цяня и Билера-Рейтера, Алиева-Панфилова, Зимана). При этом во всех перечисленных выше моделях при выводе законов изменения проводимостей мембраны, внимание в первую очередь обращалось на достижение точного совпадения расчетных и экспериментальных данных, что затрудняет их применение для решения задач управления. Схематично классификация моделей, описывающих нейрон с точки зрения химии протекающих процессов, представлена ниже (Рисунок 1 .3).

Рисунок 1.3 – Модели нейрона, основанные на описании химии протекающих процессов

Недостатком обозначенных нейросетей является то, что теоретическое описание информационных процессов в них, как правило, существенно отличается при рассмотрении и анализе каждой конкретной системы. Далее более подробно рассмотрим некоторые из этих моделей.

1.3Теория возбуждения Ходжкина – Хаксли

В основе данной теории лежит эквивалентная схема замещения мембраны представленная на Рисунок 1 .4.

Рисунок 1.4 - Эквивалентная схема мембраны Ходжкина - Хаксли

Принимается, что полный ток через мембрану нейрона является суммой емкостного тока , тока за счёт перемещения ионов натрия внутрь клетки , тока за счет перемещения ионов калия из клетки во внеклеточную жидкость , и небольшого тока за счет перемещения ионов других веществ, в частности, ионов хлора . Сопротивления и являются переменными, сопротивление - постоянным, удельная емкость мембраны обозначена через C. , , - равновесные потенциалы мембраны для равной концентрации соответствующих ионов в клетке и внеклеточной среде. Напряжение U определяет потенциал мембраны. Полный ток через мембрану определяется следующей формулой:

(1.1)

Обычно при раздражении клетки при помощи микроэлектрода можно считать, что полный ток через мембрану равен нулю. Тогда потенциал действия (по Ходжкину и Хаксли) определяется дифференциальным уравнением

(1.2)

Ионные токи могут быть выражены через значения проводимостей следующим образом:

(1.3)

где , , , , а - абсолютное значение потенциала покоя.

Ионные проводимости и существенно изменяются при развитии возбуждения. Для того, чтобы описать закон изменения проводимостей , Ходжкин и Хаксли предложили ввести вспомогательную переменную n, подчиняющуюся следующему дифференциальному уравнению:

(1.4)

где - некоторые фиксированные значения, являющиеся функциями деполяризующего напряжения V. Проводимость , тогда может быть записана в виде , где - некоторая константа.

Для параметров и были определены следующие эмпирические зависимости:

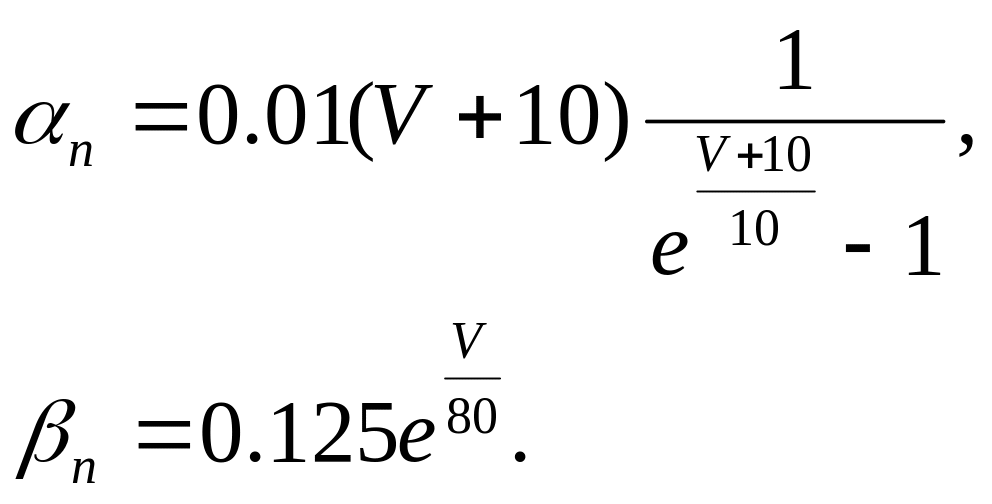
Закон изменения проводимости в модели Ходжкина-Хаксли, может быть представлен через решение системы двух дифференциальных уравнений первого порядка

(1.5)

где - постоянные, зависящие от деполяризующего напряжения.

Проводимость представляется функцией этих переменных - , где - некоторая константа.

Были установлены следующие эмпирические зависимости для постоянных уравнений (1.5):

При выводе законов изменения проводимостей мембраны для ионов натрия и калия, внимание в первую очередь обращалось на достижение точного совпадения расчетных и экспериментальных данных.

Как видно из изложенного, теория возбуждения нервной клетки Ходжкина-Хаксли весьма сложна. Рассмотренная теория, уделяя основное внимание мембране нейрона, не рассматривает детально синаптический аппарат, оперируя лишь следствиями его воздействия на мембрану нейрона.