Вариант 9
№1.
Решить
систему трех уравнений с тремя
неизвестными методами Крамера и Гаусса:
№2
Определить
производные
,
пользуясь формулами дифференцирования:
а)
б)
в)
г) 
д)
№3
Найти
интегралы:а)
;
б)
;
в)
.
№4
Вычислить
определенный интеграл с точностью до
0,001 путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда
№5
Найти
общее решение (общий интеграл)
дифференциального уравнения первого
порядка
Вариант 10
№1.
Решить
систему трех уравнений с тремя
неизвестными методами Крамера и Гаусса:
№2
Определить
производные
,
пользуясь формулами дифференцирования:
а)
б)
в)
г) 
д)
№3
Найти
интегралы:а)
;
б)
;
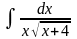в)
.
№4
Вычислить
определенный интеграл с точностью до
0,001 путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда
№5
Найти
общее решение (общий интеграл)
дифференциального уравнения первого
порядка
.
Вариант 11
№1.
Решить
систему трех уравнений с тремя
неизвестными методами Крамера и Гаусса:
№2
Определить
производные
,
пользуясь формулами дифференцирования:
а)
б)
в)
г) 
д)
№3
Найти
интегралы:а)
;
б)
;
в)
.
№4
Вычислить
определенный интеграл с точностью до
0,001 путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда
№5
Найти
частное решение дифференциального
уравнения, удовлетворяющее указанным
начальным условиям
,
.
Вариант 12
№1.
Решить
систему трех уравнений с тремя
неизвестными методами Крамера и Гаусса:
№2
Определить
производные
,
пользуясь формулами дифференцирования:
а)
б)
в)
г) 
д)
№3
Найти
интегралы:а)
;
б)
;
в)
.
№4
Вычислить
определенный интеграл с точностью до
0,001 путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда
№5
Найти
частное решение дифференциального
уравнения, удовлетворяющее указанным
начальным условиям
,
.
Вариант 13
№1.
Решить
систему трех уравнений с тремя
неизвестными методами Крамера и Гаусса:
№2
Определить
производные
,
пользуясь формулами дифференцирования:
а)
б)
в)
г) 
д)
№3
Найти
интегралы:а)
;
б)
;
в)
.
№4
Вычислить
определенный интеграл с точностью до
0,001 путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда
№5
Найти
частное решение дифференциального
уравнения, удовлетворяющее указанным
начальным условиям
,
.
Вариант 14
№1.
Решить
систему трех уравнений с тремя
неизвестными методами Крамера и Гаусса:
№2
Определить
производные
,
пользуясь формулами дифференцирования:
а)
б)
в)
г) 
д)
№3
Найти
интегралы:а)
;
б)
;
в)
.
№4
Вычислить
определенный интеграл с точностью до
0,001 путем предварительного разложения
подынтегральной функции в ряд и почленного
интегрирования этого ряда
№5
Найти
частное решение дифференциального
уравнения, удовлетворяющее указанным
начальным условиям
,
.