
- •Теорія автоматичного керування
- •4.1. Математичне моделювання
- •4.2. Моделі вв для одноканальних систем
- •4.3. Передавальна функція
- •4.4. Моделі вв багатоканальних систем
- •4.5. Моделі вв збурених систем
- •5.1. Перетворення Лапласа та його основні властивості.
- •5.2. Передавальна функція.
- •5.1. Перетворення Лапласа та його основні властивості
- •5. Диференціювання і інтегрування оригіналу
- •6. Дифренціювання та інтегрування зображення
- •7. Запізнення зображень і оригіналів
- •6.2. Амплітудна та фазова частотні характеристики
- •6.3. Логарифмічні частотні характеристики
- •7.1. Перехідна характеристика
- •Сигнали на вході і на виході при побудові перехідної характеристики:
- •7.2. Вагова характеристика
- •7.3. Усталений режим
- •7.4. Статична характеристика
- •8.1. Поняття простору станів і моделі стан-вихід
- •8.2. Моделі вхід-стан-вихід
- •8.1. Поняття простору станів і моделі стан-вихід
- •8.2.Моделі вхід-стан-вихід
- •8.2.1. Розглянемо одноканальну систему (об’єкт керування), що описується диференціальним рівнянням:
- •9.2. Умовні позначення
- •4. Перенесення суматора через ланку
- •5. Перенесення вузла через ланку
- •9.4. Типова одноконтурна система
- •10.2. Аперіодична (інерційна) динамічна ланка
- •10.3. Диференційна динамічна ланка
- •10.4. Інтегруюча динамічна ланка
- •10.5. Ланка запізнювання
- •11.2. Аперіодична ланка іі порядку
- •11.3. Коливальна ланка
Теорія автоматичного керування
Лекції
Змістовий модуль 2
Лекція 4. Математичні моделі вхід-вихід (ВВ)
4.1. Математичне моделювання.
4.2. Моделі ВВ для одноканальних систем.
4.3. Передавальна функція.
4.4. Моделі ВВ багатоканальних систем.
4.5. Моделі ВВ збурених систем.
4.1. Математичне моделювання
Для того, щоб управляти яким-небудь об'єктом, необхідно знати як пов'язані вхідні і вихідні змінні. При зміні інформації на вході об'єкта змінюється його внутрішній стан і, як наслідок, виходи. Це означає, що існує деяке правило, за яким елемент перетворює вхідні змінні и в вихідні y: y = А [и]. Це правило, по суті, являє собою деяку модель об'єкта.
Математичною моделлю динамічної системи прийнято називати сукупність математичних символів, що однозначно визначають розвиток процесів у системі, тобто її рух.
В залежності від використовуваних символів розрізняють аналітичні та графоаналітичні моделі. Аналітичні моделі будуються з допомогою буквених символів, графоаналітичні - допускають застосування графічних позначень.
Типи моделей
|
|
В залежності від використовуваних символів
|
аналітичні |
графоаналітичні |
|
В залежності від типу сигналів |
безперервні
|
дискретні |
|
В залежності від використовуваних операторів |
лінійні |
нелінійні |
|
В залежності від використовуваних операторів |
часові |
частотні |
|
У залежності від способу отримання |
теоретичні |
експериментальні |
|
4.2. Моделі вв для одноканальних систем
Модель вхід-вихід (ВВ) - це опис зв'язку вхідних і вихідних сигналів динамічної системи. |
|
При описанні системи керування в цілому вхідним сигналом САК служить завдання y*(t) = g (t), а вихідним - змінна y (t).
|
y(t)
g(t)
САК
|
При описанні об'єкта керування вхідним сигналом є керуючий вплив u(t), а вихідним - регульована змінна y (t). Для інших блоків – можливо замість u(t) → х(t) або інш.
|
OK
y(t)
u(t) |
Лінійна модель вхід-вихід одноканальної
динамічної системи

 (4.1)
(4.1)
 ,
-коефіцієнти (параметри моделі),
0
≤ m
<n,
n-порядок
моделі,
,
-коефіцієнти (параметри моделі),
0
≤ m
<n,
n-порядок
моделі,
 ,
,
 .
.
(4.1) - лінійне неоднорідне диференційне рівняння n-го порядку.
Права частина цього рівняння визначає зовнішню дію на систему.
Cтаціонарні системи - значення параметрів незмінні:
 ,
,
 .
.
Нестаціонарні системи - параметри є функціями часу,
 .
.
У
разі, коли
 ,
рівняння (4.1) називається приведеним.
,
рівняння (4.1) називається приведеним.
Для спрощення застосовують операторну форму.
Оператор диференціювання
 ,
,
 .
.Рівняння ВВ (4.1) в операторній формі:

=
 . (4.2)
. (4.2)
Або
 (4.3)
(4.3)
де
a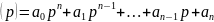 ,
(4.4)
,
(4.4)
b . (4.5)
. (4.5)
Загальне
рішення лінійного неоднорідного
диференційного рівняння n-го
порядку з постійними коефіцієнтами є
сумою загального рішення
 відповідного однорідного рівняння і
частинного рішення
відповідного однорідного рівняння і
частинного рішення
 неоднорідного
рівняння:
неоднорідного
рівняння:

Відповідне однорідне рівняння:
0.
Однорідне рівняння описує динаміку системи при умові, що зовнішня дія на неї відсутня. Для його вирішення використовують підстановку Ейлера, а саме:
 Ця
підстановка приводить розв’язання
лінійного диференційного рівняння до
алгебраїчного рівняння
Ця
підстановка приводить розв’язання
лінійного диференційного рівняння до
алгебраїчного рівняння
 exp(pt)=0.
exp(pt)=0.
Або
 = 0.
(4.6)
= 0.
(4.6)
У виразі а(p) і b(p) мають спеціальні назви.
а(р) - характеристичний поліном диференціального рівняння (4.1) або власний оператор
a .
Корені рівняння (4.6) а(р)=0 називають полюсами системи (4.1).
У
загальному випадку рівняння а(р)=0
має
п
комплексних коренів
 .
.
b(p) -характеристичний поліном правої частини (4.1)
або оператор дії:
b .
Корені рівняння b(р)=0 називають нулями системи (4.1).
У
загальному випадку рівняння b(р)=0
має
m
комплексних коренів
 .
.












