4. Аналітичне подання булевих функцій. Функціонально повні системи булевих функцій

Розглянуті найпростіші булеві функції дозволяють будувати нові булеві функції за допомогою узагальненої операції, яка називається операцією суперпозиції. Фактично операція суперпозиції полягає в підстановці замість аргументів даної функції інших булевих функцій (зокрема інших аргументів). Наприклад, із функції f₁ (x₁, x₂) за допомогою підстановок x₁ = f₃ (x₅, x₄) і х₂ = x₃ замість аргументів х₁ і x₂ відповідно отримаємо функцію f₁ (f₃ (х₅, x₄), x₃). Остання від змінних x₁ і x₂ уже не залежить.

Операція суперпозиції дозволяє побачити якісний перехід від п, рівного одиниці, до п, рівного двом. Дійсно, суперпозиція функцій одного аргументу породжує функції також одного аргументу. Суперпозиція функцій двох аргументів дає можливість будувати функції будь-якої кількості аргументів (в наведеному прикладі побудована функція трьох аргументів).

Суперпозиція булевих функцій зображається у вигляді логічних формул. Однак необхідно відмітити:

- одна і та ж функція може бути представлена різними формулами;

- кожній формулі відповідає своя суперпозиція і, отже, своя схема з’єднання логічних елементів;

- між формулами подання булевих функцій і схемами, які їх реалізують, існує взаємно однозначна відповідність.

Будь-яка двійкова функція, за винятком функції тотожного нуля, може бути подана як суперпозиція трьох функцій І, АБО та НІ.

4.1. Досконала диз’юнктивна нормальна форма (дднф)

Оскільки між множиною аналітичних подавань і множиною схем, які реалізують булеву функцію, існує взаємно однозначна відповідність, відшукування канонічної форми подання булевої функції являється початковим етапом синтезу схеми, що її реалізує. Найбільш широке розповсюдження отримала досконала диз’юнктивна нормальна форма (ДДНФ). Наведемо визначення конституенти одиниці – поняття, яке буде далі широко використовуватись.

Визначення. Конституентою одиниці називається функція f (x₁, x₂, …, x_n), яка приймає значення 1 тільки на одному наборі.

Конституента одиниці записується у вигляді терма, тобто у вигляді логічного множення п різних булевих змінних, деякі з яких можуть бути з використанням заперечення. Наприклад, f = – елементарний логічний добуток, який являється конституентою одиниці змінних x₁, x₂, x₃ і x₄, приймає значення 1 тільки на одному наборі 1001. Зрозуміло, що на решті 15 наборах ця функція приймає значення 0.

Якщо згадати, що диз’юнкція приймає значення 1, коли хоча б одна із змінних приймає значення 1, то можна легко виразити будь-яку булеву функцію як диз’юнкцію конституент одиниці, які відповідають тим наборам, на яких функція приймає значення 1. У більш загальному вигляді це можна записати наступним чином (4.1):

,

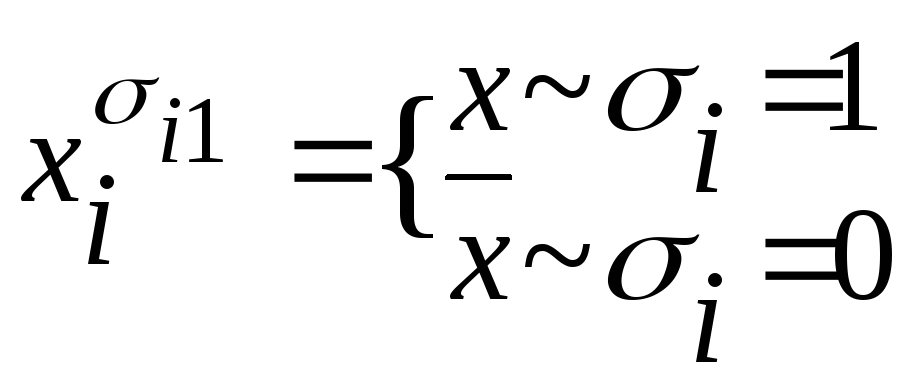де і . (4.1)

Таблиця 4.1
x1	x 2	x3	f1	f2
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Ця форма і є ДДНФ. Відмітимо, що набори, на яких функція f приймає значення 1, часто називаються одиничними, а інші – нульовими наборами. Виписувати в ДДНФ доцільно тільки конституенти одиниці, тобто те, що відповідає одиничним наборам. Подання булевої функції в ДДНФ єдине.

Приклад 1. Випишемо ДДНФ для функцій, заданих таблицею істинності (табл. 4.1).

.