4. Calculation of the power angular characteristics for the post-emergency mode

In the after-failure mode (mode II), the circuit is disconnected line w, on which a short circuit occurred.

Determine the resistance of the system:

Determine the mutual resistance:

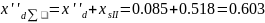
The power characteristic in the post-emergency mode will take the following form:

5. Calculation of the angular power characteristics for the emergency mode

For the emergency mode, we consider 2 types of faults: three-phase and two-phase on the ground. At the scene of the accident, a shunt with resistance x_Δ is inserted. For the three-phase operation, x_Δ = 0, for two-phase operation x_Δ = x_2∑ // x_0∑.

Define the resulting resistance of the circuits of the inverse and zero sequences. In the reverse-sequence substitution circuit, the resistance of the transformers T1, T2 and the line W remain unchanged, and the resistance of the generator G1 is recalculated. EMF of source is equal to zero.

Determine the negative sequence resistance of the generator G1:

We construct the negative sequence substitution circuit.

Figure 3.5 — Negative sequence substitution circuit

Determine the total reactance of the negative sequence:

Determine the resistance of the zero sequence, taking into account the fact that in the circuit of substitution of the zero sequence of resistance of the two-circuit line, W increases by 5 times.

Determine the resistance of the zero sequence of a two-circuit line W:

Determine the resistance of the transformers T1 and T2

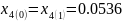
The resistance of the generator G1 in the zero sequence replacement circuit is not taken into account because it is located behind the transformer T1, whose windings are connected in a triangle. We compose the zero sequence replacement circuit (Figure 4.8)

Figure 3.6— zero sequence replacement circuit

Determine the total reactance of the zero sequence:

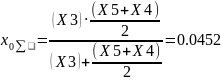
Determine the resistance of the shunt at a two-phase short-circuit to earth:

Then construct the replacement circuit of the emergency mode:

Figure 3.7— Emergency mode replacement circuit

Carry out the further transformation of the emergency mode replacement circuit

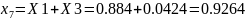
Then construct the transformed replacement circuit

Figure 3.8 — Transformed replacement circuit

— three-phase short circuit

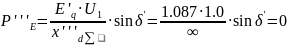
At three-phase short circuit the power transmission to the system GS is impossible.

— two-phase short circuit to the ground

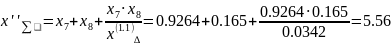
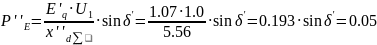
6. Calculation of the limiting short-circuit breaking angle and the cut-off time limit

To determine the limiting cut-off angle, the criterion of dynamic stability is used. The acceleration area should be equal to the area of possible braking. The limiting angle determines the equality of these areas.

Expression for determining the cut-off angle:

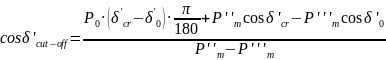
— three-phase short circuit

— two-phase short circuit to the ground

It can be seen from the obtained results that the system is unstable under both types of faults and requires a trip according to the condition of maintaining dynamic stability.

The nature of the change in the angle δ’ (t), along which it is possible to find the limiting time t_cut-off of the short-circuit breaker or the time t_max reaching an angle δ’_max with the oscillations of the rotor of the equivalent generator, is determined by the solution of the differential equation with respect to the motion of the rotor of the equivalent generator

The inertia constant of the equivalent generator G:

We solve the differential equation by the method of successive intervals. We take the step of integration Δt = 0.05 s. In this case, the coefficient k (in electric degrees) will be equal to

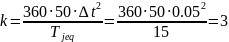
The increment of the angle in the first interval is :

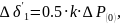
where the excess power at the beginning of the interval is: