Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА

(национальный исследовательский университет)»

РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ

КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЙ MATLAB

САМАРА 2012

Министерство образования и науки

Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА

(национальный исследовательский университет)»

РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ

КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЙ MATLAB

Методические указания к лабораторной работе

САМАРА 2012

УДК 519.6

Составитель: А.А. Федотов

Решение уравнений в среде компьютерных вычислений MATLAB: Метод. указания / – Самар. гос. аэрокосм. ун-т.; сост. А.А. Федотов; Самара, 2012. 20 с.

В методических указаниях изложены основные сведения об особенностях решения математических уравнений в среде компьютерных вычислений MATLAB. Рассматриваются типовые примеры использования встроенных функций среды MATLAB для решения алгебраических и трансцендентных уравнений, систем линейных уравнений и дифференциальных уравнений. Приведены порядок выполнения работы и требования к отчету.

Методические указания предназначены для студентов очно-заочной формы обучения, обучающихся по специальности 201000 «Биотехнические системы и технологии» и выполняющих лабораторные работы по дисциплине “Информационные технологии”. Подготовлены на кафедре радиотехники и медицинских диагностических систем.

Ил. 1 Библиогр. 5 назв.

Печатаются по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П. Королева

Рецензент: И.А. Кудрявцев

Цель работы: изучить реализацию основных методов решения математических уравнений в среде компьютерных вычислений MATLAB.

Задачи:

1. Изучить синтаксис языка программирования MATLAB для решения алгебраических и трансцендентных уравнений, систем линейных уравнений, а также дифференциальных уравнений.

2. Используя полученные теоретические сведения, выполнить задания лабораторной работы и подготовить отчет.

1 Теоретические основы работы

1.1 Решение алгебраических и трансцендентных уравнений

Алгебраическим уравнением называют уравнение вида: P(x)=0, где P(x) – многочлен отличный от нулевого. Степенью алгебраического уравнения называют максимальную степень его многочленов. Значения переменных x₁, x₂, …, x_n которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями алгебраического уравнения.

Для нахождения корней алгебраических уравнений в среде MATLAB существует функция roots, имеющая следующий синтаксис:

x=roots(p)

где: p – вектор коэффициентов полинома P(x), x – выходной вектор корней полинома P(x).

Трансцендентное уравнение – уравнение, не являющееся алгебраическим, как правило, такие уравнения содержат показательные, логарифмические, тригонометрические, обратные тригонометрические функции и т.д. Решение трансцендентных уравнений определяют численными методами.

Для нахождения корней трансцендентных уравнений вида f(x)=0 в среде MATLAB применят функцию fzero, имеющую следующий синтаксис:

x=fzero(‘funname’, [a b], options)

где: funname – имя файл-функции в среде MATLAB, определяющей искомую математическую функцию f(x); a, b – границы интервала изоляции значения корня уравнения; options – параметры, управляющие процессом вычисления.

Другой формой обращения к функции fzero является:

x=fzero(‘funname’, x0, options)

где: x0 – начальное приближение к корню уравнения.

Решение трансцендентных уравнений следует начинать с построения графика функции f(x), что позволит визуально оценить интервалы изоляции корня уравнения или его начальное приближение.

Для решения трансцендентных уравнений также может использоваться функция fsolve, имеющая следующий синтаксис:

x=fsolve(@funname, x0, options)

где: x0 – начальное приближение к корню уравнения, funname – имя файл-функции в среде MATLAB, определяющей искомую математическую функцию f(x), options – параметры, управляющие процессом вычисления.

1.2 Решение систем линейных уравнений

Система из m-уравнений с n неизвестными следующего вида называется системой линейных уравнений, причем x_j – неизвестные, a_ij – коэффициенты при неизвестных, b_i – свободные коэффициенты:

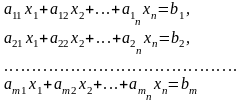
Также система линейных уравнений может быть описана с помощью матриц и представлена в следующем виде:

A∙X=B

где: X – вектор неизвестных, A – матрица коэффициентов при неизвестных или матрица системы, B – вектор свободных членов системы или вектор правых частей.

Матрица (A|B), которая формируется путем конкатенации исходной матрицы коэффициентов A и вектора-столбца свободных членов B, называется расширенной матрицей системы.

Если все свободные члены системы нулевые, то система линейных уравнений является однородной системой линейных уравнений, в противном случае система называется неоднородной.

Совокупность всех решений системы (x₁, x₂,…, x_n) называется множеством решений или решением системы уравнений. Однородные системы линейных уравнений вида A∙X=0 всегда разрешимы, при этом решения (x₁=0, x₂=0,…, x_n=0) называются тривиальными решениями, поэтому проблема решения однородных систем уравнений сводится к нахождению нетривиальных решений.

Система линейных уравнений может не иметь ни одного решения, в этом случае она называется несовместной. Если система линейных уравнений имеет решение, то она называется совместной. Совместная система называется определенной, если у нее есть единственное решение и неопределенной, если решений больше чем одно. Совокупность всех решений неопределенной системы уравнений называется ее общим решением, а одно конкретное решение – частным решением. Частное решение, полученное из общего решения при нулевых значениях свободных коэффициентов, называется базисным решением.

При определении совместности системы уравнений важную роль играет понятие ранга матрицы. Пусть дана матрица A размером n×m, вычеркиванием из нее некоторых строк или столбцов можно получить квадратные матрицы k-го порядка, определители которых называются минорами порядка k матрицы A. Наивысший порядок не равных нулю миноров матрицы A называют рангом матрицы и обозначают r(A). При элементарных преобразованиях (перестановка строк матриц, умножение строк на число, отличное от нуля и сложение строк) ранг матрицы не меняется. Определение ранга расширенной матрицы системы линейных уравнений необходимо при определении совместности системы уравнений:

1) система n линейных уравнений с m переменными является несовместной, если: r(A|B)>r(A);

2) система n линейных уравнений с m переменными является совместной, если: r(A|B)=r(A); при этом, если r(A|B)=r(A)=m, то система имеет единственное решение, если r(A|B)=r(A)<m, то система имеет бесконечно много решений.

Определение совместности системы линейных уравнений формулируется теоремой Кронекера-Капелли: система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Данная теорема имеет два важных следствия:

1) количество главных переменных равно рангу системы и не зависит от её решения;

2) если ранг совместной системы равен числу переменных данной системы, то она определена.

В системе MATLAB для нахождения ранга матрицы используется команда следующего вида:

r=rank(A)

где: A – исходная матрица, r – величина ранга матрицы A.

Существует множество методов нахождения решений систем линейных уравнений, все методы разделяются на точные и приближенные. Метод решения относится к точным, если с его помощью можно найти решение в результате конечного числа арифметических и логических операций. В частности, к точным методам решения систем линейных уравнений относятся правило Крамера, метод обратной матрицы, метод Гаусса.