3.3. Приведение системы сил к двум силам

Рассмотрим еще один способ приведения системы сил к простейшему виду.

Теорема. Произвольная пространственная система сил эквивалентна двум силам, которые в общем случае не лежат в одной плоскости.

Доказательство

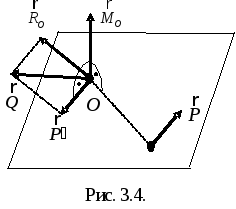Предположим, что произвольная система сил с помощью теоремы Пуансо приведена к силе, приложенной в центре приведенияO, и паре сил, момент которой (рис. 3.4). Выберем силы, образующие пару, так, чтобы

,

приложим силу в точкеO. Затем, воспользовавшись аксиомой параллелограмма сил, сложим силы и, в результате чего получим систему двух сил, в общем случае не лежащих в одной плоскости.

Итак,   ,

а значит теорема доказана.

3.4. Условия равновесия пространственной системы сил

Теорема. Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы относительно произвольного центра O равнялись нулю:

. (3.4)

Доказательство

Докажем необходимость условий (3.4). Предположим, что система сил уравновешена, и приведем ее к двум силам  0. Тогда в соответствии с 1-й аксиомой статики эти силы должны действовать вдоль одной прямой и . Так как, получим

, (3.5)

где , так как– пара сил и поэтому из формулы (3.5) следует, что. Так как силыинаправлены вдоль одной прямой, линия действия последней проходит через точкуO, в которой приложена сила (см. рис. 3.4), и поэтому главный момент

,

т.е. необходимость доказана.

Теперь докажем достаточность. Предположим, что и, тогда система сходящихся сил и система пар, полученные при доказательстве теоремы Пуансо, уравновешены. Следовательно, исходная система сил эквивалентна нулю. Теорема доказана.

Спроецируем векторные равенства (3.4) на оси координатной системы Oxyz и запишем

откуда с учетом (3.1) и (3.2) получим шесть уравнений равновесия пространственной системы сил:

(3.6)

Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на каждую из трех координатных осей и суммы их моментов относительно этих осей равнялись нулю.

3.5. Теорема Вариньона

Теорема. Если система сил имеет равнодействующую, то ее момент относительно произвольной точки равен сумме моментов всех сил системы относительной этой же точки.

Доказательство

Р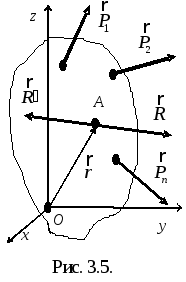ассмотрим систему сил, имеющую равнодействующую,приложенную в точке A (рис. 3.5). Приложим уравновешивающую силу в этой же точке и получим систему сил 0, главный момент которой относительно точки O

. (3.7)

Но

и поэтому из выражения (3.7) получим

,

откуда следует

, (3.8)

что и нужно было доказать.

Теорема Вариньона справедлива и для моментов сил относительно координатных осей. Действительно, спроецируем векторное равенство (3.8) на оси системы Oxyz и получим

. (3.9)

3.6. Условия равновесия плоской системы сил

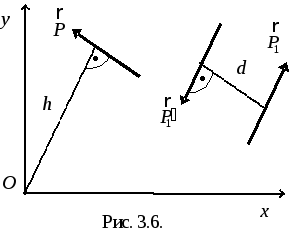Систему сил, линии действия которых лежат в одной плоскости, называют плоской. Пусть эта плоскость совпадает с координатной плоскостьюOxy (рис. 3.6). Тогда векторы моментов сил относительно любой точки плоскости и векторы моментов пар сил перпендикулярны плоскости действия сил и полностью определяются своими алгебраическими значениями.

Алгебраический момент силы относительно точки равен взятому с определенным знаком произведению модуля силы на ее плечо относительно точки

. (3.10)

Алгебраический момент пары сил равен взятому с определенным знаком произведению модуля одной из сил пары на ее плечо

. (3.11)

Знак «плюс» в формуле (3.10) берем в том случае, когда сила стремится повернуть тело вокруг точкиО против часовой стрелки, знак «минус» соответствует повороту по часовой стрелке. Аналогично определяют и знак момента в формуле (3.11). Введенные таким образом алгебраические моменты совпадают с моментами сил и пар относительно оси Oz, направленной к нам.

Условия равновесия плоской системы сил получим из уравнений (3.6). Так как все силы лежат в плоскости Oxy, их проекции на ось Oz и моменты относительной осей Ox и Oy равны нулю, поэтому 3, 4 и 5-е уравнения выполняются тождественно. Оставшиеся уравнения, используя введенные алгебраические моменты, запишем так:

. (3.12)

Таким образом, для равновесия плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на две координатные оси и сумма алгебраических моментов всех сил относительно произвольной точки плоскости их действия равнялись нулю.

Пример 1. На раму AB (рис. 3.7,а) действуют сила F = 2 кН и пара сил, момент которой M = 1 кНм.

Определить реакции опор.

Рассмотрим равновесие рамы AB, которую освободим от связей, заменив их действие реакциями (рис. 3.7,б): – составляющие реакции неподвижного цилиндрического шарнираA; – реакция подвижного цилиндрического шарнираB, направленная перпендикулярно опорной плоскости.

Разложим силы ина составляющие, параллельные координатным осям:

кН; кН;

.

Пара сил задана величиной момента и направлением действия.

Для полученной плоской системы сил запишем три уравнения равновесия:

При составлении уравнений равновесия целесообразно координатные оси направить перпендикулярно неизвестным силам, а моменты сил вычислять относительно точек пересечения линий действия неизвестных сил, что обеспечит получение наиболее простых уравнений, содержащих минимальное число неизвестных. Из уравнений равновесия получим

кН;

кН;

.

Для проверки правильности решения рассмотрим условие равновесия, не использованное при решении примера. Выберем точку, относительно которой все найденные реакции имеют моменты (точка D, см. рис. 3.7,б), и вычислим сумму моментов всех действующих на раму сил относительно этой точки:

.

Условие равновесия выполнено.

Ответ:

Отрицательные значения реакций показывают, что действительные направления сил ипротивоположны первоначально выбранным (см. рис. 3.7,б).

Пример 2. На консольную балку AB, показанную на рис. 3.8,а, действуют сила Р = 1 кН, пара сил, момент которой M = 3 кНм, и равномерно распределенная нагрузка интенсивностью q = 2 кН/м.

Определить реакцию жесткой заделки А.

В этом примере используем не рассматривавшуюся ранее связь, называемую жесткой заделкой. Она препятствует перемещению точки А и повороту балки вокруг этой точки. На закрепленный конец балки действует распределенная система реактивных сил, которую можно привести к силе, приложенной в точке А, и паре сил. Представим силу составляющими ,, а момент пары обозначим через.

Таким образом, освобождая балку от связи, покажем три составляющие реакции жесткой заделки: ,,(рис. 3.8,б). Равномерно распределенную нагрузку заменим ее равнодействующей, приложенной в середине нагруженного участка,кН. Итак, на балку действует плоская система сил и пар сил. Запишем три уравнения равновесия этой системы:

из которых получим

= P = 1 кН; = 6 кН;

= 21 + 4,56  3 = 26 кНм.

Для проверки правильности решения вычислим сумму моментов всех сил, действующих на балку, относительно точки В

.

Ответ: .