Фкпоу «нтти» Минтруда России
Экзаменационный билет № |
9 |
Дисциплина |
Теория алгоритмов |
Специальность |
09.02.03 |
Группы |
П-1С, П-2 |
1.Алгоритмы табулирования функции.
2.Сортировка методом простого включения
3. Задача 1. Для данного вещественного x найти значение следующей функции f, принимающей вещественные значения:
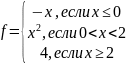
Определите временную сложность алгоритма
4. Задача 2. Дан двумерный массив из NхM (N,M<25) элементов целого типа. Определить наибольший элемент массива и сколько раз он встречается в массиве. Определите временную сложность алгоритма
Преподаватель Каныгин Д.Г.
Фкпоу «нтти» Минтруда России
Экзаменационный билет № |
10 |
|
Дисциплина |
Теория алгоритмов |
|
Специальность |
09.02.03 |
|
Группы |
П-1С, П-2 |
|
1. Алгоритмы нахождение сумм числовых последовательностей с заданной погрешностью.
2. Алгоритмы быстрой сортировки.Сортировка методом Шелла
3. Задача 1.Для данного вещественного x найти значение следующей функции f, принимающей значения целого типа:
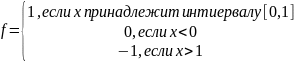
Определите временную сложность алгоритма
4. Задача 2.Составить алгоритм и программу вычисления таблицы значений функции f=sin(x) для N значений аргумента X, равномерно распределенных на отрезке [A,B]. Определите временную сложность алгоритма
Преподаватель Каныгин Д.Г.
Фкпоу «нтти» Минтруда России
Экзаменационный билет № |
11 |
Дисциплина |
Теория алгоритмов |
Специальность |
09.02.03 |
Группы |
П-1С, П-2 |
1. Алгоритмы с использованием циклов с параметром.
2.Анализ сложности рекурсивных алгоритмов
3. Задача 1. Дан номер года (положительное целое число). Определить количество дней в этом году, учитывая, что обычный год насчитывает 365 дней, а високосный — 366 дней. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400 (например, годы 300, 1300 и 1900 не являются високосными, а 1200 и 2000 — являются). Определите временную сложность алгоритма
4. Задача 2. Составить алгоритм и программу вычисления таблицы значений функции f=tg(x) для N значений аргумента X, равномерно распределенных на отрезке [A,B]. Учесть ОДЗ. Определите временную сложность алгоритма
Преподаватель Каныгин Д.Г.
Фкпоу «нтти» Минтруда России
Экзаменационный билет № |
12 |
|
Дисциплина |
Теория алгоритмов |
|
Специальность |
09.02.03 |
|
Группы |
П-1С, П-2 |
|
1. Принципы построения сложных алгоритмов. Структурная методика алгоритмизации. Метод последовательной детализации.
2. Оптимизация алгоритмов
3. Задача 1.Дано целое число. Вывести его строку-число вида 1- если число «отрицательное четное число», 2- «нулевое число», 3-«положительное нечетное число», 4 - число положительное четное, 5- число отрицательное нечетное. Определите временную сложность алгоритма
4. Задача 2.Даны два натуральных числа A и B. Требуется найти их наибольший общий делитель (НОД). Определите временную сложность алгоритма
Преподаватель Каныгин Д.Г.