
- •В.М. Адашевский, г.О. Анищенко, ю.Л. Тарсис теоретическая механика статика
- •Рецензенти: Ольшансский в.П., професор кафедри прикладної механіки Академії цивільного захисту України, д-р фіз.-мат. Наук;
- •Введение
- •1. Основные положения статики
- •Понятия и определения
- •1.2. Типы связей и их реакции
- •1.2.4. Цилиндрическая шарнирно-подвижная опора
- •1.3. Условия равновесия твердого тела
- •1.4. Центр параллельных сил. Центр тяжести
- •2. Равновесие тела под действием пространственной системы сходящихся сил
- •2.1. Краткие теоретические сведения
- •2.2. Последовательность решения задач
- •2.3. Примеры решения типовых задач
- •Решение
- •Решение
- •3. Равновесие тела под действием произвольной плоской системы сил
- •3.1. Краткие теоретические сведения
- •3.2. Примеры решения типовых задач
- •Решение
- •Решение
- •Решение
- •4. Равновесие тела под действием произвольной пространственной системы сил
- •4.1. Краткие теоретические сведения
- •4.2. Примеры решения типовых задач
- •Решение
- •Решение
- •Решение
- •Вопросы для самоконтроля
- •5. Задания к контрольным работам
- •Задание № 1 Равновесие пространственной системы сходящихся сил
- •Задание № 2 Равновесие произвольной плоской системы сил
- •Задание № 3 Равновесие произвольной пространственной системы сил
- •Список рекомендуемой ЛитературЫ
- •Содержание
- •Теоретична механіка статика
- •61002, Харків, вул. Фрунзе, 21
2.3. Примеры решения типовых задач
Приведем несколько типичных примеров решения задач.
Пример 1.На столбАО(идеальный
стержень) высотой 6 м, укрепленный
оттяжкамиАСиAD, которые
симметрично расположены относительно
плоскостиyOz(рис. 2.2), действует сила
натяжения проводаT= 300 H, которая
направлена параллельно осиy. При
этом![]() =
1200, аОС=ОD= 4,5 м.
=
1200, аОС=ОD= 4,5 м.
Определить натяжения тросов в оттяжках и усилие, действующее на столб.

Решение
1) В качестве объекта равновесия примем точку А.
2) Активной силой является сила натяжения
![]() проводаАВ.
проводаАВ.
3) Отбрасывая связи (оттяжки АD,ACи столбAO), заменим их действие на
объект равновесия реакциями![]() и
и![]() .
.
4) Запишем уравнения равновесия (2.3)
полученной системы сходящихся сил в
принятой системе координат (см. рис.
2.2). Для удобства составим табл. 2.1, которая
является вспомогательной, а для сил
![]() и
и![]() применим способ двойного проецирования.
применим способ двойного проецирования.
Таблица 2.1
|
|
|
|
|
|
|
Fkx |
0 |
|
|
0 |
|
Fky |
T |
|
|
0 |
|
Fkz |
0 |
|
|
– N |
Теперь для записи системы уравнений равновесия просуммируем элементы соответствующих строк таблицы и приравняем эти суммы нулю:
![]()
![]() =
0;
=
0;
T![]()
![]() =
0;
=
0;
![]()
![]() –N = 0.
–N = 0.
Здесь
![]()
Из 1-го уравнения полученной системы
следует, что![]() .
Далее находим:
.
Далее находим:
из 2-го уравнения
![]() Н,
Н,
из 3-го уравнения
![]() Н.
Н.
Знак «минус» указывает на то, что реакция столба в действительности направлена в сторону, противоположную принятой (см. рис. 2.2).
Пример 2.ГрузQвесом 100 кН с помощью троса, переброшенного через неподвижный блокЕ, прикреплен к точкеDи удерживается в равновесии тремя идеальными стержнями, которые шарнирно присоединены к этой точке (рис. 2.3).
Определить усилия в стержнях AD,BDиCD, если α = 450, β = 600, γ = 300, ε = 300. Трением в блоке пренебречь.

Решение
1) В качестве объекта равновесия примем точку D.
2) Активной силой является сила
![]() натяжения нити, действующая на объект
равновесия, причем величина этой силы
равна весу грузаQ, поскольку трение
в блоке отсутствует.
натяжения нити, действующая на объект
равновесия, причем величина этой силы
равна весу грузаQ, поскольку трение
в блоке отсутствует.
3) Реакции связей, усилия в идеальных
стержнях
![]() и оси выбранной системы координат
показаны на схеме (см. рис. 2.3).
и оси выбранной системы координат
показаны на схеме (см. рис. 2.3).
4) Запишем уравнения равновесия, в данном случае не составляя вспомогательной таблицы:
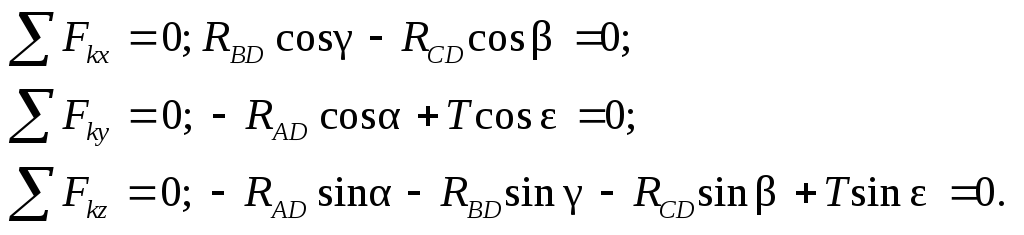
Вначале решаем 2-е уравнение, поскольку в нем содержится одна неизвестная реакция
![]() кН.
кН.
Затем, выражая из 1-го уравнения
![]() и подставляя
и подставляя![]() и
и![]() в 3-е уравнение
в 3-е уравнение
![]() ,
,
находим
![]() кН.
кН.
Далее определяем
![]() кН.
кН.
Знаки «минус» у реакций
![]() и
и![]() означают, что эти силы имеют направления,
противоположные указанным на рис. 2.3.
означают, что эти силы имеют направления,
противоположные указанным на рис. 2.3.
Пример 3.В крановой конструкции грузQвесом 500 кН, прикрепленный к вертикальной стене в точкеОс помощью троса, переброшенного через блокG, удерживается в равновесии тремя идеальными стержнями, одни концы которых шарнирно соединены в точкеD, а другие прикреплены с помощью шарниров к той же стене (рис. 2.4,а).
Определить усилия в стержнях, если α = β = 450, γ = 600, ε = 300. Размерами блока и трением пренебречь.

Решение
1) В качестве объекта равновесия примем точку D.
2) Активные силы, действующие на объект
равновесия, приведены на схеме (см. рис.
2.4,б). Учитывая, что трение в блоке
отсутствует, активными силами будут
силы
![]() и
и![]() ,
равные по величине силе тяжести грузаQ.
,
равные по величине силе тяжести грузаQ.
3) Реакции связей – усилия в идеальных
стержнях
![]()
![]() – направлены от узлаD(см. рис.
2.4,б).
– направлены от узлаD(см. рис.
2.4,б).
4) Запишем уравнения равновесия:
![]()
![]()
Из 2-го уравнения следует, что![]() ,
а поскольку
,
а поскольку![]() ,
то
,
то![]() .
Далее из 3-го уравнения находим
.
Далее из 3-го уравнения находим
![]()
и подставляем в 1-е, откуда, учитывая,
что![]() ,
определяем
,
определяем
![]()
![]() кН.
кН.
а затем
![]() кН.
кН.
Таким образом, имеем
![]() кН
и
кН
и![]() кН.
кН.
Знак «минус» у реакций
![]() и
и![]() означает, что направления этих сил
противоположны принятым (см. рис. 2.4,б).
означает, что направления этих сил
противоположны принятым (см. рис. 2.4,б).
Вопросы для самоконтроля
1. Какая совокупность сил называют системой сходящихся сил?
2. Как сформулировать условие равновесия системы сходящихся сил в векторной форме?
3. Как записать аналитические условия равновесия системы сходящихся сил?
4. Как определяют проекцию силы на ось?
5. В чем заключается способ двойного проецирования вектора?
6. В какой последовательности следует решать задачу об определении реакций связей из условия равновесия тела?
7. Какой вывод следует сделать, если реакции некоторых связей оказались со знаком «минус»?
