4.2. Примеры решения типовых задач

Пример 1.Определить из условий равновесия реакции подпятникаA, неподвижного цилиндрического шарнираBи величину силыдля невесомого вертикального валаAB(рис. 3.2), к которому жестко прикреплены стержниCDиKE, расположенные в плоскостях, перпендикулярных осиz, причем стерженьCDпараллелен осиx, а стерженьKE– осиy. Конструкция нагружена силамии, причем сила,кН расположена в плоскости, перпендикулярной осиz, и составляет с осью стержняKEугол γ = 30⁰, а сила– в плоскости, перпендикулярной осиx, и составляет с горизонталью угол β = 60⁰. Кроме того, к концам стержняLG, жестко прикрепленного к валу и расположенного в плоскостиyOz, приложены две равные, противоположно направленные силыи, параллельные осиxи образующие пару сил. Вектор-момент этой парыкН·м расположен в плоскостиyOzи составляет с осьюz угол α = 30⁰. Размеры на схеме даны в метрах.

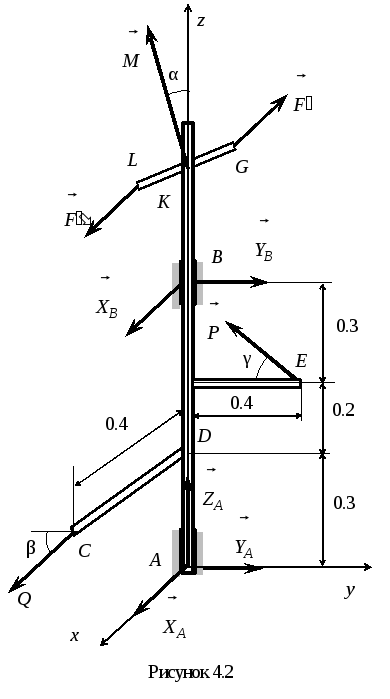
Решение

1) Объектом равновесия является вся конструкция (вал с прикрепленными к нему стержнями).

2) Активными силами, действующими на объект равновесия, будут силы,и пара сил, вектор-момент которой.

3) Отбрасывая связи (подпятник A и неподвижный цилиндрический шарнирB), заменим их действие на объект равновесия реакциямии. Реакция подпятника представлена составляющими,и, а неподвижного цилиндрического шарнира – составляющимии, параллельными соответствующим координатным осям.

4) Запишем уравнения равновесия (4.4) полученной пространственной системы сил в принятой системе координат (см. рис. 4.2) с помощью табл. 4.1.

Таблица 4.1

		0	0		0
	0		0	0
	0	0		0	0
	0	0	0	0
	0	0	0		0
	0	0	0	0	0

Продолжение табл. 4.1

	0		–
			–
		0	–
			0

Рассмотрим более подробно определение момента силы относительно оси на примере силы (см. рис. 4.2).

Способ 1. Определим проекции силы:

– на плоскость, перпендикулярную оси x,

– на плоскость, перпендикулярную оси y,

– на плоскость, перпендикулярную оси z,

При определении моментов силы относительно осейxиyплечом будет одно и то же расстояниеAK. Поэтому с учетом знаков получим

При определении моментов силы относительно осиzучтем, что сила уже расположена в плоскости, перпендикулярной этой оси. Точка пересечения этой плоскости с осью – это точкаК. Для нахождения алгебраического момента силыотносительно этой точки воспользуемся теоремой Вариньона

Способ 2. Запишем проекции силына оси координат:

и координаты точки приложения силы – точкиE:

Используя аналитические выражения (4.2), получим

Cуммируя элементы соответствующих строк таблицы и приравнивая эти суммы нулю, получим систему уравнений равновесия:

5) Решим полученную систему, начиная с уравнений, содержащих не более одной неизвестной силы. Так, из последнего уравнения определим

Затем с учетом найденного значения Qрешим 5-е уравнение и определим

Далее из уравнений находим:

из 1-го

из 3-го

из 4-го

и, наконец, из 2-го

Пример 2.Определить реакции жесткой пространственной заделкиАдля невесомой рамыABC(рис. 4.3.), расположенной в горизонтальной плоскостиxOyи нагруженной силой,силамии, образующими пару сил, вектор-момент которой,. Кроме того, с помощью троса, переброшенного через неподвижный блокDи прикрепленного к концуСрамы, удерживается в равновесии груз весом= 2 кН. Силарасположена в плоскости, перпендикулярной осиy, и составляет с прямойBCугол α = 30⁰ . СтерженьKE, к концам которого приложены силы пары, параллельные осиx, жестко прикреплен к раме и расположен в плоскостиyOzпод углом β = 60⁰ к осиy. ПрямаяCDпараллельна осиx. Размеры на схеме даны в метрах.